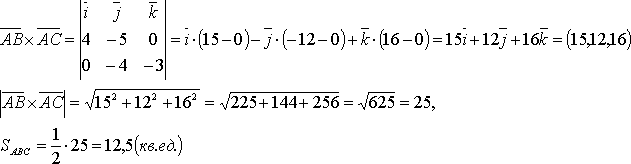- •2. Миноры и алгебраические дополнения. Разложение определителя по элементам произвольного ряда.
- •3. Матрицы и их свойства. Ранг матрицы.
- •4. Операции над матрицами, обратная матрица.
- •5. Решение и исследование систем линейных неоднородных алгебраических уравнений с помощью формул Крамера.
- •6. Решение системы линейчатых неоднородных алгебраических уравнений средствами матричного исчисления.
- •7. Метод Гаусса решения систем линейных неоднородных алгебраических уравнений. Теорема Кронекера-Капелли.
- •Доказательство (условия совместности системы)
- •9. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами и их основные свойства. Линейные операции над векторами Сложение векторов
- •Вычитание векторов
- •Умножение вектора на число
- •Свойства линейных операций над векторами
- •Линейные комбинации векторов
- •11. Теоремы о проекциях векторов. Условие коллинеарности векторов.
- •Условия коллинеарности векторов
- •12. Линейная зависимость векторов. Понятие базиса.
- •Свойства линейно зависимых и линейно независимых векторов
- •Пример.
- •13. Скалярное произведение векторов. Признак ортогональности векторов.
- •14. Расстояние между двумя точками пространства r3 . Деление отрезка в данном отношении. Расстояние между точками в пространстве, формула.
- •Вывод формул для нахождения координат точки, делящей отрезок в данном отношении, на плоскости.
- •15. Векторное произведение векторов.
- •16. Смешанное произведение векторов. Условие компланарности векторов.
- •17. Метод координат и основные задачи аналитической геометрии.
- •18. Прямые в r2. Различные виды уравнений прямой в r2
- •19. Нормированное уравнение прямой.
- •20. Условия параллельности и перпендикулярности прямых. Вычисление угла между прямыми в r2.
- •21. Расстояние от точки до прямой в r2.
- •22. Линии второго порядка. Каноническое уравнение окружности.
- •23. Каноническое уравнение эллипса.
- •24. Каноническое уравнение гиперболы.
- •25. Каноническое уравнение параболы.
- •26. Преобразование уравнений линий второго порядка к каноническому виду. Параллельный перенос системы координат.
- •28. Параметрическая форма задания уравнения линий в трехмерном пространстве.
- •29. Плоскость в трехмерном пространстве. Различные виды уравнений плоскости.
- •30. Нормированное уравнение плоскости
- •31. Расстояние от точки до плоскости.
- •32. Расстояние между двумя параллельными прямыми.
- •33. Прямая в пространстве. Различные формы уравнения прямой.
- •34. Угол между двумя пересекающимися прямыми в пространстве. Расстояние от точки до прямой в пространстве.
- •Первый способ нахождения расстояния от точки до прямой a в пространстве.
- •Второй способ, позволяющий находить расстояние от точки до прямой a в пространстве.
- •35. Расстояние между перекрещивающимися прямыми в пространстве.
- •Нахождение общего перпендикуляра скрещивающихся прямых.
- •36. Поверхности второго порядка. Эллипсоиды и гиперболоиды.
- •37. Параболоиды. Уравнения цилиндрических и конических поверхностей.
- •38. Сферическая система координат.
Вывод формул для нахождения координат точки, делящей отрезок в данном отношении, на плоскости.
Начнем с постановки задачи на плоскости.
Пусть
на плоскости введена прямоугольная
декартова система координат Oxy и
заданы координаты двух несовпадающих
точек ![]() и
и ![]() .
Нам требуется найти координаты
.
Нам требуется найти координаты ![]() и
и ![]() точки С,
которая делит отрезок АВ в
отношении
точки С,
которая делит отрезок АВ в
отношении ![]() ,
где
,
где ![]() -
некоторое положительное действительное
число.
-
некоторое положительное действительное
число.
Поясним
смысл фразы: «точка С делит
отрезок АВ в
отношении ![]() ».
Это выражение означает, что точка С лежит
на отрезке АВ (является
внутренней точкой отрезка АВ)
и отношение длин отрезков АС и СВ равно
».
Это выражение означает, что точка С лежит
на отрезке АВ (является
внутренней точкой отрезка АВ)
и отношение длин отрезков АС и СВ равно ![]() (то
есть, выполняется равенство
(то
есть, выполняется равенство 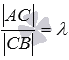 ).
Обратите внимание, что в этом случае
точка А является
как бы началом отрезка, а точка В –
его концом. Если же сказано, что
точка С делит
отрезок ВА (а
не АВ)
в отношении
).
Обратите внимание, что в этом случае
точка А является
как бы началом отрезка, а точка В –
его концом. Если же сказано, что
точка С делит
отрезок ВА (а
не АВ)
в отношении ![]() ,
то будет выполняться равенство
,
то будет выполняться равенство 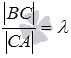 .
Очевидно, что при
.
Очевидно, что при ![]() точка С является
серединой отрезка АВ.
точка С является
серединой отрезка АВ.
Поставленная задача может быть решена с помощью векторов.
Изобразим
в прямоугольной декартовой системе
координат некоторый отрезок АВ,
точку С на
нем и построим радиус-векторы
точек А, В и С,
а также векторы ![]() и
и ![]() .
Будем считать, что точка С делит
отрезок АВ в
отношении
.
Будем считать, что точка С делит
отрезок АВ в
отношении ![]() .
.
Мы
знаем, что координаты
радиус-вектора точки
равны соответствующим координатам этой
точки, поэтому, ![]() и
и ![]() .
Найдем координаты вектора
.
Найдем координаты вектора ![]() ,
которые будут равны искомым координатам
точки С,
делящей отрезок АВ в
заданном отношении
,
которые будут равны искомым координатам
точки С,
делящей отрезок АВ в
заданном отношении ![]() .
.
В
силу операции
сложения векторов можно
записать равенства ![]() и
и ![]() .
Их мы используем в следующем абзаце.
.
Их мы используем в следующем абзаце.
Так
как точка С делит
отрезок АВ в
соотношении ![]() ,
то
,
то 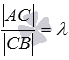 ,
откуда
,
откуда ![]() .
Векторы
.
Векторы ![]() и
и ![]() лежат
на одной прямой и имеют одинаковое
направление, а выше мы отметили, что
лежат
на одной прямой и имеют одинаковое
направление, а выше мы отметили, что ![]() ,
поэтому, по определению
операции умножения вектора на числосправедливо равенство
,
поэтому, по определению
операции умножения вектора на числосправедливо равенство ![]() .
Подставив в него
.
Подставив в него ![]() ,
имеем
,
имеем 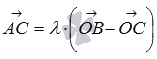 .
Тогда равенство
.
Тогда равенство ![]() можно
переписать как
можно
переписать как  ,
откуда в силу свойств
операций над векторами получаем
,
откуда в силу свойств
операций над векторами получаем  .
.
Осталось
вычислить координаты вектора 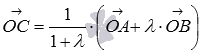 ,
выполнив необходимые операции
над векторами
,
выполнив необходимые операции
над векторами ![]() и
и ![]() в
координатах.
Так как
в
координатах.
Так как ![]() и
и ![]() ,
то
,
то ![]() ,
следовательно,
,
следовательно, 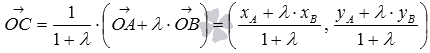 .
.
Таким
образом, на плоскости координаты
точки С,
которая делит отрезок АВ в
отношении ![]() ,
находятся по формулам
,
находятся по формулам 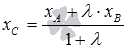 и
и 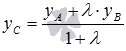 .
.
15. Векторное произведение векторов.
Векторное проведение векторов.
Определение:
Под векторным произведением двух
векторов ![]() и
и ![]() понимается
вектор,
понимается
вектор, ![]() для
которого:
для
которого:
-модуль
равен площади параллелограмма,
построенного на данных векторах, т.е. ![]() ,
где
,
где ![]() угол
между векторами
угол
между векторами ![]() и
и ![]()
-этот
вектор перпендикулярен перемножаемым
векторам, т.е. ![]()
-если
векторы ![]() неколлинеарны,
то они образуют правую тройку векторов.
неколлинеарны,
то они образуют правую тройку векторов.
Свойства векторного произведения:
1.При
изменении порядка сомножителей векторное
произведение меняет свой знак на
обратный, сохраняя модуль, т.е. ![]()
2.Векторный
квадрат равен нуль-вектору, т.е. ![]()
3.Скалярный
множитель можно выносить за знак
векторного произведения, т.е. ![]()
4.Для
любых трех векторов ![]() справедливо
равенство
справедливо
равенство ![]()
5.Необходимое
и достаточное условие коллинеарности
двух векторов ![]() и
и ![]() :
: ![]()
Векторное произведение в координатной форме.
Если
известны координаты векторов ![]() и
и ![]() , то
их векторное произведение находится
по формуле:
, то
их векторное произведение находится
по формуле:
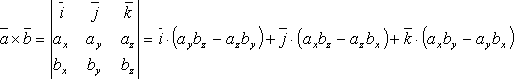 .
.
Тогда
из определения векторного произведения
следует, что площадь параллелограмма,
построенного на векторах ![]() и
и ![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]()
Пример: Вычислить
площадь треугольника с
вершинами ![]() (1;-1;2),
(1;-1;2), ![]() (5;-6;2),
(5;-6;2), ![]() (1;3;-1).
(1;3;-1).
Решение: 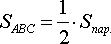 .
.
![]() ,
, ![]() ,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
,
тогда площадь треугольника АВС будет
вычисляться следующим образом:
![]() ,
,
![]()