Розділ 1 Основи теорії множин

У розділі висвітлено зміст основних понять теорії множин і показано їх практичне застосування при виконанні операцій над множинами.

§ 1.1. Основні поняття

Засновник теорії множин Г. Кантор дав таке визначення її базового поняття: множина – це сукупність елементів, що розглядаються як єдине ціле. Задати множину можна або простим переліком її елементів, або назвавши ознаку, яка властива всім її елементам. Наприклад:

, .

Тут множину Х задано переліком елементів, а множину Y – зазначенням властивості елементів.

Запис означає, що елемент належить множині. Символомпозначаєтьсяпорожня множина, яка не містить жодного елемента.

Будь-який набір елементів, кожний з яких належить множині називаєтьсяпідмножиною множини

Наприклад, нехай , тоді множина А являє собою підмножину множини _.

Запис: означає, що підмножина А міститься в множині Х. За визначенням кожна множина є підмножиною самої себе, тобто . Крім того,. Таким чином, кожна підмножина має принаймні дві підмножини: порожню множину і саму себе.

Якщо множина Х складається з елементів, то завжди існує 2ⁿ її підмножин. Наприклад, коли множина , тобто, то існує така кількість її підмножин: 2³ = 8, а саме: .

Множина, яка містить усі елементи, розглянуті в дискретній математиці, називається універсальною множиною . Очевидно, що будь-яка множина являє собою підмножину універсальної множини , тобто.

Для наочного зображення співвідношень між множинами використовуються діаграми Ейлера. Вони зображують універсальну множину у вигляді прямокутника, усередині якого розміщуються інші множини, їх зображують у вигляді кіл (див. рис. 1.1).

S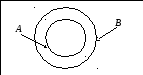

Рис. 1.1. Приклад діаграми Ейлера

Нагадаємо загальноприйняті позначення числових множин, які відіграють важливу роль у теорії множин:

–множина натуральних чисел;

– множина цілих чисел;

–множина раціональних чисел;

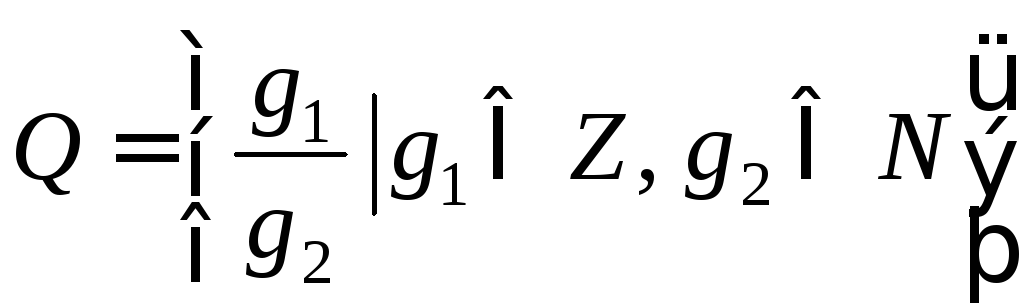– множина дійсних чисел відрізка , часто;.

Очевидно, що .

Множина, що містить скінченну кількість елементів, називається скінченною. Множина, що не є скінченною, називається нескінченною.

Будь-яка множина має важливу універсальну характеристику – потужність множини (кардинальне число). Вона позначається таким чином:.

Потужність скінченних множин дорівнює кількості елементів множини. Наприклад: множина , тоді.

Кардинальні числа мають місце також і для нескінченних множин. Так, Г. Кантор запропонував позначити потужність множини натуральних чисел символом (читається якалеф-нуль), тобто .

Г. Кантор сформулював також принцип порівняння потужностей двох множин: якщо між елементами двох множин можна встановити взаємно однозначну відповідність, то ці множини рівнопотужні. Наприклад, нехай дано множини: та. Взаємно однозначну відповідність між ними встановлено таким чином:

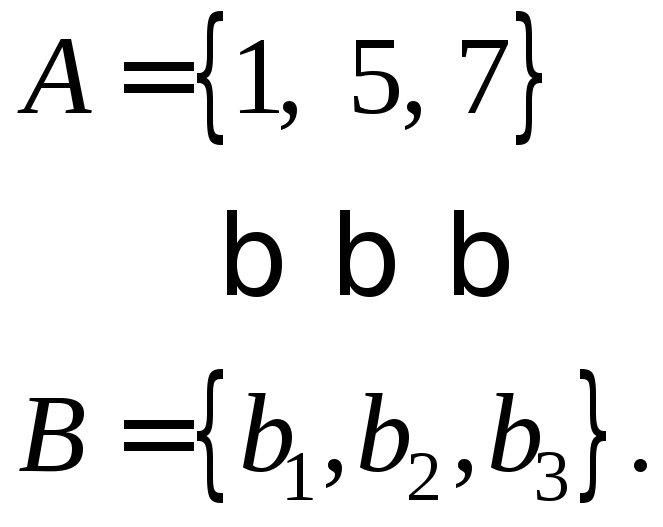
Зрозуміло, що , тобто ці множини рівнопотужні.

Сформульований принцип можна також застосовувати для порівняння потужностей нескінченних множин.

Наприклад: , це множина парних натуральних чисел. Очевидно, що, однак, ми можемо встановити відповідність між цими множинами таким чином:

а це означає, що .

Аналогічно можна показати, що .

Усі множини, які рівнопотужні множині натуральних чисел N, називаються лічильними й мають потужність .

Існують нескінченні множини, які не можна поставити у відповідність натуральному ряду чисел, наприклад, множина дійсних чисел R. Такі множини обумовлені поняттям «неперервність» і мають потужність континууму (позначається c) й називаються континуальними.