
Сербо В. Г. Лекции по физике элементарных частиц
.pdf
61
B. Уравнение Клейна Фока Гордона (КФГ)
В релятивистской теории операторы
i~ ∂
pˆ0 = c ∂t è pˆ = −i~r
образуют 4-мерный вектор
|
pˆµ = i~ |
|
1 ∂ |
, −r ≡ i~∂µ. |
|
|||||||
|
|
|
|
|
|
|||||||
|
|
c ∂t |
|
|||||||||
Уравнение Шр¼дингера |
Ψ(t, r) = 2m pˆ |
− cA + eφ |
|
|||||||||
cpˆ0 |
Ψ(t, r) |
|||||||||||
|
|
|
1 |
|
|
|
e |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
||||
и уравнение Паули
cpˆ0 Ψ(t, r) = |
2m σ pˆ |
− cA |
|
|
|
1 |
|
e |
2 |
+ eφ Ψ(t, r)
не является релятивистски ковариантными уравнениями, компоненты pˆµ входят в них явно несимметричным образом: эти уравнения содержат первые степени оператора pˆ0 и вторые степени оператора pˆ. Простейшие релятивистские обобщения этих уравнений можно получить двумя способами:
1)потребовав, чтобы в уравнение входила вторая степень оператора pˆ0 (â ýòîì ñëó- чае мы прийд¼м к уравнению Клейна Фока Гордона);
2)потребовав, чтобы в уравнение входила первая степень оператора pˆ (в этом случае
мы прийд¼м к уравнению Дирака).
Классическое соотношение для компонент 4-импульса релятивистской частицы 5
|
e |
µ |
e |
|
|||
p − |
|
A |
|
p − |
|
A µ |
= m2c2 , |
c |
|
c |
|||||
ãäå Aµ = (A0(t, r), A(t, r)) 4-потенциал электромагнитного поля и A0(t, r) ≡ φ(t, r)
скалярный потенциал, соответствует релятивистскому волновому |
уравнению Клейна |
||||||||
Фока Гордона (1926 |
− 1927 ã.) |
|
− −i~r − cA # Ψ(t, r) = m2c2 |
|
|
|
|||
" i c |
∂t − c A0 |
2 |
Ψ(t, r) . |
(B.1) |
|||||
~ |
|
|
e |
|
e |
2 |
|
|
|
Cвободному движению частицы с определенным 4-импульсом |
pµ = (E/c, p) ñîîò- |
||||||||
ветствует плоская волна |
|
|
|
|
|
|
|||
|
|
|
Ψ(x) = N e−i(Et−pr)/~ = N e−ipµxµ/~ . |
|
|
(B.2a) |
|||
5Здесь и ниже по повторяющимся индексам 4-векторов подразумевается суммирование, т. е. выражение AµBµ означает AµBµ ≡ A0B0 − AxBx − AyBy − AzBz = A0B0 − AB. Мы нередко будем
использовать сокращенное обозначение AB ≡ AµBµ.

62
Если подставить эту волновую функцию в уравнение (1) с Aµ = 0, то найдем естественную связь между энергией и импульсом
E2 = m2c4 + p2c2 ,
которой соответствует закон дисперсии, т. е. зависимость энергии от импульса, вида
p
E(p) = ±εp , εp = +c m2c2 + p2 .
Отложим обсуждение двух возможных знаков ± в этом выражении до D.
Релятивистское уравнение КФГ оказалось уравнением второго порядка по времени. Это приводит к следующему принципиальному отличию от нерелятивистской квантовой механике, основанной на уравнении Шр¼дингера уравнении первого порядка по времени. Один из постулатов квантовой механики интерпретация квадрата модуля волновой функции как плотности вероятности:
ρ(r, t) = Ψ(r, t) Ψ(r, t) .
Эта плотность вероятности и плотность тока вероятности
|
1 |
|
|
|
e |
|
||
j = |
|
Ψ |
−i~r − |
|
A Ψ + êîìï. cîïð. |
(B.3) |
||
2m |
c |
|||||||
связаны уравнением непрерывности |
|
|
|
|
||||
|
|
|
|
∂% |
+ rj = 0 , |
(B.4) |
||
|
|
|
|
|
||||
|
|
|
|
∂t |
||||
из которого следует, что условие нормировки
Z
ρ(r, t) d3r = 1
не изменяется с течением времени.
Подобная интерпретация невозможна для волновой функции уравнения КФГ, так как для не¼ интеграл R Ψ(r, t) Ψ(r, t) d3r не сохраняется с течением времени. Естествен-
ным релятивистским обобщением 3-вектора (3) является 4-вектор
jµ = nΨ |
i~∂µ − cAµ |
Ψ + |
i~∂µ Ψ − cAµΨ |
· Ψo . |
(B.5) |
||
|
|
e |
|
|
e |
|
|
Легко проверит, используя уравнение КФГ, что компоненты этого 4-вектора удовлетворяют уравнению непрерывности
∂µjµ = 0 , |
(B.6) |
эквивалентному уравнению (4). Это означает, что роль плотности вероятности должна играть нулевая компонента вектора jµ, ò. å.6
ρ = c0 |
= c nΨ i~∂0 |
− cA0 |
Ψ + |
i~∂0 |
Ψ − cA0Ψ |
· Ψo . |
(B.7) |
|||
|
j |
1 |
|
e |
|
|
|
e |
|
|
6Для плоской волны (2a) с энергией E(p) = +εp плотность вероятности ρ = 2εp|N|2, поэтому при нормировке на одну частицу в объ¼ме V,
Z
ρ d3r = 2εp|N|2 V = 1 ,
V
амплитуда плоской волны равна |
|
|
|
|
|
1 |
|
|
|
||
N ≡ Np = |
|
|
|
. |
(B.2b) |
p |
|
|
|||
2εpV |
|||||

63
Однако эта величина не является положительно определ¼нной! Мы покажем ниже, что в квантовой теории поля 4-вектор jµ играет роль не плотности тока вероятности, но
плотности тока заряженных частиц, а в этом случае j0 величиной.
Уравнение КФГ и 4-вектор зования
Aµ → Aµ − ∂µf(x), Ψ → Ψ eief(x)/~c , |
(B.8) |
ãäå f(x) произвольная функция x = (ct, r).
Обсудим нерелятивистский предел p2 m2c2 уравнения КФГ. В этом случае
E = mc2 + p2 − (p2)2 + . . . .
2m 8m3c2
Рассмотрим движение нерелятивистской частицы в потенциальном поле U(r). Релятивистская поправка к нерелятивистскому оператору Гамильтона
ˆ |
|
pˆ2 |
|
H0 |
= |
|
+ U(r) |
2m |
|||
возникает из-за изменения закона дисперсии. Соответствующее возмущение равно
ˆ |
(pˆ2)2 |
|
V = − |
|
. |
8m3c2 |
||
В кулоновской задаче (при U(r) = −e2/r ) эта поправка снимает вырождение по l в спектре и приводит к тонкой структуре уровней. Возникающая поправка к энергии
|
|
Enl = hnl| Vˆ |nli = −2mc2 *nl 2m |
nl+ |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
pˆ2 |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
может быть переписана с учетом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
pˆ2 |
|
|
ˆ |
|
|
e2 |
|
|
ˆ |
|nl i = En |nl i |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2m |
|
= H0 |
+ |
|
r |
, H0 |
|
|
|
|
|
|
|||||||||||||||||
â âèäå |
−2mc2 |
* |
|
|
|
|
|
r |
|
+ |
|
− 2~2 n3 |
l + 21 − 4n |
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
e2 |
2 |
|
|
|
|
|
|
me4 α2 |
1 |
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Enl = |
|
|
|
nl |
|
En |
+ |
|
|
|
|
|
nl |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
. |
(B.9) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 3 |
|
|
|
|
|||||||||
|
|
l = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
l = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
l = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} n = 1 |
|
|
|
|
|||||||||
Тонкая структура уровней атома водорода согласно (B.9).

64
Здесь
α = e2 ≈ 1
~c 137
безразмерная константа, постоянная тонкой структуры. Однако реальный спектр атома водорода отличается от этого спектра. Причина в том, что уравнение КФГ не учитывает спин электрона.
C. Уравнение Дирака
C.1. Симметричная форма уравнения Дирака
В нерелятивистской квантовой механике спин электрона учитывается в уравнении Паули (см. (A.1), (A.2)), которое мы представим в форме
σ0 (cpˆ0 |
− eA0) − 2m hσ pˆ |
− cAi |
|
Ψ(t, r) = 0 , |
|
|
1 |
|
e |
2 |
|
ãäå σ0 единичная матрица. Естественное релятивистское обобщение уравнения Паули выглядит так:
γ0 |
pˆ0 |
− cA0 |
− γ pˆ − cA − m2c2 |
Ψ(x) = 0, |
(C.1) |
||||
h |
|
|
e |
|
e |
i |
2 |
|
|
ãäå γµ = (γ0, γ) некоторые матрицы, а x = (ct, r) 4-радиус-вектор. Представим оператор второго порядка {. . .} в левой части уравнения (1) в факторизованном виде
e |
|
e |
|||
{. . .} = hγµ i~∂µ − |
|
Aµ |
+ mci hγµ i~∂µ − |
|
Aµ − mci . |
c |
c |
||||
Функция Ψ(x) удовлетворяет уравнению (1), если она является решением уравнения
первого порядка |
e |
|
|
|
|
|
hγµ i~∂µ − cAµ − mci Ψ(x) = 0 . |
(C.2) |
Это и есть уравнение Дирака (1928 г.). Конечно, все предыдущее не вывод, а лишь наводящие соображения. Мы постулируем уравнение Дирака в виде (2), а справедливость его подтверждается соответствием следствий из него эксперименту.
Отметим сразу же основное свойство матриц γµ. Решение уравнения Дирака для свободной частицы
(γµpˆµ − mc) Ψ(x) = 0 |
(C.3) |
удовлетворяет также уравнению (1) (при Aµ = 0), которое мы перепишем в форме |
|
(γµpˆµ + mc) (γνpˆν − mc) Ψ(x) = 0 . |
(C.1a) |
Чтобы сохранить обычную связь между энергией и импульсом, E2 = (p2 + m2c2)c2, естественно потребовать, чтобы уравнение (1a) совпадало с уравнением Клейна Фока Гордона (ˆpµpˆµ − m2c2) Ψ(x) = 0. Отсюда следует, что
γµγν + γνγµ = 2gµνI . |
(C.4) |
65
Сколько компонент у волновой функции Ψ(x)? При выяснении этого вопроса важную роль играет инвариантность уравнения Дирака относительно отражений пространственных осей или P -инвариантность.
При повороте на угол ω вокруг оси n преобразование 2-компонентного спинора ϕ имеет вид (A.3)
|
ϕ0 |
= exp |
i |
ωσn |
ϕ = [ cos(ω/2) + i σn sin(ω/2) ] ϕ . |
|
(C.5a) |
|||||||||
|
2 |
|||||||||||||||
Оператор поворота |
|
i |
|
|
|
|
|
-инвариантность, так как и спин (соб- |
||||||||
ственный момент |
|
|
|
|
не нарушает |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ˆs = σ/2, и ось поворота n аксиальные векто- |
||||||||||
|
|
exp |
2 |
ωσn |
|
|
P |
|
|
|
|
|
|
|
||
|
импульса электрона) |
|
|
|
|
|
|
|
|
|||||||
ры, а потому произведение σn истинный скаляр. |
|
|
|
|||||||||||||
Преобразование Лоренца вдоль оси x со скоростью V имеет вид |
|
|
|
|||||||||||||
x0 = x ch ω − ct sh ω , ct0 |
|
|
|
|
|
|
|
1 |
|
|
(V/c) |
|||||
= ct ch ω − x sh ω , ch ω = |
|
|
, sh ω = |
|
|
|
||||||||||
p |
|
p |
|
|||||||||||||
1 − (V/c)2 |
1 − (V/c)2 |
|||||||||||||||
и соответствует гиперболическому повороту в плоскости x, ct, а соответствующее преобразование спинора может быть получено заменой ω → iω в уравнении (5a), ÷òî äà¼ò
ϕ0 = exp −12 ωσx ϕ ,
где быстрота ω определяется соотношением th ω = V/c. В случае преобразования Лоренца, задаваемого произвольным вектором скорости V, имеем
ϕ0 |
|
1 ωσ |
ϕ = [ ch (ω/2) |
|
σn sh (ω/2) ] ϕ , n = |
V |
, th ω = |
V |
. |
(C.6) |
|||
|
|
|
|
||||||||||
|
= exp |
−2 |
n |
нарушает |
|
− |
|
V |
c |
|
|||
Оператор exp |
−21 ωσn |
|
|
P -инвариантность, так как скорость V = V n ïî- |
|||||||||
лярный |
вектор, и следовательно |
σn псевдоскаляр, изменяющий знак при отражении |
|||||||||||
|
|
|
|
||||||||||
координат.
Поэтому для сохранения P -инвариантности уравнения Дирака приходится вводить второй спинор χ с другим, чем у ϕ поведением при отражении координат. Если
ˆ |
ˆ |
(C.7a) |
P ϕ(t, r) = ηP ϕ(t, −r) , P χ(t, r) = −ηP χ(t, −r) , |
||
ãäå ηP фазовый множитель, то преобразование вида
ϕ0 = ϕ ch (ω/2) − σn χ sh (ω/2) , χ0 = χ ch (ω/2) − σn ϕ sh (ω/2) (C.8a)
сохраняет P -инвариантность. Двухкомпонентные спиноры ϕ è χ объединяются в 4- компонентный спинор, или биспинор
Ψ(x) = |
ϕ(x) |
, |
|
χ(x) |
|||
|
|
для которого преобразование (5a), соответсвующее повороту, имеет вид
Ψ0 |
= exp |
i |
ωΣn Ψ = [ cos(ω/2) + i Σn sin(ω/2) ] Ψ , |
(C.5b) |
2 |
||||
а формула (8a), соответствующая преобразованию Лоренца, имеет вид |
|
|||
Ψ0 |
= exp −21 ωαn Ψ = [ ch(ω/2) − αn sh(ω/2) ] Ψ , |
(C.8b) |
||

66 где матрицы
Σ = |
0 σ |
, α = |
σ 0 |
(C.9) |
|
σ 0 |
|
0 σ |
|
являются эрмитовыми и удовлетворяют соотношениям
ΣjΣk = I δjk + iεjkn Σn , αjαk + αkαj = 2I δjk .
Преобразование (7a), соответствующее отражению пространственных координат, может быть записано в виде
ΨP (x) ≡ Pˆ Ψ(t, r) = ηP UP Ψ(t, −r) , UP = UP−1 = |
0 −I . |
(C.7b) |
|
I 0 |
|
Íàéä¼ì 4 × 4 матрицы γµ, рассматривая для простоты уравнение Дирака для свободной частицы (3). При отражении координат оператор pˆ0 не изменяется, а оператор pˆ изменяет знак. Если в уравнении Дирака (γ0pˆ0 − γpˆ − mc) Ψ(t, r) = 0 провести замены
pˆ → −pˆ, Ψ(t, r) → Ψ(t, −r) = ηP−1UP ΨP (x), соответствующие P -отражению, то получим уравнение
(γ0pˆ0 + γpˆ − mc) UP ΨP (x) = 0 .
Таким образом, чтобы функция ΨP (x) удовлетворяла тому же уравнению, что и функ- öèÿ Ψ(x), матрицы γµ должны удовлетворять условиям
UP γ0 = γ0UP , UP γ = −γUP .
Ясно поэтому, что можно выбрать
I 0
γ0 = UP = − .
0 I
Èç UP γ + γUP = 0 следует, что
γ = 0 B ,
C0
а соотношение
γmγn + γnγm = −2δmn I ; m, n = x, y, z
удовлетворяется, если выбрать Bn = −Cn = σn, ãäå σn матрицы Паули. Итак7,
γ0 |
= |
|
0 |
−I |
, |
γ = |
−0σ 0 |
. |
(C.10) |
|
|
|
I |
0 |
|
|
σ |
|
|
C.2. Релятивистская ковариантность уравнения Дирака
Пусть при произвольном преобразовании Лоренца 4-радиус вектор xµ преобразуется по
закону
x0µ = Λµν xν ,
7Наш выбор соответствует так называемому стандартному представлению . Возможны и другие выборы матриц Дирака, получаемые из стандартного при преобразовании γµ → UγµU−1, ãäå U
унитарная матрица.
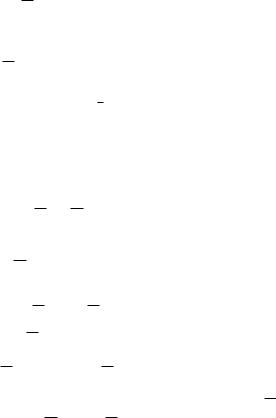
67
а соответсвующее преобразование биспинора Дирака зада¼тся матрицей U:
Ψ0(x0) = U Ψ(x) .
Чтобы доказать релятивистскую ковариантность уравнения Дирака, достаточно пока- зать, что найденные выше операторы γµ преобразуются как 4-векторы, то есть преобразованный оператор U−1γµU удовлетворяет соотношению (ср. с обсуждением преоб-
разования оператора σ относительно поворотов в A.3)
|
|
U−1γµU = Λµν γν . |
|
|
|
|
|
|
|
(C.11) |
||
Это легко проверить непосредственно для поворотов, когда U = exp |
|
i |
ωΣn |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, è äëÿ |
простого преобразования Лоренца, когда U = exp |
21 ωα n |
|
|
|
|
|||||||
|
|
|
|
− |
|
|
. Ïðè ýòîì2 оказываются |
|||||
полезными соотношения |
|
|
|
|
|
|
|
|
|
|||
|
Σ γ0 = γ0 Σ , |
α γ0 = −γ0 α = −γ , |
|
|
|
|
|
(C.12) |
||||
−γkΣj |
ïðè |
j = k , |
|
|
−γ0 |
ïðè |
j = k . |
|
||||
Σjγk = |
−γkΣj = iεjklγl |
ïðè |
j 6= k |
αjγk |
= |
γkαj |
ïðè |
j |
6= k |
|
||
Значит, уравнение (11) справедливо и для общего случая, который всегда можно рассматривать как комбинацию этих двух простых преобразований.
Назовем функцию
Ψ(x) ≡ Ψ+(x)γ0
дираковски сопряженной функции Ψ(x). Она преобразуется по закону
Ψ0(x0) = Ψ+(x) U+γ0 ,
причем, для поворотов (5b), когда U = exp 2i ωΣn , и для простого преобразования Лоренца (8b), когда U = exp −12 ωαn , из (12) следует, что
U+γ0 = γ0U−1 .
Значит, и в общем случае дираковски сопряженная функция преобразуется по закону
Ψ0 = Ψ U−1 ,
откуда видно, что величина
Ψ Ψ = ϕ+ϕ − χ+χ
преобразуется по закону
Ψ0 Ψ0 = Ψ Ψ ,
т. е. является скаляром, а величина Ψ γµΨ преобразуется по закону
Ψ0 γµ Ψ0 = Λµν Ψ γν Ψ ,
т. е. является 4-вектором. Аналогично, можно показать, что величины Ψ γµγνΨ является 4-тензором второго ранга, а величины Ψ γ5Ψ è Ψ γ5γµΨ, ãäå
|
− |
|
|
−I |
0 |
|
|
γ5 = |
|
iγ0 |
γxγyγz = |
0 |
−I |
, |
(C.10a) |
преобразуются как псевдоскаляр и аксиальный 4-вектор соответственно.

68
C.3. Плотность тока
Дираковски сопряженная функция удовлетворяет уравнению
e |
|
−i~∂µ − cAµ Ψ(x) γµ − mc Ψ(x) = 0 . |
(C.13) |
Домножим это уравнение справа на Ψ(x) и вычтем из уравнения (2), домноженного
слева на Ψ(x), тогда получим уравнение
∂µ Ψ(x) γµ Ψ(x) + Ψ(x) γµ ∂µ Ψ(x) = 0 ,
которое можно переписать в виде закона сохранения 4-мерного тока. Если ввести 4- мерную плотность тока
jµ(x) = c Ψ(x) γµ Ψ(x) , |
(C.14) |
то она будет удовлетворять уравнению непрерывности
∂µjµ(x) = 0 .
Для дираковской частицы плотность вероятности
%(x) = j0(x)/c = |
|
|
|
Ψ(x)γ0Ψ(x) = Ψ+(x)Ψ(x) |
(C.15) |
||
является положительно определенной функцией. Плотность 3-мерного тока равна
j(x) = c |
|
|
|
Ψ(x) γΨ(x) = c Ψ+(x)αΨ(x) , |
(C.16) |
||
где эрмитовы матрицы α = γ0γ определены в (9). Уравнение Дирака и плотность дира-
ковского тока, разумеется, инвариантны относительно калибровочного преобразования (4.8).
C.4. Зарядовое сопряжение и отражение времени
Рассмотрим еще свойство уравнения Дирака относительно C (зарядовое сопряжение) преобразования. Если функция Ψ(x) удовлетворяет уравнению (2), то легко проверить, что функция
ΨC (x) = C |
|
|
|
Ψ(x) , C = γyγ0 = −αy |
(C.17) |
||
соответствует зарядово-сопряженной частице, т. е. удовлетворяет уравнению
e |
|
hγµ i~∂µ + cAµ − mci ΨC (x) = 0 , |
(C.2b) |
которое отличается от уравнения (2) для Ψ(x) лишь знаком заряда e.
Аналогично, если функция Ψ(x) удовлетворяет уравнению (3), то легко проверить, что функция
ΨT (t, r) = UT |
|
|
|
Ψ(−t, r) , UT = iγzγxγ0 |
(C.18) |
||
удовлетворяет тому же уравнению. Наконец, укажем, что действие тр¼х преобразований C, P è T определяется соотношением:
− |
− |
|
|
− |
|
−I |
0 |
|
|
ΨCP T (t, r) = iγ5Ψ( t, |
|
r) , γ5 |
= |
iγ0 |
γxγyγz = |
0 |
−I |
. |
(C.19) |

69
C.5. Гамильтонова форма уравнения Дирака
Умножив уравнение (2) на γ0 слева, получим уравнение Дирака в гамильтоновой форме
i~ |
∂Ψ |
ˆ |
ˆ |
2 |
|
+ eA0 , pˆ = −i~r . |
|
|
∂t |
|
= H Ψ, |
H = α(cpˆ |
− eA) + mc |
γ0 |
(C.20) |
||
Отсюда оператор скорости равен
|
|
|
|
|
|
|
vˆ = |
i |
ˆ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
~ |
[H, r] = c α , |
|||||||||||
а операторное уравнение движения во внешнем поле |
|||||||||||||||||||
|
|
d |
|
|
|
e |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
pˆ − |
|
A = eE + eα × B |
|||||||||||
|
dt |
c |
|||||||||||||||||
является аналогом классического уравнения движения |
|||||||||||||||||||
|
d |
|
mv |
|
|
|
|
v |
|||||||||||
|
|
|
|
|
|
|
|
|
= eE + e |
|
× B . |
||||||||
dt |
|
|
|
|
|
c |
|||||||||||||
|
1 (v/c)2 |
||||||||||||||||||
В центральном поле (при Ap=−0, eA0 = U(r)) орбитальный момент |
|||||||||||||||||||
ñïèí |
|
|
|
|
|
ˆs = 2 Σ = |
2 |
0 σ |
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
σ 0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(C.21)
ˆl = r × pˆ/~ è
в отдельности не сохраняются:
ˆ |
|
i |
|
|
c |
|
|
dl |
|
|
ˆ ˆ |
α × pˆ, |
|||
dt |
= |
~ |
[H, l] = |
~ |
|||
dˆs |
|
|
i |
ˆ |
c |
|
|
dt |
= |
~ |
[H, ˆs] = − |
~ |
α × pˆ . |
||
ˆ ˆ ˆ
j = l + s,
ˆ
dj i ˆ ˆ
dt = ~[H, j] = 0 .
Рассмотрим теперь свободный электрон в состоянии с определенным импульсом p. В этом случае гамильтониан
ˆ |
2 |
γ0 |
H = cαp + mc |
||
также, вообще говоря, не коммутирует с оператором спина,
ˆ |
(C.22) |
[H, ˆs] = i c α × p . |
Однако последняя формула подсказывает два возможных исключения.
1. Åñëè p → 0 (что справедливо в системе покоя электрона), то правая часть уравнения (22) обращается в нуль
ˆ |
(C.23) |
[H, ˆs] = 0 ïðè p → 0 . |
Таким образом, спиновое состояние свободного электрона можно описывать, задавая определенное значение σ = ±1/2 оператора sˆz в системе покоя электрона.
2. Если умножить уравнение (22) скалярно на вектор p, то правая часть полученного
соотношения также обратится в нуль. Поэтому оператор спиральности ˆ Λ (проекции
спина на направление импульса электрона) коммутирует с гамильтонианом
ˆ |
ˆ |
ˆ |
· |
p |
|
|
[H, Λ] = 0 , |
Λ = ˆs |
|p| |
. |
(C.24) |
||
Собственные значения оператора |
ˆ |
|
|
|
|
|
|
Λ равны λ = ±1/2, а его собственные состояния на- |
|||||
зываются спиральными состояниями.
70
D. Свободное движение дираковской частицы
Cвободному движению частицы с определ¼нным 4-импульсом p соответствует плоская волна8
Ψ(x) = u(p) e−ipx , p x ≡ pµxµ = Et − pr , |
(D.1) |
где биспинор u(p) удовлетворяет системе алгебраических уравнений |
|
(γµpµ − m) u(p) = 0 . |
(D.2) |
Для двухкомпонентных спиноров ϕ(p) è χ(p), через которые выражается биспинор
ϕ(p) u(p) = u(E, p) = ,
χ(p)
получаем систему уравнений
(E − m) ϕ − σp χ = 0 , σp ϕ − (E + m) χ = 0 .
Эта система имеет ненулевое решение, если ее определитель равен нулю, то есть если E2 = p2 + m2. Введ¼м арифметический, положительный корень
p
ε = + p2 + m2 . (D.3)
Существуют две возможности: 1. Энергия положительна:
E = +ε , χ = |
σp |
ϕ . |
|
ε + m |
|||
|
|
При нормировке
ϕ+ϕ = 1 , uu¯ = 2m
получаем биспинор
u(ε, p) ≡ up = |
|
|
|
, Aˆ = √ε + m = √ε − m σn , |
(D.4a) |
|||||
|
Aˆ ϕ |
|||||||||
|
√ε + mϕ |
|
|
σp |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ãäå n = p/|p|, ïðè ýòîì
u¯p up = 2m , u¯p γµ up = 2pµ . |
(D.4b) |
|||||
2. Энергия отрицательна: |
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
E = |
− |
ε, u( ε, p) = |
−A χ |
. |
||
|
− |
√ε + m χ |
|
|||
Четыре компоненты волновой функции соответствуют двум возможным ориентациям спина при двух возможных знаках энергии. Исключить состояния с отрицательной энергией нельзя, так как в квантовой механике возможны переходы между состояниями. Дирак постулировал, что уровни с отрицательной энергией заполнены. Тогда переходов на них нет в силу принципа Паули. Дырка в дираковском море ведет себя как
8Здесь и ниже (за исключением F.1) полагаем ~ = 1, c = 1.
