Лекция 7, 8. Аксиоматика Гильберта трехмерного евклидова пространства. Первая и вторая группы аксиом Гильберта и основные следствия из них.
Литература [1] § 71, 72, [2] § 10 ‑ 11.
Основные объекты представляют собой элементы трех множеств: множества точек, прямых и плоскостей. Еще раз следует подчеркнуть, что природа основных объектов не имеет никакого значения при построении аксиоматической теории. Для построения геометрии евклидова пространства абсолютно не существенно, что мы будем понимать под точками, прямыми и плоскостями, необходимо, чтобы они вместе с основными отношениями удовлетворяли требованиям аксиом. Структура системы аксиом Гильберта довольно сложна, она традиционно подразделяется на пять групп:
-
Первая группа аксиом, аксиомы принадлежности – 8 аксиом.
-
Вторая группа аксиом, аксиомы порядка – 4 аксиомы.
-
Третья группа аксиом, аксиомы конгруэнтности – 5 аксиом.
-
Четвертая группа аксиом, аксиомы непрерывности – 2 аксиомы.
-
Пятая группа аксиом, аксиомы параллельности – 1 аксиома.
Аксиомы принадлежности.
Обозначим множество точек через М,
множество прямых через L,
а множество плоскостей через P.
На декартовых произведениях
 и
и
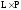 введем бинарные отношения
введем бинарные отношения
 и
и
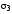 ,
которые будем называть отношениями
принадлежности. Если точка А и прямая
l находятся в отношении
,
которые будем называть отношениями
принадлежности. Если точка А и прямая
l находятся в отношении
 ,
т.е. пара (А, l)
,
т.е. пара (А, l)
 ,
то будем говорить, что точка А принадлежит
или лежит на прямой l, или,
что то же самое, прямая l
проходит через точку А или ее содержит.
Аналогично, если А – точка, а
- плоскость и
,
то будем говорить, что точка А принадлежит
или лежит на прямой l, или,
что то же самое, прямая l
проходит через точку А или ее содержит.
Аналогично, если А – точка, а
- плоскость и
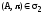 ,
то будем использовать следующую
терминологию: точка принадлежит
плоскости, точка лежит на плоскости,
плоскость содержит точку или плоскости
проходит через эту точку. В случае, когда
прямая l и плоскость
находятся в отношении
,
то будем использовать следующую
терминологию: точка принадлежит
плоскости, точка лежит на плоскости,
плоскость содержит точку или плоскости
проходит через эту точку. В случае, когда
прямая l и плоскость
находятся в отношении
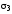 ,
т.е.
,
т.е.
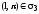 ,
то будем говорить: прямая лежит,
принадлежит или содержится в плоскости,
а плоскость содержит или проходит через
эту прямую. Точки, прямые и плоскости
должны удовлетворять следующим аксиомам.
,
то будем говорить: прямая лежит,
принадлежит или содержится в плоскости,
а плоскость содержит или проходит через
эту прямую. Точки, прямые и плоскости
должны удовлетворять следующим аксиомам.
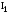 .
Каковы бы ни были две точки А и В,
существует прямая а, проходящая через
эти две точки.
.
Каковы бы ни были две точки А и В,
существует прямая а, проходящая через
эти две точки.
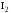 .
Каковы бы ни были две точки А и В,
существует не более одной прямой а,
проходящей через эти две точки.
.
Каковы бы ни были две точки А и В,
существует не более одной прямой а,
проходящей через эти две точки.
 .
На каждой прямой лежит, по крайней мере,
две точки. Существует, по крайней мере,
три точки, не принадлежащие одной прямой.
.
На каждой прямой лежит, по крайней мере,
две точки. Существует, по крайней мере,
три точки, не принадлежащие одной прямой.
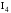 .
Каковы бы ни были три точки А.В и С, не
лежащие на одной прямой, существует
плоскость , проходящая
через эти три точки. На каждой плоскости
лежит, по крайней мере, одна точка.
.
Каковы бы ни были три точки А.В и С, не
лежащие на одной прямой, существует
плоскость , проходящая
через эти три точки. На каждой плоскости
лежит, по крайней мере, одна точка.
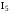 .
Каковы бы ни были три точки, не лежащие
на одной прямой, существует не более
одной плоскости, содержащей эти точки.
.
Каковы бы ни были три точки, не лежащие
на одной прямой, существует не более
одной плоскости, содержащей эти точки.
 .
Если две точки А и В прямой а лежат в
плоскости , то любая
точка, принадлежащая прямой а, принадлежит
плоскости .
.
Если две точки А и В прямой а лежат в
плоскости , то любая
точка, принадлежащая прямой а, принадлежит
плоскости .
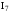 .
Если две плоскости
и имеют общую точку
А, то существует, по крайней мере, еще
одна В, принадлежащая этим плоскостям.
.
Если две плоскости
и имеют общую точку
А, то существует, по крайней мере, еще
одна В, принадлежащая этим плоскостям.
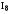 .
Существует, по крайней мере, четыре
точки, не лежащие в одной плоскости.
.
Существует, по крайней мере, четыре
точки, не лежащие в одной плоскости.
10. Две прямые имеют не более одной точки.
20. Если две плоскости имеют общую точку, то они имеют общую прямую.
30. Через прямую и не лежащую на ней точку проходит одна и только одна плоскость.
40. Через две пересекающиеся прямые проходит одна и только одна плоскость.
50. На каждой плоскости существует три точки, не лежащие на одной прямой.
Заметим, что из аксиом первой группы
не следует, что множество основных
элементов, точек, прямых и плоскостей,
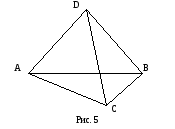
бесконечно. Рассмотрим модель, доказывающую
это утверждение. Пусть дано множество,
состоящее из четырех элементов: A,
B, С и D. Для
наглядности расположим их в вершинах
тетраэдра (рис. 5). Под точками будем
понимать элементы A, B,
С и D (вершины тетраэдра),
под прямыми – неупорядоченные пары
элементов AB, AC,
AD, BC, BD
и CD (ребра тетраэдра), а
под плоскостями - неупорядоченные тройки
этих элементов ABC, ABD,
ACD и BCD (грани
тетраэдра). Точка принадлежит прямой
или плоскости, если она входит в
соответствующую пару или тройку точек,
а прямая принадлежит плоскости, если
она как пара точек входит в тройку точек,
определяющую плоскость. Выполнение
требований аксиом
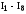 проверяется достаточно просто. Например,
рассмотрим требование аксиомы
проверяется достаточно просто. Например,
рассмотрим требование аксиомы
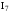 .
Очевидно, оно выполняется, так как в
тетраэдре если две грани имеют общую
вершину, то они пересекаются по ребру,
т.е. имеют еще одну общую вершину.
Выполнение остальных аксиом проверьте
самостоятельно.
.
Очевидно, оно выполняется, так как в
тетраэдре если две грани имеют общую
вершину, то они пересекаются по ребру,
т.е. имеют еще одну общую вершину.
Выполнение остальных аксиом проверьте
самостоятельно.