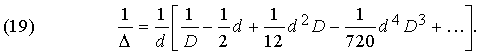Практика 2

ϑ

872

1045

1219

1392

1564

1736

1908

2079

2250

2419

2588

2756

2924

3090

3256

3420

3584

3746

3907

467

4226

4384

4540

4695

Δ

10

12

11

16

19

22,5

24

27

29,5

31,3

33,9

37,8

39,9

43

47

49,9

52,7

55,3

57,9

59,8

63

66

68

71,3

ϭ

1,1%

1,14%

0,9%

1,14%

1,2%

1.18%

1,25%

1,28%

1,31%

1,33%

1,34%

1,36

1,39

1,5

1,52

1,59

1,593

1,61

1,62

1,64

1,666

1,711

1,712

1,73

ϑ

4848

0500

5150

5299

5446

5592

5736

5878

6018

6157

6293

6428

6561

6691

6820

6947

7071

7193

7314

7431

7547

7660

7771

7880

Δ

73,6

75,7

79,8

83

87

84

86

88,7

90,23

97.3

102

107

112

117

122

127

132,4

139,1

145,3

149

ϭ

1,51

1,518

1,52

1,56

1,58

1.6

1.63

1.66

1.69

1.73

1.63

1.64

1,7

1,74

1,78

1,82

1,86

1,89

1,9

1,93

ϑ

7986

8090

8192

8290

8387

8480

8572

8660

8746

8829

8910

8988

9063

9135

9205

9272

9336

9397

9455

9511

9563

9613

9659

9703

Δ

ϭ

КОНЕЧНЫЕ РАЗНОСТИ. Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой-нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово «конечные» используется здесь в несколько устаревшем смысле «не бесконечно малые», т.е. не связанные с предельными переходами. Поскольку дифференциальное исчисление занимается изучением пределов разностей, а исчисление конечных разностей – самими разностями, то естественно, что между этими двумя теориями существуют много параллелей. Исчисления конечных разностей используются при интерполяции в математических таблицах, при суммировании числовых рядов, при вычислении интегралов и дифференцировании функций. Разности встречаются также в любой ситуации, когда надо описать поведение объекта, который испытывает воздействие меняющихся условий на определенном расстоянии (во времени и в пространстве). Например, термостату требуется значительное время, чтобы отреагировать на изменение температуры, поэтому он реагирует не на текущую температуру, а на ту, что была минуту назад. Другой пример: автомашиной управляет водитель, которому требуется какое-то время, чтобы отреагировать на возникшую на дороге ситуацию.

Под конечной разностью первого порядка функции f (x) принято понимать величину

где d – некоторая постоянная, которую часто, но не всегда, принимают равной 1. Разность второго порядка обозначается ²f и представляет собой разность разностей, т.е.

Продолжив этот процесс, мы получим разности более высоких порядков ³f (x), ⁴f (x), .

Данные выше определения можно также применить к членам любых последовательностей величин, например, к последовательности

3, 6, 11, 18, 27, 38, 

Первые разности равны

6 – 3, 11 – 6, 18 – 11, 27 – 18, 38 – 27, ,

т.е.

3, 5, 7, 9, 11, ;

разности второго порядка постоянны и равны 2.

В общем виде такие последовательности можно записать как

где разности первого, второго и т.д. порядков определяются выражениями

а n может принимать любое допустимое для индекса значение.

В некоторых приложениях используются последовательности вида

где индексы могут принимать любые убывающие значения. В этом случае вместо символа используется символ «разделенной разности». Разделенные разности первого и второго порядков определяются следующим образом:

Помимо уже названных выше приложений, исчисление конечных разностей используется в страховании, теории вероятностей и статистике. В последние годы с изобретением быстродействующих компьютеров конечные разности стали все более широко применяться при решении дифференциальных уравнений, обыкновенных и в частных производных, многие из которых ранее было невозможно решить другими математическими методами.

У истоков теории. Хотя исследование свойств и использование конечных разностей приходится на современный период развития математики, Птолемей (ок. 150 н.э.) ввел в Альмагесте таблицу разностей первого порядка, чтобы облегчить расчеты в таблице длин хорд. Разности второго порядка использовал при вычислении своих таблиц логарифмов в 1624 Г.Бриггс. Теория интерполяции берет начало со знаменитой пятой леммы из 3-й книги Математических начал (1687) И.Ньютона, в которой впервые была приведена формула, носящая ныне его имя. Частный случай формулы Ньютона, открытый также независимо его современником Дж.Грегори (1638–1675), приведен ниже (см. формулу (7)). В общей формуле интерполяции Ньютона использовались разделенные разности, хотя этот термин, по-видимому, был введен О.де Морганом (1806–1871) в 1848. Первое применение исчисления конечных разностей к задачам теории вероятностей принято связывать с именами П.де Монтмора (1678–1719) и А.де Муавра (1667–1754).

Хотя Л.Эйлер (1707–1783) в своих работах по дифференциальному исчислению использовал предельные переходы в конечных разностях, основания современной теории конечных разностей были заложены в основном Ж.Лагранжем (1736–1813) и П.Лапласом (1749–1827). Первый из них ввел в исчисление конечных разностей символические методы, второй сделал конечные разности главным инструментом в своей Аналитической теории вероятностей (1812).

Под влиянием этих работ математики 19 в. принялись интенсивно разрабатывать предмет, и в 1860 Дж.Буль выпустил свой классический Трактат об исчислении конечных разностей. С тех пор это исчисление и круг его приложений существенно расширились. Одно из наиболее важных приложений конечные разности нашли в статистике. Особенно полезными они оказались в теории сериальной корреляции, в анализе случайных последовательностей и статистических временных рядов.

Интерполяция. Чтобы понять, как конечные разности используются при интерполяции, рассмотрим следующую таблицу:

Величины в первом столбце таблицы называются значениями аргумента, во втором – табличными значениями функции. В трех следующих столбцах приведены разности первого, второго и третьего порядков. Числа 7, 12, 6 называются «ведущими» или «диагональными разностями», соответствующими первому аргументу. Термин «диагональные» использован потому, что разности относительно соответствующих аргументов и табличных значений располагаются не по горизонтали.

Величина (¹/₂) (19 + 37) = 28 называется центральной разностью, соответствующей третьему аргументу, и обозначается символом . Греческая буква  означает среднее,  – среднее соседних разностей. Величина 18 называется центральной разностью второго порядка и обозначается символом² . Термин «центральная» указывает на то, что эти разности расположены по центру относительно аргумента, т.к. они либо лежат на одной горизонтали с аргументом, либо являются средними значений, расположенных по соседству с этой горизонталью.

Обобщая, таблицу величин можно записать в символических обозначениях следующим образом:

Величины  f (x), ² f (x), ³ f (x) представляют собой диагональные разности, соответствующие аргументу x. Если мы захотим найти табличные значения для аргумента x + pd, где p – некоторое произвольно выбранное число, то необходимо подставить соответствующие значения в следующий ряд, известный под названием интерполяционной формулы Грегори – Ньютона (в русскоязычной литературе эту формулу принято называть формулой Ньютона):

где 2! (читается «два факториал») означает 12, 3! = 12 3 и т.д.

В литературе встречается несколько вариантов формулы Грегори – Ньютона. В некоторых из них вместо диагональных разностей используются центральные разности. Так, центральные разности, соответствующие аргументу x, определяются следующим образом:

и т.д.

В качестве примера найдем по формуле интерполяции значение (2,5)³ из приведенной выше числовой таблицы. Так как d = 1, p = ¹/₂ и диагональные разности, соответствующие x = 2, равны  = 19, ² = 18,³ = 6, находим по формуле интерполяции

Символические методы. Один из наиболее удивительных аспектов исчисления конечных разностей связан с символическими (или операторными) методами. Чтобы понять их суть, рассмотрим символ E,называемый оператором и определяемый соотношением

Пусть E ²f (x) – результат действия E на Ef (x), тогда E ²f (x) = f (x + 2d). Пользуясь математической индукцией, получаем для произвольного индекса p формулу

Опустим в формуле (8) символ функции и рассмотрим соотношение между одними лишь символами E= 1 + . Оказалось, что с этим равенством и с другими, выводимыми из него, можно обращаться в соответствии с обычными правилами алгебры. Если степени символов интерпретировать как результат последовательного применения операторов Е и , то полученные формулы также будут справедливы. Рассмотрим, например, E^p = (1 + )p. Если правую часть равенства разложить по формуле бинома, а полученный ряд применить к f (x), мы получим разложение, стоящее в правой части интерполяционной формулы (7).

Из (9) следует, что запись E^pf (x) эквивалентна f (x + pd). Таким образом, биномиальное разложение, примененное к f (x) как операторное и приравненное к f (x + pd), дает формулу Грегори – Ньютона.

Этот пример иллюстрирует характерные особенности символического (операторного) метода. Он позволил открыть так много замечательных формул, что большинство авторов, впервые его применивших, в своих работах не могли не выразить своего восхищения его мощью. Тайна эффективности этого метода кроется в том, что основной закон комбинирования алгебраических величин, с одной стороны, и операторы, такие, как  и Е, с другой, удовлетворяют правилу сложения показателей степеней

Следует иметь в виду, однако, что в первом случае символ произведения интерпретируется как обычное умножение, а во втором как последовательное выполнение операций.

Символические методы позволяют установить связь исчисления конечных разностей с дифференциальным исчислением. Чтобы убедиться в этом, обозначим производную от f (x) символомDf (x), вторую производную – символом D ²f (x) и т.д. Разложение f (x + d) в ряд Тейлора (см. МАТЕМАТИЧЕСКИЙ АНАЛИЗ) можно записать символически в виде

Учитывая, что разложение в ряд функции e^z, где e = 2,71828 – основание натуральных логарифмов, имеет вид

разложение (10) можно записать как

Опуская, как и прежде, символ функции, получаем чисто символическое уравнение

Если разрешить его относительно D по обычным правилам алгебры и принять во внимание разложение в ряд Тейлора для логарифмической функции, то получим

т.е.

Еще более замечательные соотношения получаются для обратных операторов D^–1 и ^–1. Первый оператор интерпретируется как символ интегрирования , а второй – как символ суммирования , определяемый следующим образом:

Хотя D^–1 и ^–1 следует рассматривать как символы операторов, примечательно, что над ними можно производить алгебраические операции так, как если бы это были величины ¹/_D и ¹/_.

В качестве примера применения символического метода решим уравнение (13) относительно ¹/_:

Для интерпретации этого соотношения необходимо иметь в виду разложение

где B₁ = ¹/₆, B₂ = ¹/₃₀, B₃ = ¹/₄₂ – т.н. числа Бернулли, названные так в честь открывшего их Я.Бернулли (1654–1705). Эти числа используются в различных разделах исчисления конечных разностей. Бернулли с гордостью заявлял, что с их помощью он нашел сумму десятых степеней первой тысячи натуральных чисел «за половину четверти часа».

Подставив x вместо dD в правой части разложения (18) и сделав небольшие преобразования, можно записать (17) в виде

Вспомнив, что означали эти символы, и применив формулу к f (x), получим следующее разложение:

Суммирование рядов. Метод конечных разностей особенно удобен при суммировании рядов. Чтобы убедиться в этом, предположим, что в (1) d = 1, и рассмотрим сумму

которую можно записать в более компактном виде

Заметим, что

откуда

Тот же результат можно получить и из формулы (20). В этом случае, полагая d = 1 и f (x) = x, получаем

Разностные уравнения. В некоторых приложениях метода конечных разностей встречаются уравнения, типичными примерами которых являются следующие:

Такие уравнения называются «разностными уравнениями», так как их можно превратить в соотношения между разностями u. Например, первое уравнение можно записать в виде u_x = (x – 1)u_x, а второе – в виде ²u_x + ³/₂ u_x = 0. Первое называется разностным уравнением первого порядка, второе – второго порядка.

Такие уравнения встречаются, в частности, в приложениях теории вероятностей, для нахождения последовательных значений величины u_x, когда x пробегает некоторую последовательность целых чисел. Такие образом, для уравнения (21), если u₁ =1 и x = 2, 3, 4, , n, получаем

Аналогично, для (22), если u₀ = 1, u₁ = 0 и x = 2, 3, 4, , n, мы получаем следующую последовательность значений:

В общем случае разностные уравнения имеют также решения, определяемые в непрерывной области значений x. Например, частным решением уравнения (21) является «гамма-функция»  (x), так как одно из фундаментальных свойств этой функции состоит в том, что  (x + 1) = x (x) (см. ФУНКЦИЯ).

Такое решение мы получим из уравнения (22), положив u_x = m^x. Подставляя эту функцию в (22), мы получаем уравнение

откуда m = 1, m = –¹/₂. Следовательно, уравнение (22) имеет решение

где А и В – произвольные постоянные. В частности, для A = ¹/₃ и B = ²/₃ мы получим при целочисленных значениях x последовательность (23).

Но (24) – не самое общее решение уравнения (22), так как другое решение можно получить, умножив любое частное решение на g (x), где g (x) – произвольная функция единичного периода, т.е. удовлетворяет уравнению

Примерами таких функций могут служить sin2x, cos2x, sin6x, cos6x и т.д.

Подставляя в (22)

нетрудно убедиться в том, что u_x – решение уравнения (22). Это решение получено при умножении второго члена в правой части (24) на подходящим образом выбранную функцию единичного периода.