Шкала отношений (масштабная)

В шкалах отношений могут быть выражены величины, удовлетворяющие (в дополнение к требованиям интервальных шкал) аксиомам аддитивности:

1. Если A = P и B > 0, то (A + B) > P.

2. A + B = B + A.

3. Если A = P и B = Q, то A + B = P + Q.

4. (A + B) + C = A + (B + C).

Здесь инвариантом является отношениевеличин. Так, если x_i иy_i– сутьi‑е измерения одной и той же величины в различных шкалах отношений, тоx₁/x₂=y₁/y₂, т. е. результаты измерения в разных шкалах отношений связаны соотношениемy= ax, (a0).

Это означает, что в шкале отношений есть абсолютныйнуль(начало отсчета) и остается свобода только в выборе единицы измерения.

Примеры: абсолютная температура в шкале Кельвина, длина, вес, масса, электрическое сопротивление, деньги.

Допустимые операции: над отношениями величин можно выполнять любые арифметические и другие операции.

Натуральная (абсолютная шкала)

Здесь есть и абсолютный нуль(начало отсчета), иабсолютная единица. Фактически – это безразмерные арифметические величины. Их можно использовать, кроме всего прочего, в качестве показателя степени и аргумента логарифма.

Примеры: гармонические отношения размеров, звуков; кардинальная арифметика (конечных и бесконечных множеств), законы теории размерности, подобия, топологии (связность) и т.п.

Основной вывод к подразделу 6.3

Выбор шкалы измерения должен ориентироваться на объективные отношения, которым подчиняется наблюдаемая величина. Применение более слабой шкалы правомерно, но расточительно, так как приводит к потерям части полезной информации. Применение же более сильной шкалы может привести к неверным выводам, так как в этом случае осуществляется апелляция к свойствам, которые экспериментально установлены не были.

Типичная ошибка: после оцифровки ранговых или интервальных шкал с числовыми метками начинают обращаться как с обычными (безразмерными) числами. Это характерно для вычисления всевозможных рейтингов, средних баллов и т.п.

12.Учет неопределенностей с помощью вероятностного описания.

Вероятностное описание ситуации

Вероятностное описание применяется для описания ситуаций, включающих случайные события или процессы. Случайность – это вид неопределенности, подчиняющийся строгой закономерности, которая выражается распределением вероятностей. При вероятностном (стохастическом) описании вероятностные характеристики (закон распределения и все его параметры и моменты) являются детерминированными. Случайность изучается в рамках двух дисциплин: теории вероятностей и математической статистики.

Теория вероятностей(ТВ) – по известным (заданным) вероятностным характеристикам элементарных событий (объектов) определяются вероятностные характеристики составленных из них сложных событий (объектов).

Математическая статистика(МС) – по результатам экспериментов (реальных или умозрительных) с составными событиями (объектами) позволяет оценивать вероятностные характеристики элементарных событий (объектов), из которых они составлены.

Важно то, что результаты, полученные и с помощью ТВ, и с помощью МС, справедливы лишь при выполнении допущения о существовании (реальном или умозрительном) вероятностей. Сами вероятности непосредственному измерению не поддаются. Статистические методы дают правильный результат только при условии существования вероятностей. Однако непосредственно проверить это по экспериментальным данным нельзя. МС занимается только проверкой гипотез, но сама гипотезы выдвигать не может. При этом и сам ответ о правомочности той или иной гипотезы также выдается в вероятностном смысле. С учетом этого следует иметь в виду, что сами по себе статистические методы не могут ничего доказать или опровергнуть. Это отражено в известном фольклорном изречении: существует три вида лжи – ложь, несусветная ложь и матстатистика. Важно понимать, что такого рода сомнения относятся к сфере интерпретации статистических результатов, но не к способу их получения.

На практике вероятностные оценки вероятностных характеристик реальных объектов получаются с помощью статистических измерений, основными задачами которых являются:

•  определение (идентификация) закона распределения;

•  определение параметровраспределения известного вида.

В связи с вероятностным подходом полезно различать связи между явлениями двух типов: причинно-следственные и корреляционные.

В случае причинно–следственных(каузальных) связей явление Aс неизбежностью влечет за собой наступление явленияB, что можно отразить схемой A  B.

В случае корреляционнойсвязи два явления взаимообусловлены: оба происходят или оба не происходят, но выявить какое из них является причиной, а какое – следствием обычно не представляется возможным, хотя и не исключается вовсе, т. е. корреляционная связьA  Bестьсимметричноеотношение. Обычно наличие корреляционной связи является следствием существования некоторой общей скрытой причины, что можно отразить диаграммой:

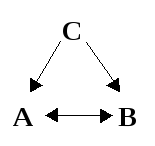
Корреляционную связь всегдаможно количественно оценить по экспериментальным данным путем оценки коэффициента взаимной корреляции. Дляподтвержденияпричинно-следственной связи нужно отыскать истинную причину и следствие, но, к сожалению, общих методов для решения этой задачи нет.

13.Учет неопределенностей на базе теории расплывчатых (нечетких) множеств.

Основоположником теории считается Л. Заде [Error: Reference source not found].

Некоторые типичные вопросы и ситуации, связанные с нечеткостью понятий:

–  из скольких песчинок состоит куча;

–  сколько волосинок должно выпасть, чтобы человек считался лысым;

–  шкала возрастов: младенец– ребенок– подросток– юноша– молодой человек– мужчина– пожилой– старец...

Расплывчатое множество Aзадается двумя атрибутами: A= {(x,_A(x))},

где xX,X– запас элементов (обычное множество),

_A(x) – функция принадлежности.

Функция принадлежности _A(x) характеризует степень принадлежности элемента к множеству: 0_A(x)1. Крайние значения соответствуют обычной функции принадлежности:

_A(x) = 1  xA;

_A(x) = 0  xA.

Во всех остальных случаях значение функции _A(x) задает меру принадлежности.

Носитель S(A) расплывчатого множества A– это подмножество таких элементов xS(A)X, для которых_A(x) > 0.

Основные теоретико-множественные операции могут быть обобщены на случай расплывчатых множеств: A= {(x, _A(x)},B= {(x, _B(x)},C= {(x, _C(x)}_, построенных на одном и том же запасе элементовX.

1. Равенство:A= B _A(x) =_B(x)xX 

2. Включение:A B  _A(x) <_B(x)xX 

3. Пересечение:C=AB _C(x) =min[_A(x), _B(x)]xX 

4. Объединение:C=A  B  _C(x) =max[_A(x), _B(x)]xX 

На базе этих операций строится теория расплывчатых множеств, которая позволяет решать задачи при наличии расплывчатости в исходных данных. Следует подчеркнуть, что смысл и конкретные значения функции принадлежности _A(x) никак не определяются и не интерпретируются внутри самой теории расплывчатых множеств. Это должно определяться из исходной содержательной постановки задачи. При этом результат решения также будет выражен в терминах расплывчатых множеств.

14.Регистрация экспериментальных данных и основные виды их обработки для классификационных и числовых моделей.