diskr_matem

ПРЕДИСЛОВИЕ

Дискретная математика – одна из важнейших составляющих современной математики. В отличие от других математических дисциплин учебного плана направления бакалавриата «Бизнес-информатика», таких как математический анализ, линейная алгебра и др., дискретная математика имеет дело с объектами нечисловой природы, что позволяет, в частности, использовать ее методы для моделирования социальных и экономических процессов. Понятия и методы дискретной математики необходимы для постановки различных прикладных задач, для усвоения и разработки современных информационных технологий, лежат в основе теории и практики программирования.

Целью изучения дисциплины «Дискретная математика» является освоение соответствующего математического аппарата, позволяющего анализировать, моделировать и решать прикладные (в том числе экономические) задачи.

Задачи изучения вытекают из требований к результатам освоения программы бакалавриата компетенций, установленных Федеральным государственным образовательным стандартом высшего профессионального образования (ФГОС-3+) по направлению 38.03.05 «Бизнес-информатика».

Входе изучения дисциплины ставятся задачи:

‒освоение методов дискретной математики для решения прикладных

задач;

‒выработка умения моделировать реальные объекты и процессы с использованием математического аппарата дискретной математики;

‒развитие логического и алгоритмического мышления студентов, повышение уровня их математической культуры;

‒развитие навыков самостоятельной работы по изучению учебной и научной литературы.

Знания, полученные студентами в процессе изучения дисциплины «Дискретная математика», необходимы для изучения дисциплин математического и естественнонаучного цикла («Теория вероятностей и математическая статистика», «Методы оптимальных решений», «Языки и методы программирования»), а также ряда дисциплин профессионального цикла.

Всоответствии с ФГОС-3+ по направлению «Бизнес-информатика». квалификация академический бакалавр, процесс изучения дисциплины «Дискретная математика» на формирование следующих компетенций:

общекультурных компетенций (ОК)

– способность к самоорганизации и самообразованию (ОК-7);

профессиональных компетенций (ПК)

– способность использовать основные методы естественнонаучных дисциплин в профессиональной деятельности для теоретического и экспериментального исследования (ПК-17);

3

–способность использовать соответствующий математический аппарат

иинструментальные средства для обработки, анализа и систематизации информации по теме исследования (ПК-18);

–умение готовить научно-технические отчеты, презентации, научные публикации по результатам выполненных исследований (ПК-19).

Врезультате изучения дисциплины студент должен:

а) знать основные понятия теории множеств, комбинаторики, математической логики, теории графов и теории алгоритмов, используемых в экономических исследованиях при разработке новых информационных технологий и при изучении других дисциплин математического и естественнонаучного, профессионального циклов;

б) уметь:

–применять методы дискретной математики для решения прикладных

задач;

–строить математические модели прикладных задач.

в) владеть навыками решения задач дискретной математики.

По дисциплине ««Дискретная математика» студенты бакалавриата направления «Бизнес-информатика» должны выполнить одну контрольную работу (задания к которым приводятся в данном пособии). Контрольная работа (в соответствии с учебным графиком) могут быть существенно дополнена за счет частичного использования компьютерной обучающей программы (КОПР). В процессе изучения дисциплины студенты проходят компьютерное тестирование и сдают экзамен.

При выставлении итоговой оценки студента по данной дисциплине учитываются балльная оценка текущей успеваемости (качество подготовки и работа на практических занятиях, выполнение контрольной работы, компьютерное тестирование, посещение занятий) и результаты сдачи экзамена.

.

Содержание дисциплины и

4

методические рекомендации по ее изучению

Ниже по каждой теме приводится учебно-программный материал1, который должен изучить студент со ссылками на рекомендованные учебники и учебные пособия.

Контрольные вопросы по каждой теме представлены ниже в разделе «Вопросы для самопроверки».

Рекомендуемые по каждой теме задачи с решениями и для самостоятельной работы приводятся ниже в разделе «Задачи для самоподготовки».

Вопросы выполнения контрольных работ с частичным использованием КОПР рассматриваются в брошюре [Электронные ресурсы, 3]: «Математика. Методические указания по проведению и выполнению контрольных работ с использованием КОПР».

Тема 1. Множества, функции, отношения

Множества – основные понятия. Диаграммы Венна. Операции над множествами: объединение, пересечение, дополнение. Кортежи и прямое (декартово) произведение множеств. Соответствия и их свойства. Взаимно однозначные соответствия. Мощности бесконечных множеств. Принципы включений – выключений. Понятие функции. Обратные функции. Суперпозиции и формулы. Способы задания функций. Общее понятие отношения. Бинарные отношения и их свойства (рефлексивность, симметричность, транзитивность). Отношение эквивалентности и классы эквивалентности. Отношение порядка. Линейный порядок и частичный порядок. ([1, часть 2, кроме § 5, 6]; [2, разд. 1.1‒ 1.3]; [3, § 5.1, 13.1 – 13.3]).

Понятие множества относится к числу первичных, под которым понимается некоторая совокупность элементов, объединенных по какимлибо признакам. С множествами, их графическим изображением на диаграммах Венна студенты встречались ранее в курсах математического анализа и теории вероятностей. Там же рассматривались понятия

подмножества В (части данного множества А: В А ), пустого множества

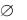(не содержащего ни одного элемента), дополнения А множества А (состоящего из всех элементов некоторого универсального множества2 U, не входящих в множество А). Определялись основные операции над множествами А и В: объединение А В (множество, состоящее из всех элементов множества А и В), пересечение А В (множество, состоящее из всех общих элементов А и В), разность А \ В (множество, состоящее из всех элементов множества А, не входящих в множество В).

1Учитывая, что учебный материал дисциплины недостаточно отражен в доступных для студента-заочника пособиях, содержание отдельных тем дается более подробно, чем это принято в методических пособиях (указаниях).

2Под универсальным множеством здесь понимается множество, включающее все множества, участвующие в рассматриваемой задаче.

5

В данном курсе вводится понятие прямого, или декартова, произведения множеств А и В, т.е. множество А В , элементы которого представляют всевозможные упорядоченные пары элементов множеств А и В (например, декартово произведение координатных осей Ох и Оу есть плоскость Оху).

Множество называется конечным, если содержит конечное число элементов и – бесконечным в противном случае.

Если между множествами А и В имеет место взаимно однозначное

множеств это означает, что в них одинаковое число элементов. В случае бесконечного множества мощность является обобщением понятия «число

состоят из одинаковых элементов), не эквивалентные (так как имеют разные мощности (число элементов)), причем множество Е включается в множество

D ( E D ). ►

Бинарным (двухместным) отношением множеств А и В называется

рефлексивность, симметричность, транзитивность ([1, часть 2, § 10]; [3, §13.3]). Бинарное отношение, для которого выполнены указанные три свойства, называется отношением эквивалентности, являющееся обобщением понятия равенства. Подмножества элементов, эквивалентные данному, называется его классом эквивалентности. Если бинарное

3 Множество называется счетным, если оно эквивалентно множеству натуральных чисел (его элементы можно перенумеровать).

6

и обществознанию: А С

Следовательно, только одну тройку по математике имеют 86–

–9–6–18=53 (чел).

в) Аналогично п. б) найдем число абитуриентов, имеющих только одну тройку по русскому языку:

71– (27–18) –(27–18) –18=35 (чел)

и по обществознанию:50–(24–

–18) – (27–18) –18=17 (чел). Всего абитуриентов, имеющих только одну тройку, равно 53+35+17=105

(чел). Решение задачи легко иллюРис. 1 стрируется на диаграмме Венна.

(рис.1)►

Тема 2. Комбинаторика

Предмет комбинаторики. Правило суммы и правило произведения. Размещения, перестановки, сочетания без повторений и с повторениями. Биномиальные коэффициенты и соотношения для них. Задачи перечисления. Подсчет числа функций с конечными областями определения. ([1, часть 3]; [2, разд. 3.1]); [3, § 1.5]).

Комбинаторика – раздел математики, изучающий методы решения задач, связанных с выбором и расположением частей конечного множества, в частности, комбинаторных задач на подсчет числа различных комбинаций.

Студенты должны четко знать правила комбинаторики:

- правило суммы: если объект А1 может быть выбран n1 способами, А2 –

осуществлен n1 n2 способами.

Из множества n различных элементов могут быть образованы подмножества (комбинации) из m элементов 0 m n.

Если комбинации из n элементов по m отличаются, либо составом элементов, либо порядком их расположения (либо и тем и другим), то их называют размещениями. Число размещений из n элементов по m находятся по формуле:

(где n! 12 3 ...n ).

8

Если комбинации из n элементов по m отличаются только составом элементов, то их называют сочетаниями. Число сочетаний из n элементов по m находятся по формуле:

элементов, то их называют перестановками. Число перестановок из n элементов находится по формуле:

Pn n!

Пример 3. В первом туре конкурса участвуют 16 человек. Сколько существует различных исходов этого тура, при которых совпадают участники, занявшие призовые 1-е, 2-е и 3-е места, а также два участника, занявшие 15-е и 16-е места и выбывающие из дальнейшего участия в конкурсе?

Р е ш е н и е. Способы распределения участников, занявших 1-е, 2-е и 3-е места (из 16), отличаются как составом участников, так и их порядком; их число – число размещений А163 . Из оставшихся 16 3 13 участников два

выбывают из конкурса (порядок этих участников значения не имеет); их число – число сочетаний С132 . По правилу произведения (см. с. 8) получаем,

что число различных исходов первого тура конкурса, удовлетворяющих условию задачи, есть

Другой способ решения состоит в том, что общее число различных исходов первого тура с 16-ю участниками (без учета распределения тех или иных мест) равно числу перестановок P16 . Перестановки участников,

занявших места с 4-го по 14-е (т.е. 11 мест), а также 15-е и 16-е места (2 места) приводят к совпадающему в соответствии с условием исходу первого тура; их число (по правилу произведения) равно P11 Р2 . Значит, число различных исходов первого тура конкурса, удовлетворяющих условию, есть

являются одинаковыми, то их называют комбинациями (размещениями, сочетаниями, перестановками) с повторениями.

Соответствующие формулы таких комбинаций с повторениями, приведены в пособии ([1, часть 3]; [3, § 1.5]). Там же рассматриваются задачи на подсчет различных комбинаций [1, 1-ое практическое занятие]; [3, примеры 1.11 – 1.15].

9

Тема 3. Математическая логика

Основные понятия логики: высказывания и рассуждения. Основные логические операции и их свойства. Алгебра высказываний. Понятие о булевской алгебре; алгебра высказываний как интерпретация булевской алгебры. Логические функции и способы их задания – таблицы и формулы. Дизъюнктивные и конъюнктивные формы. Теорема о функциональной полноте. Исчисление высказываний. Понятие об алфавите, формулах, аксиомах, правилах вывода и основных теоремах исчисления высказываний. Логика предикатов. Предметная область и предметные переменные. Кванторы общности и существования. Свободные и связанные переменные. Эквивалентные соотношения в логике предикатов. Общезначимые и противоречивые формулы. Запись утверждений естественного языка в логике предикатов. Понятие об исчислении предикатов ([1, часть 1, кроме §

11]; [2, разд. 1.4,1.5]; [3, § 13.1 – 13.3]).

При изучении темы следует усвоить основные понятия алгебры логики: высказывание (предположение, которое может быть истинно или ложно, при этом логическая переменная х равна соответственно 1 или 0),

логические операции (логические связки) с помощью которых строятся новые высказывания, образующие формулы алгебры логики (алгебры высказываний), таблицы истинности таких высказываний.

Надо четко знать основные логические операции: отрицание высказывания Х (высказывание Х , которое истинно, когда Х ложно, и ложно, когда Х – истинно), конъюнкция (дизъюнкция) двух высказываний Х и Y

Логические операции высказываний тесно связаны с операциями над множествами. Отрицание высказывания соответствует дополнению

10