Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Финансовый университет при Правительстве РФ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Образец оформления контрольной работы Теория игр

.pdf

Скачиваний:

Добавлен:

24.03.2016

Размер:

382.95 Кб

Скачать

☆

Задание 1.

Найти нижнюю и верхнюю цену игры, платежная матрица которой имеет вид, приведенный ниже. Убедиться, что игра имеет седловую точку. Найти цену игры. Указать оптимальные стратегии каждого из игроков.

1	2	3	4
4	3	4	5

5	1	3	5	.


1	1	4	5

Решение. В каждой строке платежной матрицы найдем наименьший элемент, и запишем его справа от матрицы. В каждом столбце платежной матрицы найдем наибольший элемент, и запишем его снизу от матрицы. В результате получим таблицу

1	2	3	4	1
4	3	4	5	3
4	3	4	5	3
5	1	3	5	1

1	1	4	5	1
1	1	4	5	1
5	3	4	5

Нижняя цена игры max{1, 3, 1, 1} 3. Верхняя цена игрыmin{5, 3, 4, 5} 3. Так как нижняя и верхняя цены игры совпадают, то

рассмотренная игра является игрой с седловой точкой. Седловой точкой является элемент С22 . В задачах с седловой точкой цена игры V .

Таким образом, цена рассматриваемой игры V 3. Оптимальной (максиминной) стратегией игрока A является стратегия A2 , а игрока B

оптимальной (минимаксной) стратегией является стратегия B2 .

Ответ: V 3 , оптимальные стратегии A2 и B2 .

Задание 2.

Предприниматель А планирует начать выпуск изделий Т1 и Т2. Ожидаемая прибыль зависит от того, какой вид изделий Т1 или Т2 будет выпускать конкурент В. Если оба будут производить изделия Т1, то ввиду конкуренции А понесет убытки в X тыс. руб. Если оба будут производить Т2, то по той же причине А понесет убытки в Y тыс. руб. Если А будет производить Т1 а В – Т2, то прибыль А составит Z тыс. руб. Если А будет производить Т2, а В – Т1, то прибыль А составит T тыс. руб. Найти оптимальные стратегии каждого из предпринимателей.

X=200, Y=100, Z=900, T=700;

Решение. Платежная матрица игры имеет вид:

200		900
			.
	700	100
	700	100

Найдем нижнюю и верхнюю цену игры. В каждой строке платежной матрицы найдем наименьший элемент, и запишем его справа от матрицы. В каждом столбце платежной матрицы найдем наибольший элемент, и запишем его снизу от матрицы. В результате получим таблицу

200		900	200

	700	100	100
	700	100	100

700 900

Нижняя цена игры max{ 200, 100} 100 . Верхняя цена игрыmin{700, 900} 700. Так как нижняя и верхняя цены игры не совпадают,

то рассмотренная игра не имеет седловой точки. В случае многократно повторяющихся игр без седловой точки постоянное использование минимаксных стратегий становится невыгодным. В этом случае решение нужно искать в области смешанных стратегий.

		У игрока A в рассматриваемой задаче есть две чистые стратегии: A1 и
A2 . Смешанная стратегия игрока						A состоит в том, чтобы применять эти
чистые стратегии, чередуя их по случайному закону с частотами p1							и p2 .
Причем				p1 p2 1. Смешанную		стратегию игрока A обозначим	через
S			A	A
S	A		1	2	. Аналогичным образом определяется и смешанная стратегия
	A			p2
		p1		p2

игрока B . Ее обозначим через S		B	B	. Средний выигрыш V	при
игрока B . Ее обозначим через S	B	1	2	. Средний выигрыш V	при
	B		q2
		q1	q2

применении обоими игроками оптимальных стратегий называется ценой

игры. Значения p1 , p2 , V , q1 и q2

определяются выражениями

c22

c21

c11

c22

c12

c21

c11

c12

c11

c22

c12

c21

c11c22 c12c21

c22

c12

c11

c22

c12

c21

c11

c21

c11

c22

c12

c21

Подставляя в записанные выше формулы значения коэффициентов платежной матрицы задачи, находим

								p							100 700										800							8	,
								p																									,
									1			200			100 900 700										1900						19
												200			100 900 700										1900						19
								p	2						200 900							1100									11 ,

												200			100 900 700										1900						19
												200			100 900 700										1900						19
						V				200 ( 100) 900 700											61000											610			,
											200 100 900 700												1900								19
								q							100 900							1000									10 ,
								1
								1				200			100 900 700									1900							19
												200			100 900 700									1900							19
								q							200 700										900							9		.
								q	2			200			100 900 700										1900									.
									2																						19
																															19
Так как p p											8		11	1 и q			q			10					9		1,				то частоты найдены
				1			2			19		19			1			2	19				19
										19		19							19				19
правильно. Таким образом, предпринимателю																						A выгодно реализовать обе
стратегии A1 и A2 , чередуя выпуск изделий Т1 и Т2 по случайному закону с
частотами		8		и		11		.		Гарантированная прибыль																при				этом составит								610		.
частотами	19			и		19		.		Гарантированная прибыль																при				этом составит								19		.
	19					19																																19
Предпринимателю B выгодно реализовать свои стратегии B1																																					и B2 с
частотами	10		и		9	.
частотами			и			.
	19			19
																	A1					A2									A1					A2		610
													Ответ: S						8		11					, S			10						9		, V	610	.
													Ответ: S						8		11					, S			10						9		, V		.
																A												B										19

																	19				19										19				19
																	19				19										19				19

Задание 3.

Предприятие имеет две стратегии рыночного поведения, тогда как его конкурент имеет четыре таких стратегии. Прибыль (в у.д.е.), которую получит предприятие при условии, что оно изберет стратегию i (i = 1, 2), а его конкурент стратегию j (j = 1, 2, 3, 4), равна aij. Платежная матрица для каждого варианта приведена ниже. Требуется графическим способом найти оптимальные смешанные стратегии предприятия и конкурента, а также цену игры оптимальную прибыль предприятия.

	1	5	9	3

	6	3	2
				7
Решение. Проведем через точку			(1, 0)		координатной плоскости Oxy
прямую l , перпендикулярную оси абсцисс.					Для каждой из стратегий B j
проведем прямую b j , соединяющую точку					(0, a1 j ) на оси Oy	с точкой
(1, a2 j ) на прямой l (см. рис.).		Затем		строим ломаную, звенья		которой

образуют отрезки построенных прямых, имеющие наименьшие ординаты. В

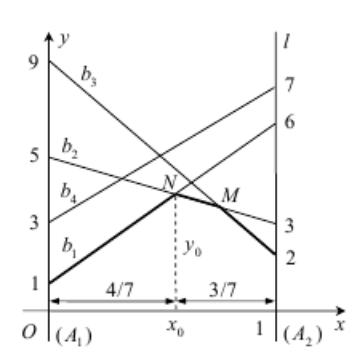
рассматриваемой задаче это ломаная 1NM 2. Среди вершин построенной ломаной находим ту, которая имеет наибольшую ординату. В данном случае это точка N . Она и определяет оптимальное решение задачи.

В точке N пересекаются прямые b1 и b2 , уравнения которых имеют вид: y 1 5x и y 5 2x .

														4			27
Вычислив				координаты				точки					N		,				,				получаем								оптимальную
Вычислив				координаты				точки					N		,				,				получаем								оптимальную
														7			7
						A1		A2																	27
стратегию игрока A : S						3		4		, и цену игры V															27			.
стратегию игрока A : S						3		4		, и цену игры V																		.
					A																					7

						7		7
						7		7
Так как точка N является пересечением прямых b1																													и b2 , то полезными
стратегиями игрока B будут стратегии B1 и B2 . Частоты их применения
найдем, зная, что выигрыш равен цене игры, если игрок																															B применяет
оптимальную стратегию, а игрок											A – любую из своих полезных стратегий,
например,		стратегию				A1 .	В			этом случае приходим к уравнению
q 5(1 q )			27	, решив которое							находим				q					2		,		q					5	. Таким образом,
1	1	7															1	7								2			7
		7																7											7
																			B1							B2
оптимальная стратегия игрока B имеет вид S																					2						5			B3	B4 .
																B													0		0
																B
																			7								7
									A1			A2							B1							B2				B3		27
				Ответ: S						3		4		,	S						2						5			B3	B4 , V	27	.
				Ответ: S						3		4		,	S						2						5		0		B4 , V	7	.
							A										B												0		0	7
							A										B
										7			7						7								7

Задача 4.

Нефтяная компания собирается построить в районе крайнего севера нефтяную вышку. Имеется 4 проекта A1 , A2 , A3 и A4 . Затраты на

строительство (млн. руб.) зависят от того, какие погодные условия будут в

период строительства. Возможны четыре варианта погоды S1 , S2 , S3					и S4 .
Используя	критерии	Вальда, максимального	оптимизма,	Гурвица	(при
0,6),	Сэвиджа	и Лапласа, выбрать	оптимальный	проект	для

строительства. Матрица затрат имеет вид:

2	19	7	8
6	10	7	9
6	10	7	9
6	12	15	5

9	14	8	7
9	14	8	7

Решение.

1. Критерий Вальда. Данный критерий основывается на принципе максимального пессимизма, то есть на предположении, что скорее всего произойдет наиболее худший вариант развития ситуации и риск наихудшего варианта нужно свести к минимуму. Для применения критерия нужно для каждой альтернативы выбрать наихудший показатель привлекательности (наименьшее число в каждой строке матрицы выигрышей) и выбрать ту альтернативу, для которой этот показатель максимальный. По сути дела критерий Вальда определяется максиминной стратегией.

С учетом сказанного находим

			2	19	7	8	2
			6	10	7	9	6
			6	10	7	9	6
			6	12	15	5	5

			9	14	8	7	7
			9	14	8	7	7
Таким	образом,	наилучшим				из	наихудших	показателей

max{2, 6, 5, 7} 7 обладает альтернатива A4 .

2.Критерий максимального оптимизма. Данный критерий предполагает, что произойдет такое развитие ситуации, которое будет наиболее благоприятным. В соответствии с критерием принимается альтернатива, соответствующая максимальному элементу матрицы выигрышей. Для применения критерия нужно для каждой альтернативы выбрать наилудший показатель привлекательности (наибольшее число в каждой строке матрицы выигрышей) и выбрать ту альтернативу, для которой этот показатель максимальный.

С учетом сказанного находим

2	19	7	8	19
6	10	7	9	10
6	10	7	9	10
6	12	15	5	15

9	14	8	7	14
9	14	8	7	14

Таким образом, наилучшим из наилудших показателейmax{19, 10, 15, 14} 19 обладает альтернатива A1 .

3. Критерий Гурвица. Рекомендует использовать стратегию, которой

соответствует	максимум	функции		полезности		каждой из альтернатив,
определяемой по формуле					) max a				0,6
определяемой по формуле		max min a (1			) max a			. Положим	0,6
		i	j	ij		j	ij
и найдем функции полезности для каждой альтернативы
		0,6 2 (1 0,6) 19 8,8,
		0,6 6 (1 0,6) 10 7,6 ,
		0,6 5 (1 0,6) 15 9,0 ,
		0,6 7 (1 0,6) 14 9,8 .
Так как	max{8,8, 7,6, 9,0, 9,8} 9,8 ,				то	преимуществом обладает

альтернатива A4 .

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, которая позволила бы не допустить чрезмерно высоких потерь, к которым она может привести. Вначале находится матрица рисков, элементы которой

находятся по формуле rij max aij aij , где max aij – максимальный элемент
			i							i
в	исходной матрице. Оптимальная						стратегия определяется выражением

min max r .
i		j	ij
		С учетом сказанного находим наибольшее значение элементов
исходной матрицы в каждом столбце
				2		19	7	8
				6		10	7	9
				6		10	7	9
				6		12	15	5		.

				9		14	8	7
				9		14	8	7
				9		19	15	9
		Затем строим матрицу рисков
					7	0	8	1
					3	9	8	0
					3	9	8	0
					3	7	0	4	.
					3	7	0	4

					0	5	7	2
					0	5	7	2

Находим наибольшее значение элементов в каждой строке матрицы рисков

7	0	8	1	8
3	9	8	0	9
3	9	8	0	9
3	7	0	4	7 .

0	5	7	2	7
0	5	7	2	7

Определяем наименьшее значение найденных максимальных значений min{8, 9, 7, 7} 7 . Таким образом, преимуществом обладают альтернативы

A3 и A4 .

5. Критерий Лапласа. Данный критерий основан на предположении, что каждый вариант развития ситуации равновероятен. Поэтому, для принятия решения, необходимо рассчитать среднеарифметическое значение показателей привлекательности по каждому «состоянию природы». Выбирается та альтернатива, для которой это значение максимально. Соответственно находим.

2 19 7 8

9 ,

6 10 7 9

8 ,

6 12 15 5

9,5 ,

9 14 8 7

9,5 ,

max(9, 8, 9,5, 9,5) 9,5 .

Таким образом, согласно критерию Лапласа преимуществом обладают

альтернативы A3 и A4 .

Сведем полученные результаты в таблицу.

Критерий

Число

Максималь

Решение

принятых

Вальда

ного

Гурвица

Сэвиджа

Лапласа

решений

оптимизма

Исходя из данных приведенных в таблице, следует рекомендовать к реализации проект A4 .

Ответ: проект A4 .

Задача 5.

Найти решение матричной игры, сведя ее к задаче линейного программирования.

3	2	1	5
5	2	3	2

1	2	4	5

Решение. Рассмотрим задачу со стороны игрока A . Так как он имеет

три стратегии,					то введем три переменные x1 , x2 ,					x3 , пропорциональные
вероятностям					использования		чистых		стратегий.	Тогда	цена игры
V		1			, а частоты использования чистых					стратегий	найдем по

	x	x		x
1			2	3
формулам				p1 x1V , p2 x2V ,		p3 x3V .			Значения x1 , x2 , x3 находим из
решения задачи линейного программирования, которая имеет вид:
						x1 x2 x3 min ,
						3x1 5x2 x3 1;
							2x1 2x2		23 1;
							2x1 2x2		23 1;

						x1 3x2 4x3 1;
						5x 2x		2	5x 1;
							1	2	3
							xi	0 .

Решение поставленной задачи линейного программирования получено с использованием надстройки «Поиск решения» пакета Excel и имеет вид:


	x1	x2			x3
	0,333333	0		0,166667
	1	1		1				0,5
	3	5		1			1,166667			1
	2	2		2				1		1
	1	3		4				1		1
	5	2		5				2,5		1

	V=	2
	p1=	0,6667
	p2=	0,0000
	p3=	0,3333
Таким образом, цена игры равна 2, а смешанная стратегия игрока A
				A1		A2		A3
записывается следующим образом S				1		A2		2	.
записывается следующим образом S				1				2	.
			A			0

				3				3
				3				3

Рассмотрим задачу со стороны игрока B . Так как он имеет четыре стратегии, то введем четыре переменные y1 , y2 , y3 , y4 . Тогда цена игры не

изменится, а частоты использования чистых стратегий найдем по формулам q1 y1V , q2 y2V , q3 y3V , q4 y4V . Значения y1 , y2 , y3 , y4 находим из решения задачи линейного программирования, которая имеет вид::

y1 y2 y3 y4 max ,

3y1 2 y2 y3 5y4 1;5y1 2 y2 3y3 2 y4 1;

y1 2 y2 4 y3 5y4 1; y j 0 .


	y1		y2				y3		y4
		0		0,5				0			0
		1			1			1			1		0,5
		3			2			1			5			1		1
		5			2			3			2			1		1
		1			2			4			5			1		1

	V=				2
	q1=				0
	q2=				1
	q3=				0
	q4=				0
Из приведенного				решения следует, что игроку B следует
придерживаться стратегии B2 .
						A1		A	A3				B		B B B			, V 2.
	Ответ: S					1		2	2		, S			1	2	3	4	, V 2.
				A				0				B		0	1	0	0
						3		0		3				0	1	0	0
						3				3

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.03.2016175.62 Кб7Оборотка и журнал операций.doc
#
11.07.201966.05 Кб1образец выполнения теор части1.doc
#
11.07.201970.14 Кб1образец выполнения теор.части.doc
#
11.07.201967.58 Кб2образец выполнения теор.части2.doc
#
08.11.201884.48 Кб6образец выполнения теор.части3.doc
#
24.03.2016382.95 Кб69Образец оформления контрольной работы Теория игр.pdf
#
13.03.201522.21 Кб16Образец протокола ССТ.docx
#
26.08.201937.58 Кб4ОБРАЗОВАНИЕ СТЕПЕНЕЙ СРАВНЕНИЯ.docx
#
13.03.2015566.48 Кб9Образцы базовых задач по ЛА.pdf
#
13.03.2015117.76 Кб4образцы практ ФК ФМ.doc
#
13.03.201574.24 Кб66Образцы решения экзаменационных задач I.doc