Контрольная работа №4

1. По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование строительных организаций региона по объему выполненных работ. Результаты представлены в таблице.

Объем работ, млн. руб.	Менее 56	56-60	60-64	64-68	68-72	Более 72	Итого
Число организаций	9	11	19	30	18	13	100

Найти:

1. Границы, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организаций региона;

2. Вероятность того, что доля всех строительных организаций, объем работ которых составляет не менее 60 млн. руб., отличается от доли таких организаций в выборке не более чем на 0,05 (по абсолютной величине);

3. Объем бесповторной выборки, при котором те же границы для среднего объема выполненных работ (см. п. а)) можно гарантировать с вероятностью 0,9876.

Решение:

Находим выборочную среднюю: .

– объем выборки

, , , , , – середины интервалов

Находим выборочную дисперсию:

Найдем границы, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организаций региона.

По таблицам значений функции Лапласа находим:

Интервальные для оценки средней находятся по формулам:

,

где

,

тогда

.

Получаем:

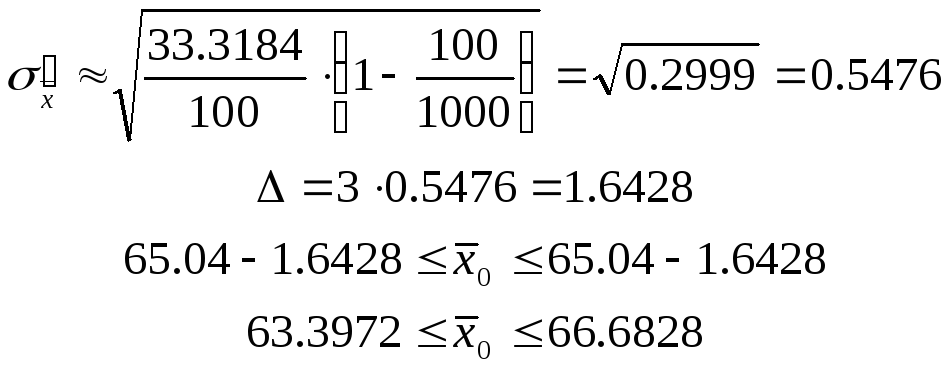
Найдем вероятность того, что доля всех строительных организаций, объем работ которых составляет не менее 60 млн. руб., отличается от доли таких организаций в выборке не более чем на 0,05 (по абсолютной величине). Для этого находим среднюю квадратическую ошибку выборки для доли:

– для бесповторной выборки

Здесь – выборочная доля строительных организаций, объем работ которых составляет не менее 60 млн. руб.

– объем генеральной совокупности (в данном случае – 1000)

Находим вероятность того, что доля всех строительных организаций, объем работ которых составляет не менее 60 млн. руб., отличается от доли таких организаций в выборке не более чем на 0,05 (по абсолютной величине)

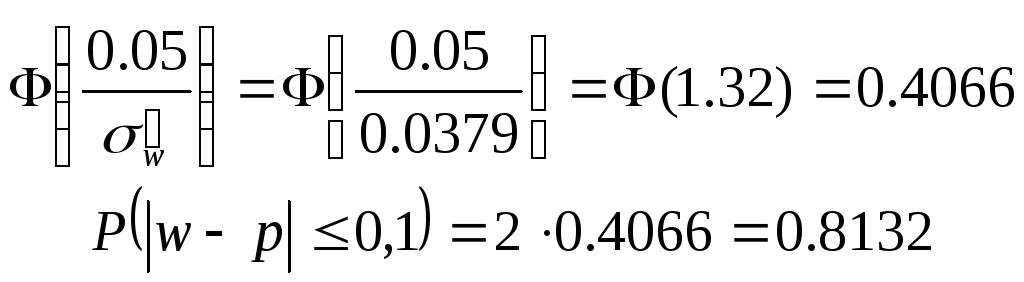
Найдем объем бесповторной выборки, при котором те же границы для среднего объема выполненных работ (см. п. а)) можно гарантировать с вероятностью 0,9876.

Объем бесповторной выборки определяется по формуле:

О твет:

1. Границы, в которых с вероятностью 0,9973 заключен средний объем выполненных работ всех строительных организаций региона:

2. Вероятность того, что доля всех строительных организаций, объем работ которых составляет не менее 60 млн. руб., отличается от доли таких организаций в выборке не более чем на 0,05 (по абсолютной величине) равна 0.8132;

3. Объем бесповторной выборки, при котором те же границы для среднего объема выполненных работ (см. п. а)) можно гарантировать с вероятностью 0,9876 равен 71 организации.

2. По данным задачи 1, используя -критерий Пирсона, на уровне значимости 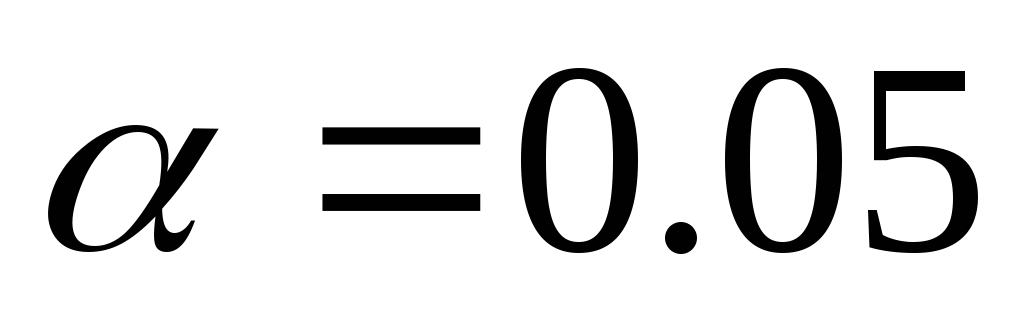проверить гипотезу о том, что случайная величина 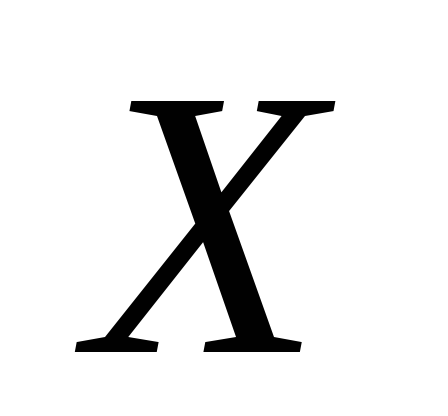– объем выполненных работ – распределена по нормальному закону.

Решение:

Используем данные, полученные в предыдущем задании:

В качестве дисперсии нормального закона распределения следует взять исправленную выборочную дисперсию, но т.к. количество наблюдений в данном случае 100, достаточно велико, то подойдет и .

Случайная величина распределена по нормальному закону, если ее функция распределения имеет вид

,

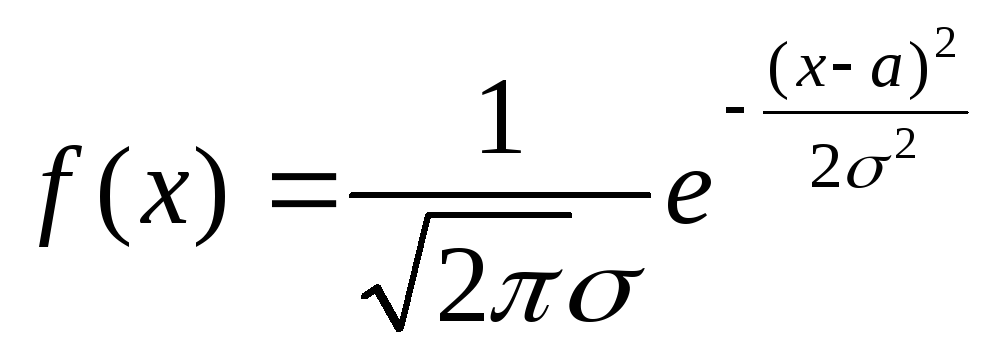где – математическое ожидание, – среднее квадратическое отклонение.

Подставляем ,

Таким образом, теоретическое нормальное распределение имеет вид:

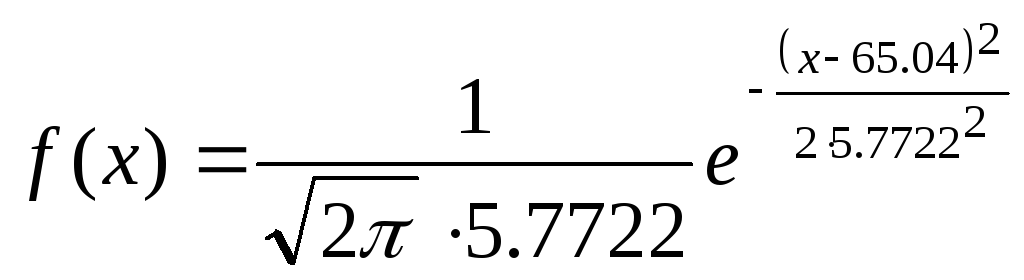
Для расчета вероятностей попадания случайной величины в интервал используем функцию Лапласа:

В данном случае получаем:

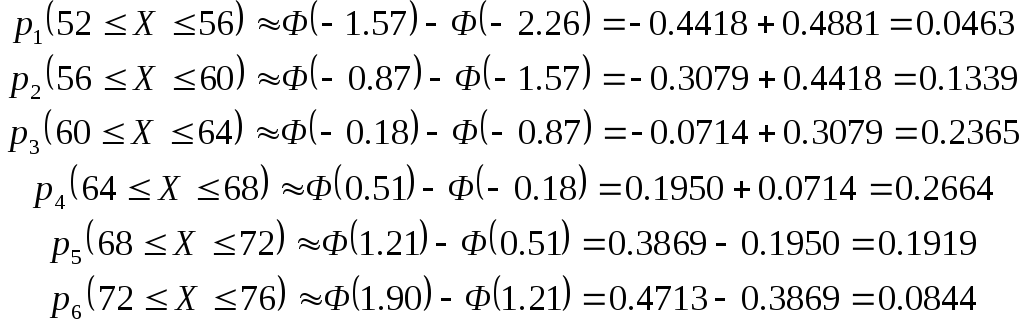
Составим таблицу:

	Интервал	Эмпирические частоты	Вероятности	Теоретические частоты
1	52-56	9	0.0463	4.63	19.0969	4.1246
2	56-60	11	0.1339	13.39	5.7121	0.4266
3	60-64	19	0.2365	23.65	21.6225	0.9143
4	64-68	30	0.2664	26.64	11.2896	0.4238
5	68-72	18	0.1919	19.19	1.4161	0.0738
6	72-76	13	0.0844	8.44	20.7936	2.4637
		100	0.9594	95.94

Таким образом, значение статистики .

Определим количество степеней свободы по формуле: .

– число интервалов ()

– число параметров закона распределения (в нормальном распределении )

.

Соответствующее критическое значение статистики

Поскольку , то гипотеза о нормальном распределении с параметрами не согласуется с опытными данными.

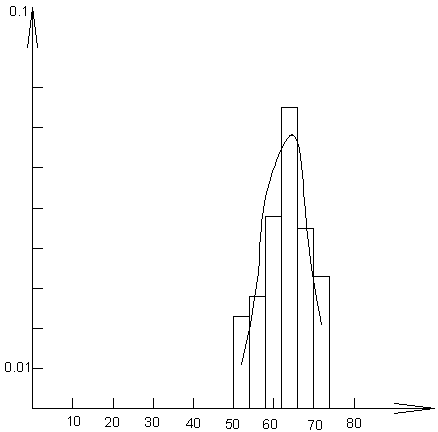
Ниже показана гистограмма эмпирического распределения и соответствующая нормальная кривая.