Лекции_Информатика

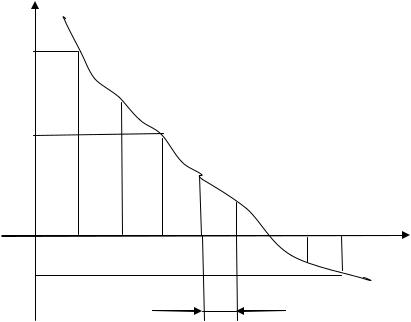
71

Рассмотренные выше циклические структуры характеризуются одной общей особенностью – во всех рассмотренных примерах заранее можно определить число повторений тела цикла. Задачи, где число повторений заранее неопределенно, приводят к так называемым циклам с неизвестным

(до начала цикла) числом повторений.

Пусть, например, надо определить интервал (a, b), внутри которого функция y=f(x) пересекает ось абсцисс (внутри этого интервала функция f(x) обращается в ноль, т. е. f(x)=0). На рис. 5.8 показано возможное решение поставленной задачи в форме соответствующего графика. Первоначально можно предположить, что искомый интервал может иметь границы a=x0 и b=x0+hx. Если в указанном интервале нет искомой точки, то искать ее следует в следующем интервале (a+hx , b+hx). Последовательный анализ интервалов продолжается до тех пор, пока не будет достигнут искомый результат. Необходимое условие того, что функция y=f(x) пересекает ось абсцисс, может быть записано в следующем виде: ya·yb<0, где ya = f(a); yb = f(b).

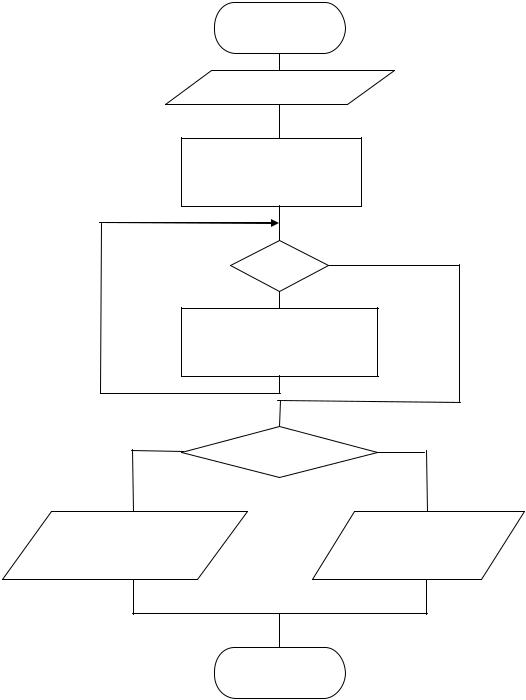
На рис. 5.9 приведена схема алгоритма нахождения интервала (a, b), с использованием оператора цикла с предусловием.

y

y0

y1

y2

Рис. 5.8 Нахождение интервала, внутри которого функция пересекает ось абсцисс

Условие продолжения цикла определено с помощью логической переменной v. Значение переменной v формируется из двух условий. С одной стороны выход из цикла возможен в тех случаях, когда найден искомый интервал (a, b), т. е. выполняется условие f(a)f(b)<0. С другой стороны, точка пересечения с осью абсцисс может отсутствовать, тогда выход из цикла осуществляется в результате достижения граничной (конечной) точки xn. Объединенное условие продолжения цикла

Переход к ОГЛАВЛЕНИЮ

72

Начало

Ввод x0, hx, xn

a:=x0; b:=x0+hx ya:=f(a); yb:=f(b)

Нет

v

Да

a:=a+hx; b:=b+hx ya:=f(a); yb:=f(b)

b>xn+hx/2

Конец

Рис. 5.9 Схема алгоритма определения интервала, внутри которого функция пересекает ось абсцисс

Переход к ОГЛАВЛЕНИЮ

73

5.2. Алгоритм вычисления суммы бесконечного ряда

Характерным примером итерационных циклов является задача вычисления суммы бесконечного ряда:

s tn (x),

n 0

где tn(x) – слагаемое, зависящее от параметра x (в общем случае) и номера n. Вычисляемая последовательность

Для контроля погрешности можно использовать последовательность

где tn(x) = sn(x) – sn-1(x) – слагаемые ряда n.

limtn (x) 0 .

n

Условие выхода из итерационного цикла (справедливо при знакопеременном ряде {tn(x)}):

| tn ( x ) | < .

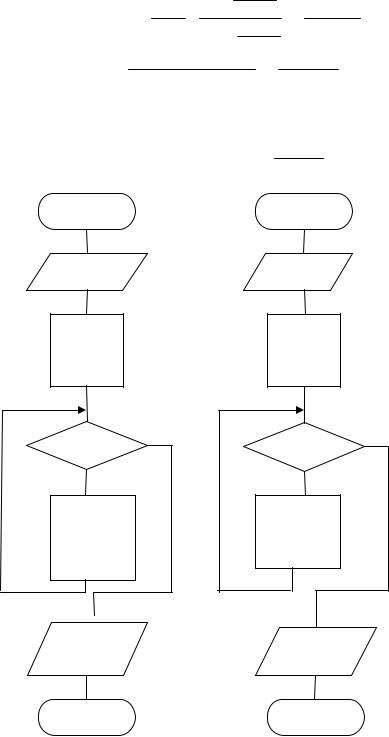
Алгоритм вычисления бесконечной суммы является модификацией одного из алгоритмов вычисления конечной суммы. Если применение рекуррентных формул нецелесообразно, то вычисления будут наиболее эффективными, если каждое слагаемое определять по общей формуле и полученные значения накапливать в некоторой переменной. Общий вид схемы алгоритма, реализующего вычисление бесконечной суммы с погрешностью с помощью цикла с предусловием, показан на рис. 5.10, а.

Если для вычисления слагаемых используются рекуррентные соотношения

то общая схема итерационного алгоритма для вычисления бесконечной суммы показана на рис. 5.10, б.

Например, тригонометрическая функция sin(x) может быть представлена в виде бесконечной суммы

Теперь можно определить

Переход к ОГЛАВЛЕНИЮ

74

Начальное значение слагаемого находим по формуле

Рис. 5.10 Схемы алгоритмов итерационных циклов, реализующих вычисление бесконечной суммы

Переход к ОГЛАВЛЕНИЮ

75

5.3. Алгоритмы нахождения корней уравнений.

Решение алгебраических уравнений численными методами состоит из двух этапов:

–отделение корней, т. е. отыскание достаточно малых интервалов (a, b), в каждом из которых заключен один и только один корень;

–вычисление (уточнение) корня с заданной погрешностью.

Для отделения корней можно использовать алгоритм, схема которого приведена на рис. 5.9. На втором этапе используется один из известных алгоритмов уточнения значения корня. При этом любой из известных алгоритмов реализует вычисления в соответствии с итерационным циклом. Рассмотрим более подробно эти алгоритмы.

5.3.1. Метод итераций

Пусть задано уравнение f(x) = 0, имеющее один-единственный корень х на интервал (a, b), т. е. a ≤ x ≤ b.

Уравнение f(x) = 0 представим в виде, необходимом для реализации

метода итерации x = φ(x).

Если в интервале (a, b) выполняется неравенство |φ'(x)| ≤ q < 1, то

метод итерации применим к исходному уравнению, и приведет к уточнению корня с заданной точностью (процесс итерации сходится).

Приведение исходного уравнения f(x) = 0 к форме x = φ(x).может быть выполнено разными способами. Один из них сводится к следующему. Предположим, что 0 ≤ m ≤ f(x) ≤ M при a ≤ x ≤ b (если f(x) < 0, то достаточно уравнение f(x) = 0 умножить почленно на -1), тогда уравнение

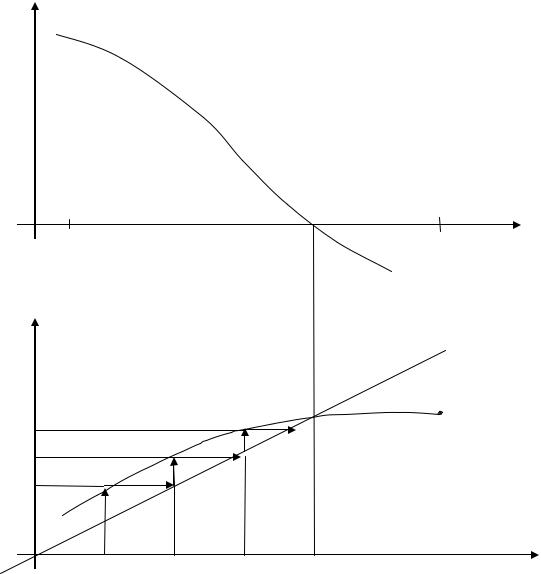
На рис. 5.11,а показан геометрический смысл первоначального уравнения f(x)=0. На этом рисунке точка х* является искомой. В результате тождественных преобразований исходного уравнения f(x)=0 к требуемому виду получаем геометрический смысл итерационного метода. На рис. 5.11,б искомый корень х* определяет точку пересечения двух функций: у

= х и у =φ(х).

Метод итерации состоит из последовательности следующих шагов: выбираем любое значение х = х0 из интервала (a, b), вычисляем φ(х0) и приравниваем его к новому значению корня x1:

Далее этот процесс повторяется так, что k-я итерация состоит в вычислении

xk (xk 1 ).

Переход к ОГЛАВЛЕНИЮ

76

Погрешность εk на k-й итерации удовлетворяет неравенству

Процесс итерации проводим до тех пор, пока погрешность εk будет больше заданной погрешности ε. На рис. 5.11,б прямые со стрелками показывают итерационное движение вычислительного процесса к искомому значению х*.

В алгоритме метода итераций вычисляется последовательность значений

х0, х1, х2, …, хn, …

по формуле xn = φ(xn-1). Данная последовательность сходится к величине х*. Условие продолжения цикла

|xn – xn-1| > ε,

т.е. вспомогательная последовательность для контроля погрешности:

|x1 – x0|, |x2 – x1|, …, |xn – xn-1|, … .

Заметим, что в качестве вспомогательной можно использовать последовательность

|f(x0)|, |f(x1)|, |f(x2)|, …, |f(xn)| … ,

которая сходится к нулевому значению.

y

y=f(x)

Рис. 5.11. Геометрическая иллюстрация метода итераций

y

y= x

y= φ(x)

φ(x2) φ(x1)

φ(x0)

77

Поэтому условием продолжения цикла с предусловием может быть неравенство

f (xn ) .

Пусть, например, необходимо найти с погрешностью ε = 10-4 корень уравнения

Приведем исходное уравнение к виду

Для определения x0 применим графический метод отделения корней, а именно построим график функций

Нетрудно убедиться, что корень (точка пересечения этих графиков) принадлежит к отрезку [0, 1]. Поэтому

5.3.2. Метод половинного деления

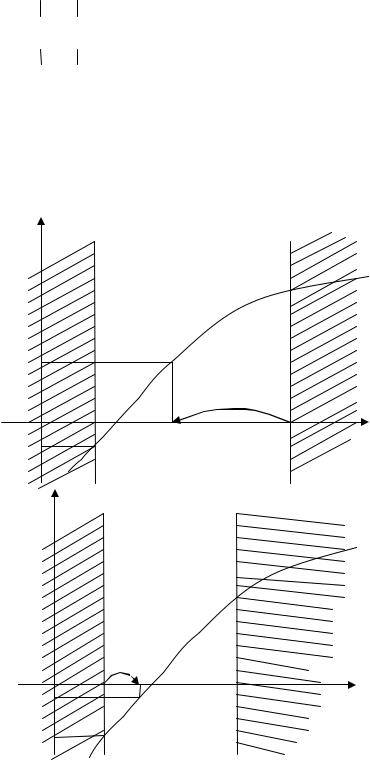
Метод половинного деления является более универсальным, всегда приводит к искомому результату, хотя и требует большого объема вычислений. Для нахождения корня уравнения f(x)=0, принадлежащего отрезку [a, b], делим отрезок пополам z = (a+b)/2 (см. рис. 5.12,а). Далее рассмотрим значения функции y = f(x) в точках x = a и x = z. Если значения f(a) и f(z) разных знаков, т. е. f(a) f(z) < 0, то исходный отрезок [a, b] уменьшим в два раза путем переноса точки x = b в точку x = z. Новый отрезок [a, b] вновь делим пополам (см. рис. 5.12,б) и так как f(a) f(z) < 0, то переносим точку x = a в точку x = z, уменьшая [a, b] в два раза. Повторяем указанную процедуру до тех пор, пока длина отрезка, содержащего корень, не станет меньше заданной погрешности ε. Любое значение является искомым значением корня, однако на практике в качестве корня выбирают середину отрезка, т. е. x = (a+b)/2.

При организации итерационного цикла вычисляется последовательность отрезков

[a0, b0], [a1, b1], …, [an, bn], … ,

для которой

Для контроля точности вычисления корня можно использовать следующую последовательность значений

b0 a0 ; b1 a1 ; ...; bn an ; ... ,

Переход к ОГЛАВЛЕНИЮ

78

поэтому условие выхода из цикла

или условие продолжения цикла

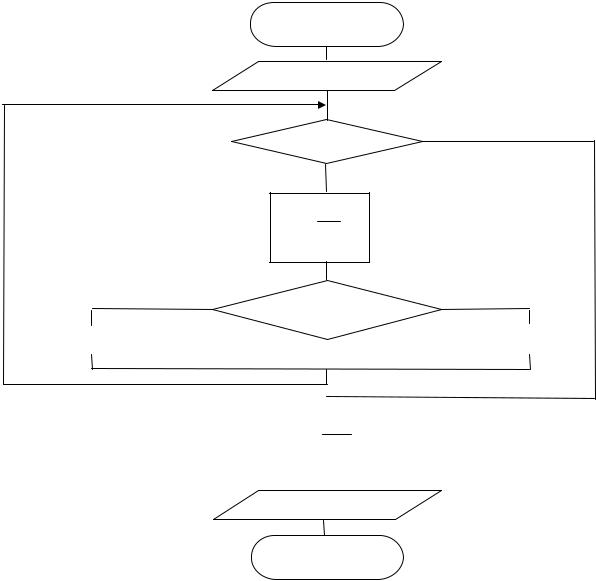
Схема алгоритма уточнения корня алгебраического уравнения методом половинного деления приведена на рис. 5.13. В результате выполнения такого алгоритма выводится значение корня (с заданной погрешностью), а также значение функции f(x), которое очень близко к нулевому значению и может быть использовано для контроля правильности полученного результата.

y

y=f(x)

f(z)

f(a)

a)

y

y=f(x)

f(a)

b)

Рис. 5.12 Графическая иллюстрация метода половинного деления

Переход к ОГЛАВЛЕНИЮ

79

Начало Ввод a, b, ε

Нет

|b-a| ≥ ε

Да

z : a b z

f(z)f(a) < 0

Вывод x, f(x)

Конец

Рис. 5.13 Схема алгоритма уточнения корня методом половинного деления

5.3.3. Метод касательных

Для обеспечения сходимости метода касательных (метода Ньютона) необходимо, чтобы производные f' (x) и f" (x) были определены,

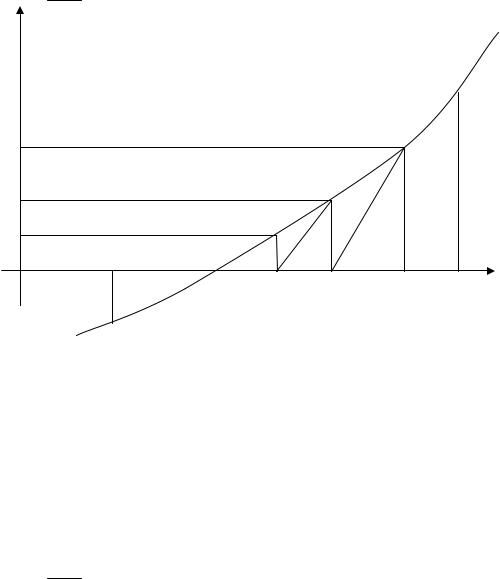
непрерывны и сохраняли постоянные знаки на отрезке [a, b]. На рис. 5.14 представлена геометрическая интерпретация метода Ньютона.

Выберем некоторую точку x0 на отрезке [a, b] и проведем касательную к кривой y=f(x) в точке P0(x0, y0). Ее уравнение

y = y0 + f' (x0)(x–x0), где y0 = f(x0).

Переход к ОГЛАВЛЕНИЮ

80

Новое приближение корня х1, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.

y

y=f(x

y0

y1 y2

Рис. 5.14 Геометрическая интерпретация метода касательных

Выберем некоторую точку x0 на отрезке [a, b] и проведем касательную к кривой y=f(x) в точке P0(x0, y0). Ее уравнение

y = y0 + f' (x0)(x–x0),

где y0 = f(x0).

Новое приближение корня х1, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.

Проведя касательную через точку P1(x1, y1), получим второе приближение корня x2. Вычисление приближений корня по формуле

продолжается до выполнения неравенства

xn xn 1 ,

где ε – абсолютная погрешность определения корня уравнения. Начальное приближение х0 выбирают таким образом, чтобы

выполнялось условие

f (x0 ) f ''(x0 ) 0.

В противном случае сходимость метода Ньютона не гарантируется. На практике выбирают x0 = a или x0 = b, в зависимости от того, в какой из

Переход к ОГЛАВЛЕНИЮ