Лекции_Информатика

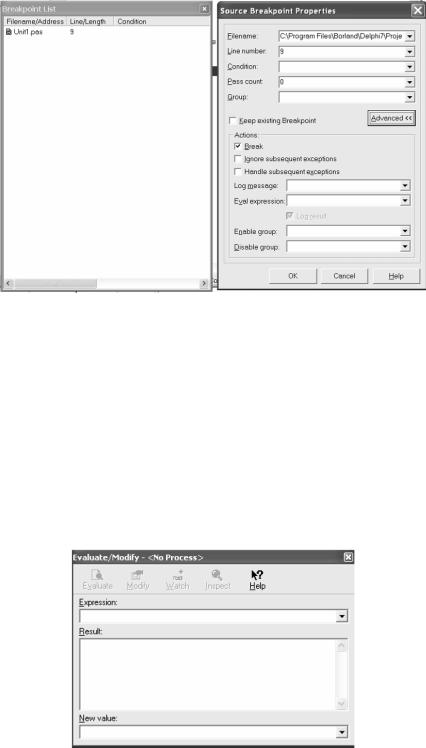
61

Handle subsequent exceptions – после установки этого переключателя отменяется действие предыдущего переключателя и возобновляется обработка возможных исключений;

Log message –можно указать произвольное сообщение, связанное с точкой останова;

Eval expression – можно вычислить некоторое выражение и поместить его результат в это сообщение.

Окно свойств точек останова

(6)Группировка точек прерывания

ВDelphi имеется возможность объединения точек останова в группы. Для этого используется все то же окно (рис. 7.4): в строке Group следует указать имя группы, к которой принадлежит точка, а в строках Enable group и Disable group соответственно разрешить или запретить действие всех точек останова, относящихся к соответствующей группе.

(7)Вычисление выражений и изменение значений

С помощью окна Evaluate/Modify опции Run можно узнать значение любого выражения или установить в переменную другое значение. Это окно вызывается в режиме отладки после нажатия Ctrl+F7.

Окно просмотра изменения значений

Переход к ОГЛАВЛЕНИЮ

62

Встроке Expression можно написать имя переменной или интересующее вас выражение. После щелчка по кнопке Evaluate в поле Result появится текущее значение переменной (выражения). Если в Expression содержится имя переменной, одновременно становится доступной кнопка Modify, а в строке New value повторяется текущее значение переменной. Если изменить эту строку и нажать Modify, в переменную будет помещено новое значение, которое и будет использоваться при дальнейшем прогоне программы (если определяется значение выражения, кнопка Modify и строка New value будут недоступны).

Можно использовать дополнительные кнопки этого окна Watch и Inspect. Если щелкнуть по первой из них, выражение (переменная) из окна Evaluate будет перенесено в окно наблюдений Watch, щелчок по второй отображает выражение (переменную) в специальном окне Inspect.

(8)Ведение протокола работы программы

Вряде случаев бывает неудобно или невозможно пользоваться пошаговой отладкой программ. В таких ситуациях могут помочь контрольные точки, которые не прерывают работу программы, а лишь помещают некоторую информацию в специальный файл трассировки. Для реализации такой точки следует раскрыть окно Run|Add Breakpoint|Source Breakpoint (рис. 7.1), убрать флажок в переключателе Break и написать сообщение в строке Log message. Можно также в строке Eval expression указать выражение, которое будет вычислено и вместе с сообщением помещено в протокол работы программы. Этот протокол можно просмотреть в любой момент (в том числе и после завершения прогона программы) с помощью опции View|Debug Windows|Event Log.

Переход к ОГЛАВЛЕНИЮ

63

Глава 5. Лекция 5

5.1. Алгоритмы вычисления определенных интегралов.

Основу численных методов вычисления определенных интегралов составляет их геометрический смысл. Определенным интегралом

b s f (x)dx

a

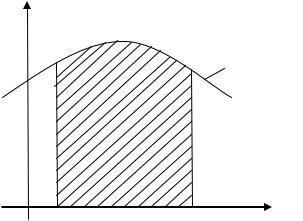
называют площадь криволинейной трапеции, ограниченную подынтегральной кривой, осью абсцисс и ординатами f(a) и f(b). На рис. 5.1 данная площадь заштрихована.

y

y=f(x)

Рис. 5.1 Геометрический смысл определенного интеграла

При численном интегрировании подынтегральную функцию заменяют более простой, для которой вычисление указанной площади производится в соответствии с достаточно простыми формулами, и искомый интеграл вычисляют приближенно с определенной точностью.

5.1.1. Метод прямоугольников.

Наиболее простым методом численного интегрирования является метод, основанный на применении формулы прямоугольников. В этом случае подынтегральную функцию/кривую заменяют прямой, а формула для вычисления площади прямоугольника известна. Для повышения точности вычислений участок интегрирования [a, b] разбивается на n равных частей. Далее берутся значения подынтегральной функции в левых (или правых) концах полученных участков. При этом подынтегральная функция f(x) на

Переход к ОГЛАВЛЕНИЮ

64

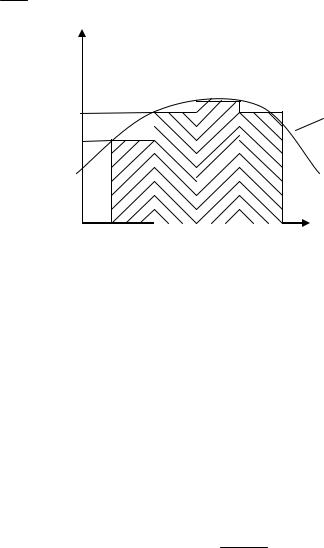
отрезке [a, b] заменяется ступенчатой кривой (см. рис. 5.2), и приближенное значение интеграла определяется суммой площадей прямоугольников

Аналогичная формула прямоугольников получится и в том случае, если брать для интегральной суммы значения функции f(x) не в левых, а в правых концах участков разбиения:

В результате расчетов по формулам «слева» и «справа» получается приближенное значение интервала (с недостатком или с избытком), которое может отличаться от действительного на некоторую величину, называемую ошибкой ограничения. Эта ошибка определяется величиной остаточного члена ряда Тейлора:

R h(b a) f ' (v), a v b. 2

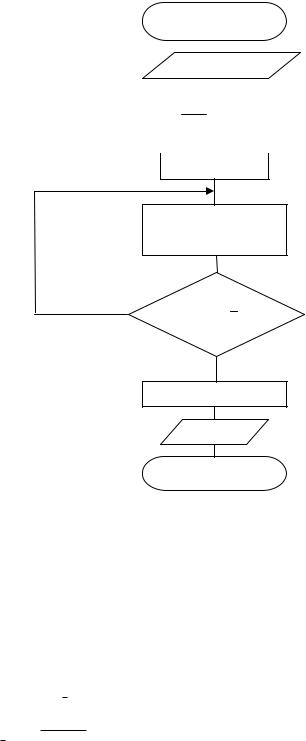
В качестве примера на рис. 5.3 приведена схема алгоритма, реализующего вычисления по формуле прямоугольников «слева». Увеличение числа участков разбиения n приводит к повышению точности вычисления интеграла. Следует обратить внимание также на формирование условия выхода из цикла на рис. 5.3, добавление половины шага h в условие необходимо для избежания возможного сравнения на равенство двух вещественных значений x и b–h.

Определение интеграла по формуле средних

Переход к ОГЛАВЛЕНИЮ

65

x:=a

s:=s+f(x)

x:=x+h

Нет

x b h2

Да

s:=s h

s

Конец

Рис. 5.3 Алгоритм вычисления определенного интеграла методом прямоугольников

С целью повышения точности вычислений по методу прямоугольников значение подынтегральной функции целесообразно взять не на концах участков, а в их середине. В результате получим формулу средних:

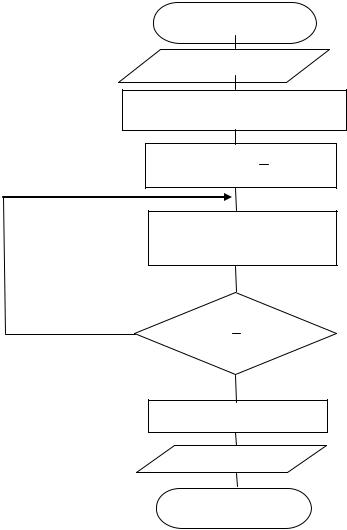
Данный метод вычисления определенного интеграла обеспечивает более высокую точность при равном n по сравнению с формулами прямоугольников. Формулу средних рекомендуется использовать для достаточно гладких функций f(x), не содержащих высокочастотных колебаний на отдельных интервалах интегрирования. На рис. 5.4 показана схема алгоритма вычисления интеграла по формуле средних.

Переход к ОГЛАВЛЕНИЮ

66

Начало

Ввод a, b, n

h : b a ; s : 0 n

s:=s+f(x) x:=x+h

Нет

Да

s:=s h

Вывод s

Конец

Рис. 5.4 Алгоритм вычисления определенного интеграла по формуле средних.

5.1.2. Формулы Ньютона-Котеса

Если подынтегральную функцию заменить каким-либо интерполяционным многочленом, то получим квадратурные формулы вида:

где хк – выбранные узлы интерполяции; Ak – коэффициенты, которые зависят от выбранных узлов, но не зависят от вида функции f(x); R – остаточный член, определяющий максимальную ошибку при использовании квадратурной формулы; k=0, 1, …, n.

Разбивая отрезок интегрирования [a, b] на n равных частей системой

точек

xk = x0+kh; k=0, 1, …, n; x0=a; xn=b

Переход к ОГЛАВЛЕНИЮ

67

и вычисляя подынтегральную функцию в полученных узлах

yk=f(x); k=0, 1, …, n,

получают квадратурные формулы для равноотстоящих узлов. Эти формулы называют формулами Ньютона-Котеса. Наиболее удобны при численном интегрировании интерполяционные многочлены невысоких порядков, при использовании которых получают достаточно простые составные формулы.

(1) Формула трапеций.

Формула трапеций получается в случае использования интерполяционного многочлена 1-го порядка:

Для нахождения приближенного значения определенного интеграла по формуле трапеций можно использовать алгоритм, схема которого представлена на рис. 5.5.

Ошибка ограничения для метода трапеций больше, нежели чем для других формул Ньютона-Котеса, но его привлекательность заключается в простой реализации. Кроме того, незначительное усложнение алгоритма позволяет существенно снизить погрешность вычислений, поэтому формула трапеций достаточно часто используется (в сочетании с другими формулами).

Например, в случае аппроксимации подынтегральной функции интерполяционным многочленом Эрмита получают формулу Эйлера:

Остаточный член этой формулы свидетельствует о том, что небольшая добавка к формуле трапеций существенно повышает ее точность.

В последней формуле значения производных можно заменить двусторонними разностями

В результате формула Эйлера превращается в формулу Грегори, но общий порядок точности понизится с четвертого до третьего.

(2) Формула парабол (Симпсона)

Используя интерполяционный многочлен 2-го порядка (параболу) получают формулу численного интегрирования – формулу Симпсона:

Переход к ОГЛАВЛЕНИЮ

68

Рис. 5.5 Алгоритм вычисления определенного интеграла по формуле трапеций

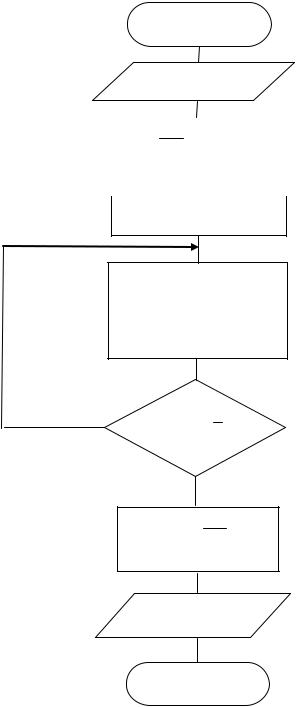
На рис. 5.6 показана схема алгоритма, реализующего вычисления по формуле парабол. При реализации формулы число узлов обязательно нечетно, т. е. число участков разбиения интервала интегрирования должно быть четным: n=2m. В алгоритме использован прием, при котором число повторений цикла уменьшается в два раза, т. е. дважды реализуется

Переход к ОГЛАВЛЕНИЮ

69

модификация параметра цикла, что уменьшает время выполнения алгоритма. Метод Симпсона считается одним из наиболее применяемых методов численного интегрирования, обеспечивающим достаточно хорошую точность вычислений.

Вывод s

Конец

Рис. 5.6 Алгоритм вычисления определенного интеграла по формуле Симпсона

Переход к ОГЛАВЛЕНИЮ

70

(3) Формула Ньютона (правило трех восьмых)

Более высокую точность вычисления обеспечивает интерполирование подынтегральной функции полиномом третьей степени. В результате получают формулу Ньютона (правило трех восьмых):

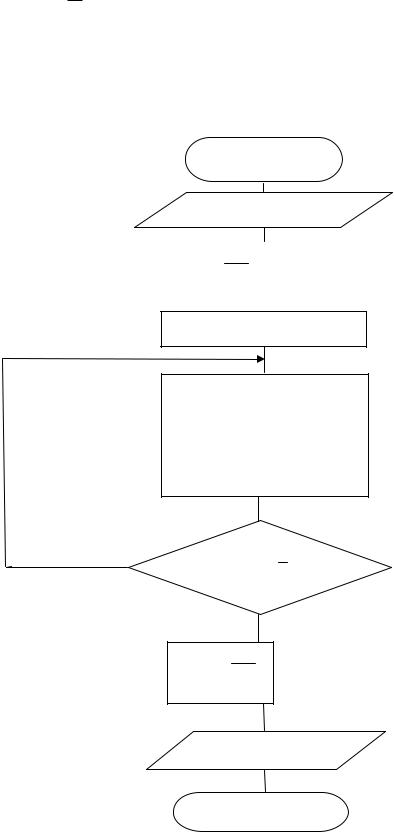
правилу трех восьмых показана на рис. 5.7 Практическое применение нашли также четвертая, пятая и шестая формулы Ньютона-Котеса, однако их использование приводит к более громоздким схемам.

Начало Ввод a, b, n

Переход к ОГЛАВЛЕНИЮ