
Глава 1
.pdf
нормальные формы. Дизъюнктивной нормальной формой (ДНФ) булевой функции f называется реализующая f формула, являющаяся дизъюнкцией элементарных конъюнкций. В отличии от СДНФ совершенная дизъюнктивная нормальная форма функции f определяется неоднозначно, т.е. f может иметь несколько реализующих ее ДНФ. Минимальной дизъюнктивной нормальной формой функции f называется ДНФ, содержащая минимальное число символов переменных среди всех ДНФ функции f. Получить ДНФ можно из СДНФ при помощи эквивалентных преобразований.
Пример 1.4.3. Найдем минимальную ДНФ импликации. Сделаем это преобразуя ее СДНФ при помощи приведенных в предыдущем параграфе равенств:
x y x y xy xy x y xy xy xyx y y y x x x y .
Так как импликация существенно зависит от двух переменных, то очевидно, что ее любая ДНФ содержит символы обеих переменных. Таким
образом, формула x y будет минимальной ДНФ импликации. 
3.Конъюнктивные нормальные формы. Для любого x = (x1,…, xn)
илюбого ( 1,..., n ) дизъюнкция
|
|
d x |
x 1 ... x n , |
|
|
|
|
|
|
1 |
n |
|
|
булевых степеней 1,..., n |
переменных x1,…, xn называется |
|||||
элементарной |
|
дизъюнкцией, |
ассоциированной |
с |
булевым набором |
|
( 1,..., n ) . |
Если все i |
равны единице, |
то |
дизъюнкция d x |
||
называется монотонной. Для функции d x |
справедливо соотношение |
|||||
d |
0, если α и σ-противоположные наборы, |
|||||
|
|
|
|
|
|
|
|
|
1, в остальных случаях. |
|
|
|
|
Пусть f(x1, …, xn) - произвольная булева функция. Представим отрицание f в виде совершенной дизъюнктивной нормальной формы:

|
x |
|
|
|
x 1 |
... x n |
|
|
|
|
,..., |
|
, |
f |
,..., x |
V |
f |
1 |
n |
||||||||
1 |
n |
|
1,..., n |
1 |
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
где дизъюнкция берется по всем таким наборам , что f() = 0. Взяв отрицания от обоих частей равенства и применив законы двойственности, видим, что для функции f справедливы равенства
|
|
|
|
|
x 1 ... x n . |
|
|||
f x ,..., x |
x 1 |
... x n |
|
(1.4.3) |
|||||
1 |
n |
1 |
n |
|
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
в которых дизъюнкция и конъюнкция берутся |
по |
всем тем |
наборам |
||||||
( 1,..., n ) , для которых f() |
= 0. Формула, |
стоящая в правой части |
|||||||
равенства (1.4.3), называется совершенной конъюнктивной нормальной формой (СКНФ) функции f(x1, …, xn) .
Пример 1.4.4. Дизъюнкция x y двух переменных x и y сама является своей совершенной конъюнктивной нормальной формой. Совершенные конъюнктивные нормальные формы других функций двух переменных приведены ниже:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y = (x y)( x y)(x y ), |
x y (x y)(x y) , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x y x y , |
x y = (x y)(x y) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x y (x y)(x y)(x y) , |
x | y x y . |
||||||||||||||||||||||
Конъюнктивной нормальной формой (КНФ) булевой функции f
называется реализующая f формула, являющаяся конъюнкцией элементарных дизъюнкций. Как и в случае дизъюнктивных нормальных форм КНФ называется минимальной, если она содержит минимальное число переменных среди всех КНФ функции f.
Пример 1.4.5. Найдем минимальную КНФ стрелки Пирса. Сделаем это преобразуя ее СКНФ. Легко видеть, что
x y (x y)(x y)(x y) (x y xy)(x y) x y .

Так как стрелка Пирса существенно зависит от двух переменных, то очевидно, что ее любая КНФ содержит символы обеих переменных. Таким
образом, формула x y будет минимальной КНФ стрелки Пирса. 
4. Алгебраическая нормальная форма. Для любого x B его
алгебраической степенью (или просто степенью) называется функция
|
1, |
при 0; |
x |
|
|
|
при 1. |
|
|
x, |
|
|
|
|
Для любого x = (x1, …, xn) и любого ( 1,..., n ) произведение
Px x 1 ... x n ,
1 n
степеней 1,..., n переменных x1, …, xn называется булевым одночленом, ассоциированным с булевым набором ( 1,..., n ) . Вес этого набора называется степенью одночлена (1.4.4) и обозначается deg P (x).
Булевы одночлены от переменных x1, …, xn естественным образом нумеруются номерами ассоциированных булевых наборов - номером одночлена (1.4.4) является величина | |. Далее для обозначения одночлена P (x) будем также использовать обозначение p (x) или просто p ,
если из контекста понятно от каких переменных зависит рассматриваемый одночлен. Для функции P (x) справедливо соотношение
|
|
|
|
|
|
1, |
если |
|
P |
p |
|
|
|
|
|
|
|
|
|
|
|
|
(1.4.5) |
|||
|
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0, |
в остальных случаях. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Пример 1.4.6. Ниже приведены все булевы наборы длины два и ассоциированные с этими наборами одночлены от двух переменных:
= (0, 0), |
| | = 0, |
p |
x0x0 |
1 1 1; |
||
|
|
0 |
1 |
2 |
|
|
= (0, 1), |
| | = 1, |
p |
x0x1 |
1 x |
x ; |
|
|
|
1 |
1 |
2 |
2 |
2 |
= (1, 0), |
| | = 2, |
p |
x1x0 |
x 1 x ; |
||
|
|
2 |
1 |
2 |
1 |
1 |
= (1, 1), |
| | = 3, p |
x1x1 |
x |
x . |
|
|
3 |
1 |
2 |
1 |
2 |
Легко видеть, что deg p0 = 0, deg p1 = deg p2 = 1 и deg p3 = 2. 
Теорема 1.4.2. Каждая булева функция f(x1, …, xn) единственным образом представляется в виде
f x |
,..., x |
|
|
x 1 |
... x n p |
, |
(1.4.6) |
|
1 |
n |
|
1,..., n |
1 |
n |
|
|
|
где p {0, 1}. Формула (1.4.6) называется алгебраической нормальной формой функции f или ее многочленом Жегалкина.
Доказательство. Прежде всего покажем, что каждая булева функция реализуется не более чем одним многочленом Жегалкина. Сделаем это методом от противного. Предположим, что некоторую булеву функцию f(x1, …, xn) реализуют два различных многочлена Жегалкина h1 и h2. Тогда
h1(x) h2(x) = f(x) f(x) = 0. С другой стороны, так как h1 h2, то многочлен h1 h2 содержит хотя бы один ненулевой одночлен.
Следовательно, тождественный нуль реализуется многочленом h1 h2. В многочлене h1 h2 выберем одночлен минимальной степени, если таких одночленов несколько, то выберем любой. Пусть p - выбранный одночлен. Легко видеть, что если одночлен p принадлежит многочлену h1 h2, то
либо , либо . Из (1.4.5) следует, что p| |( ) = 1 и p| | ( ) = 0 для любого большего или несравнимого с . Поэтому , значение многочлена h1 h2 на любом наборе большем или несравнимым с равно единице. Противоречие. Следовательно, каждая булева функция реализуется не более чем одним многочленом Жегалкина.
Для окончательного доказательства теоремы осталось найти число различных многочленов от n переменных. Так как каждый одночлен, зависящий от n переменных (не обязательно существенно), однозначно определяется булевым набором длины n, то очевидно, что число одночленов равно 2n. Каждый одночлен либо входит, либо не входит в
многочлен. Следовательно, число различных многочленов равно 22n , т.е. многочленов столько же, сколько и булевых функций, зависящих от n переменных. Так как каждая булева функция реализуется не более чем одним многочленом Жегалкин, то для каждой функции найдется реализующий ее многочлен. Теорема доказана.
Итак, каждая булева функция f единственным образом представляется в виде многочлена Жегалкина. Степенью функции f, обозначается через deg f, называется максимальная степень одночленов, входящих в ее многочлен Жегалкина.
Пример 1.4.7. Методом неопределенных коэффициентов найдем многочлен Жегалкина дизъюнкции двух переменных. Для этого дизъюнкцию x1 x2 представим в виде многочлена
x1 x2 a bx1 cx2 dx1x2 |
(1.4.7) |
с неизвестными коэффициентами a, b, c и d. Подставляя в левую и правую части (1.4.7) нули вместо переменных x1 и x2, получаем, что a = 0. Полагая далее x1 = 1, x2 = 0, находим a b = 1. Подстановки x1 = 0, x2 = 1 и x1 = x2 = 1, дают, соответственно, a c = 1 и a b c d = 1. Таким образом, для определения четырех неизвестных коэффициентов получили систему из четырех уравнений. Решая эту систему, легко находим a = 0, b = c = d = 1. Следовательно, x1 x2 = x1 x2 x1x2. 
Задачи
1.4.1.Разложить по первой переменной функцию:
a)x1 x2 x3, b) 1 x1 x2 x3, c) x1x2 x3.
1.4.2.Показать, что каждая булева функция трех переменных имеет
симметрическую подфункцию двух переменных.
1.4.3.Найти число различных дизъюнктивных нормальных форм над множеством переменных x1, …, xn.
1.4.4.Показать, что любая ДНФ функции x1 … xn состоит из 2n-1 элементарных конъюнкций.
1.4.5.Показать, что любая ДНФ функции x1 … xn состоит из
n 2n 1 символов переменных.
1.4.6.Найти число различных конъюнктивных, нормальных форм над множеством переменных x1, …, xn.
1.4.7.Показать, что любая КНФ функции x1 … xn состоит из 2n-1 элементарных дизъюнкций.
1.4.8.Показать, что любая КНФ функции x1 … xn состоит из
n2n 1 символов переменных.
1.4.9.Найти число одночленов степени k от n переменных.
1.4.10.Найти число одночленов четной степени от n переменных.

1.4.11.Найти число одночленов степени n2 от n переменных.
1.4.12.Пусть p - одночлен степени k от n переменных. Найти
p(x) , где сумма берется по всем булевым наборам длины n.
1.4.13.Найти многочлен Жегалкина функции f если:
a)f = x | y, b) f = x y, c) f = x y.
1.4.14.Найти многочлен Жегалкина функции f если:
a) f = x y z, b) f = (x y) z, c) f = (x y)&(y z).
1.5. Замкнутые классы булевых функций
Пусть R - произвольное множество булевых функций. Замыканием множества R называется множество всех функций, которые можно реализовать формулами в базисе R. Замыкание множества R будем обозначать через [R].
Множество булевых функций R называется (функционально) замкнутым множеством, если оно совпадает со своим замыканием, т.е. R = [R].
Рассмотрим пять важнейших замкнутых множеств в P2. Часто рассматриваемые ниже замкнутые множества называются так же замкнутыми классами.
1. Будем говорить, что функция f(x1, …, xn) сохраняет нуль, если
f(0, …, 0) = 0.
Множество, состоящее из всех булевых функций сохраняющих нуль, обозначается через T0. Легко видеть, что функции 0, x, x&y, x y и x y
принадлежат T0, а функции 1, x , x y, x | y, x y и x y не принадлежат
T0.
Так как тождественная функция сохраняет нуль, и для любых сохраняющих нуль функций f0, f1, …, fk справедливо равенство
f(0, ...,0) = f0(f1(0, ..., 0), …, fk(0, ..., 0)) = f0(0, ..., 0) = 0,
т.е. реализуемая формулой f0(f1, …, fk) функция f так же сохраняет нуль, то легко видеть, что множество T0 замкнуто.

Любой булев вектор длины 2n с первой нулевой компонентой будет
вектором значений функции из T0. Поэтому, в T0 содержится ровно 22n 1 функций из P2(n). Множество T0 P2(n) будем обозначать через T0(n).
2. Будем говорить, что функция f(x1, …, xn) сохраняет единицу, если
f(1, …, 1) = 1.
Множество, состоящее из всех булевых функций сохраняющих единицу, обозначается через T1.
Легко видеть, что функции 1, x, x & y, x y, x y и x y принадлежат
T1, а функции 0, x , x y, x | y и x y не принадлежат T1. Доказательство замкнутости множества T1 аналогично доказательству замкнутости
множества T0. Также легко видеть, что в T1 содержится ровно 22n 1 функций из P2(n). Множество T1 P2(n) будем обозначать через T1(n).
3. Будем говорить, что булева функция f(x1, …, xn) является
двойственной к функции g(x1, …, xn), если
f x1,..., xn y x1,..., xn .
Функцию двойственную к функции f будем обозначать через f*. Легко видеть, что (f*)* = f для любой булевой функции f. Из законов двойственности следует, что (x & y)* = x y и (x y)* = x & y. Функция f называется самодвойственной, если f = f*. Множество, состоящее из всех самодвойственных булевых функций, обозначается через S.
Самодвойственными являются функции x, x , x1 x2 x3.Среди булевых функций, существенно зависящих ровно от двух переменных, нет ни одной самодвойственной функции.
Докажем замкнутость множества самодвойственных функций. Пусть f0, f1, …, fk - произвольные самодвойственные функции. Рассмотрим новую функцию f = f0(f1, …, fk). Так как добавление фиктивной переменной оставляет самодвойственную функцию самодвойственной, то без ограничения общности будем полагать, что все функции fi зависят от одних и тех же переменных x1, …, xn. Тогда
fx1,..., xn f0 f1 x1,..., xn ,..., fk x1,..., xn
f0 f 1 x1,..., xn ,..., f k x1,..., xn

f 0 f1 x1,..., xn ,..., fk x1,..., xn f x1,..., xn .
Следовательно, функция f - самодвойственная. Таким образом, множество S замкнуто.
Так как каждая самодвойственная функция на противоположных наборах принимает противоположные значения, то для определения любой самодвойственной функции достаточно задать ее значения только на
половине из 2n наборов. Следовательно, в S содержится ровно 22n 1 функций из P2(n). Далее множество самодвойственных функций, зависящих от n переменных, будем обозначать через S(n).
4. Функция f(x1, …, xn) называется линейной, если степень ее многочлена Жегалкина не превосходит единицу, т.е.
f(x1, …, xn) = 1x1 … nxn 0,
где i - булевы постоянные. Множество, состоящее из всех линейных булевых функций, обозначается через L. Очевидно, что среди функций из
P2(2) линейными являются только 0, 1, x, x , x y и x y. Непосредственно из определения линейной функции следует замкнутость множества L.
Так как каждая булева функция однозначно определяется коэффициентами своего многочлена Жегалкина, а у каждой линейной функции все коэффициенты при одночленах степени два и выше равны нулю, то легко видеть, что в L содержится ровно 2n+1 функций из P2(n). Далее множество L P2(n) будем обозначать через L(n).
5. Функция f(x1, …, xn) называется монотонной, если
f 1,..., n f 1,..., n
для любых наборов 1,..., n и 1,..., n таких, что . Множество, состоящее из всех монотонных булевых функций, обозначается через M. В P2(2) монотонными являются функции 0, 1, x, x&y
и x y.
Докажем замкнутость множества монотонных функций. Пусть f0, f1, …, fk - произвольные монотонные функции. Очевидно, что добавление фиктивной переменной оставляет монотонную функцию монотонной. Поэтому без ограничения общности будем полагать, что все функции fi
зависят от одних и тех же переменных x1, …, xn. Пусть , - такие наборы из Bn, что . Рассмотрим новую функцию f = f0(f1, …, fk). Так как fi( )
fi(), то (f1(), …, fk( )) (f1(), …, fk()), и поэтому
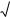
f f0 f1 ,..., fk f0 f1 ,..., fk f .
Следовательно, функция f - монотонная. Таким образом, множество M замкнуто.
В отличие от множеств T0(n), T1(n), S(n) и L(n), мощности которых легко были найдены выше, точное число монотонных функций в P2(n) при больших n не известно. Поэтому здесь без доказательства приведем только формулу для асимптотики логарифма числа монотонных функций в P2(n). Обозначим множество монотонных функций n переменных через M(n). Тогда
|
|
|
|
|
n |
|
|
|
2n |
||
|
M n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||||
log2 |
|
|
n |
|
|
|
|
|
. |
||
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
n / 2 |
|||
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
Пример 1.5.1. Найдем мощность множества L(n) S(n). Из определений линейных и самодвойственных функций следует, что если f L(n) S(n), то для f справедливы равенства
f x 0 1x1 ... n xn 1 0 1 x1 1 ... n xn 1
0 1x1 ... n xn 1 1 ... n f x 1 1 ... n
Откуда немедленно следует, что 1 ... n 1. Таким образом,
линейная функция будет самодвойственной тогда и только тогда, когда она существенно зависит от нечетного числа переменных. Следовательно,
|L(n) S(n)| = 2n.
Задачи
1.5.1.Найти число монотонных функций в P2(3).
1.5.2.Показать, что функция двойственная к монотонной так же будет монотонной.
1.5.3.Будет ли множество симметрических функций замкнутым?
|
|
|
|
|
|
n |
|
1.5.4. Показать, что log2 |
|
M n |
|
|
n |
|
|
|
|
||||||
|
|
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
|
1.5.5. Показать, что log2 |
|
M n |
|
|
n |
|
|
|
|
||||||
|
|
|
log2 n. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1.5.6. Найти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a) |
|
|
|
|
L n T0 n T1 n |
|
; |
|
|
|
|
b) |
|
|
|
|
L n T0 n T1 n |
|
|
; |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
L n M n T0 n |
|
; |
|
|
|
|
d) |
|
S n T0 n \ L n |
|
; |
||||||||||||||
c) |
|
|
|
|
||||||||||||||||||||||||||
e) |
|
|
|
S n T0 n T1 n L n |
|
; |
f) |
|
S n \ T0 n \ L n |
|
; |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
g) |
|
S n L n T0 n T1 n |
|
; |
h) |
|
L n \ S n \ M n |
|
. |
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
1.6. Критерий полноты системы булевых функций
Система булевых функций F = {f1, f2, …, fi , …} называется функционально полной, если любая булева функция может быть реализована формулой в базисе F. Так как каждая булева функция реализуется своими совершенной дизъюнктивной нормальной формой и алгебраической нормальной формой, то системы функций {&, , } и {&,, 1} будут полными. Для установления полноты других систем можно воспользоваться следующей теоремой.
Теорема 1.6.1. Пусть F и G - системы булевых функций, система F полная и каждая ее функция реализуется формулой в базисе G. Тогда G -- - полная система.
Доказательство. Покажем, что произвольная булева функция h может быть реализована формулой в базисе G. Сделаем это индукцией по глубине формул, реализующих булевы функции в базисе F. В основание индукции положим формулы нулевой глубины, т.е. переменные. Далее предположим, что любая функция, реализуемая в базисе F формулой глубины l, может быть реализована формулой в базисе G. Пусть h - произвольная булева функция, для которой существует реализующая ее в базисе F формула H глубины l. Тогда H = f(H1, …, Hk), где f F и H1, …, Hk формулы в базисе F. Очевидно, что d(Hi) < d(H) для каждого i из {1, …, k} и поэтому по предположению индукции реализуемые формулами H1, …, Hk функции h1, …, hk реализуются так же формулами H'1, …, H'k в базисе G. По условию теоремы функция f(y1, …, yk) реализуется формулой F в базисе G. В этой формуле каждую переменную yi заменим формулой
