
- •Исследование характеристик преобразования Гильберта
- •Реферат
- •Аннотация
- •Содержание
- •Обозначения и сокращения
- •Введение
- •Основная часть
- •1 Теоретическая часть
- •Практическая часть
- •2.2 Реализация модели преобразователя в среде MatLab. Формирование и анализ различных характеристик преобразователя Гильберта.
- •2.3 Анализ ско фазового шума при различных параметрах исходного сигнала и различных способах задания преобразователя Гильберта с помощью функции remez.
- •Заключение
- •Список использованных источников
Основная часть
1 Теоретическая часть
1.1 КИХ-фильтры
Учитывая, что фильтр Гильберта является частным случаем КИХ фильтров, сначала рассмотрим их.
КИХ-фильтр (фильтр с конечной импульсной характеристикой), называемый также нерекурсивным, - это фильтр, импульсный отклик которого содержит лишь конечное число ненулевых отсчетов. Такой импульсный отклик всегда абсолютно суммируем, и, следовательно, КИХ-фильтры всегда устойчивы. КИХ-фильтры имеют также то преимущество, что их работу легче понять как в одномерном, так и в многомерном случае.
Передаточная функция физически реализуемого цифрового фильтра с конечной импульсной характеристикой (КИХ-фильтра) может быть представлена в виде
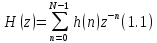
, где h(n) – импульсная характеристика. При замене в (1.1) z = ejw получим частотную характеристику КИХ-фильтра в виде
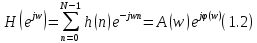
где
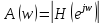 – амплитудно-частотная характеристика
(АЧХ) фильтра,
– амплитудно-частотная характеристика
(АЧХ) фильтра,
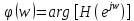 – фазо-частотная характеристика (ФЧХ)
фильтра.
– фазо-частотная характеристика (ФЧХ)
фильтра.
Фазовая задержка фильтра определяется как
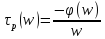
Групповая задержка фильтра определяется как
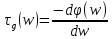
Отличительной способностью КИХ-фильтров
является возможность реализации у них
постоянных фазовой и групповой задержек,
т.е. линейной ФЧХ:
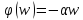 ,
при соблюдении этого условия сигнал,
проходящий через фильтр, не искажает
своей формы. Условия, обеспечивающие
линейную ФЧХ КИХ-фильтра: импульсная
характеристика фильтра должна быть
симметричной относительно точки
,
при соблюдении этого условия сигнал,
проходящий через фильтр, не искажает
своей формы. Условия, обеспечивающие
линейную ФЧХ КИХ-фильтра: импульсная
характеристика фильтра должна быть
симметричной относительно точки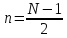 для нечетногоNи
относительно средней точки интервала
для нечетногоNи
относительно средней точки интервала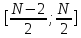 , гдеN– количество
отсчётов импульсной характеристики
данного КИХ-фильтра, см. Рисунок 1.1.
, гдеN– количество
отсчётов импульсной характеристики
данного КИХ-фильтра, см. Рисунок 1.1.
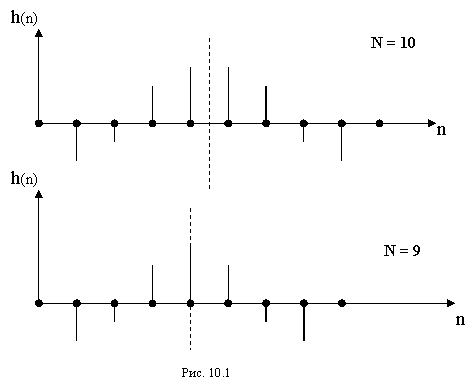
Рисунок 1.1 – Импульсные характеристики КИХ-Фильтров
Преобразование Гильберта
Преобразование Гильберта для любого произвольного сигнала представляет собой идеальный широкополосный фазовращатель, который осуществляет поворот начальных фаз всех частотных составляющих сигнала на угол, равный 90о(сдвиг на/2). Применение преобразования Гильберта позволяет выполнять квадратурную модуляцию сигналов, в каждой текущей координате модулированных сигналов производить определение огибающей и мгновенной фазы и частоты сигналов.
Прямое преобразование Гильберта произвольной действительной функции x(t),
-< t <,
результат которого будем отображать
со знаком тильды над индексом исходной
функции, задается сверткой x(t) с функцией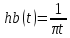
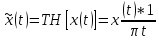
, где TH сокращение отTransform Hilbert.
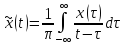
Функция
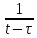 называетсяядром преобразованияГильберта. Обратное преобразование
Гильберта определяется выражением:
называетсяядром преобразованияГильберта. Обратное преобразование
Гильберта определяется выражением:
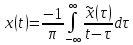
Преобразование Фурье от функции
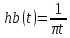 :
:
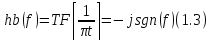
, где TFсокращение отTransformFourier.
Фурье-образ функции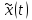 :
:
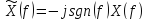
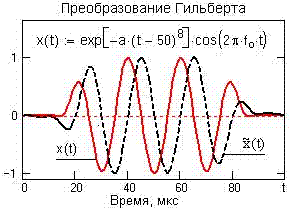
Рисунок 1.2.1 – Исходный и преобразованный сигнал
Изменение спектра сигналов при выполнении
преобразования Гильберта. На рисунке
1.2.1 приведено преобразование
радиоимпульсного сигнала x(t) с несущей
частотой foв сигнал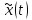 во временной области непосредственно
через операцию свертки с функцией
во временной области непосредственно
через операцию свертки с функцией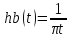 . Сигнал x(t) является односторонним
каузальным. Спектр сигнала содержит
реальную и мнимую составляющие, т.е.
может быть записан в виде
. Сигнал x(t) является односторонним
каузальным. Спектр сигнала содержит
реальную и мнимую составляющие, т.е.
может быть записан в виде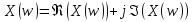 .
Эти составляющие для сигнала x(t) показаны
непрерывными кривыми на
.
Эти составляющие для сигнала x(t) показаны
непрерывными кривыми на
рисунке 1.2.2.
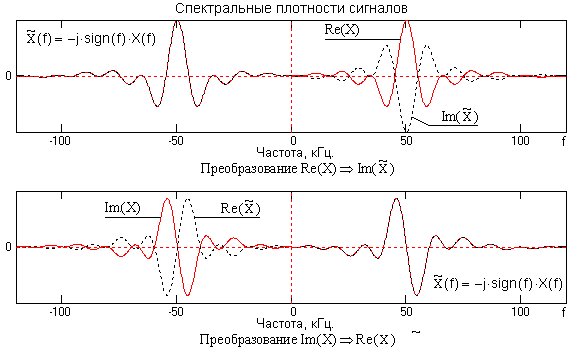
Рисунок 1.2.2. – Спектральные составляющие сигнала x(t)
При выполнении преобразования
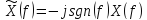 реальная и мнимая части спектра X(w)
умножаются на -jsgn(w).
Функция Re(X(w)) умножается
на 1 приw<0, на 0 приw=0
и на –1 приw>0, и тем самым
превращается в нечетную мнимую часть
Im(
реальная и мнимая части спектра X(w)
умножаются на -jsgn(w).
Функция Re(X(w)) умножается
на 1 приw<0, на 0 приw=0
и на –1 приw>0, и тем самым
превращается в нечетную мнимую часть
Im(![]() (w))
спектра
(w))
спектра![]() (w)
функции
(w)
функции![]() (t),
показанную пунктиром. Это означает, что
все косинусные гармоники сигнала,
которым соответствует реальная часть
спектра сигнала, превращаются в синусные
гармоники.
(t),
показанную пунктиром. Это означает, что
все косинусные гармоники сигнала,
которым соответствует реальная часть
спектра сигнала, превращаются в синусные
гармоники.
Аналогично на функцию –j sgn(w)
умножается и мнимая функция j Im(X(w)),
при этом сигнатурная функция инвертируется
(-j j = 1), что меняет знак левой части
функции Im(X(w)) – области
отрицательных частот, и превращает ее
в реальную четную часть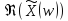 спектра
спектра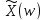 .
Синусные гармоники спектра сигнала
превращаются в косинусные гармоники.
.
Синусные гармоники спектра сигнала
превращаются в косинусные гармоники.
При выполнении преобразования гильберта
фазовый спектр сигнала ![]() (t)
(начальные фазовые углы всех гармонических
составляющих сигнала) сдвигается на
-90опри f > 0 и на 90опри f <
0 относительно фазового спектра сигнала
x(t).
(t)
(начальные фазовые углы всех гармонических
составляющих сигнала) сдвигается на
-90опри f > 0 и на 90опри f <
0 относительно фазового спектра сигнала
x(t).
Свойства преобразования Гильберта:
Линейность. ТН[ax(t)+by(t)]
= a![]() (t)+b
(t)+b![]() (t)
при любых постоянных значениях
коэффициентов а и b для любых произвольных
функций x(t) и y(t).
(t)
при любых постоянных значениях
коэффициентов а и b для любых произвольных
функций x(t) и y(t).
Сдвиг. ТН[x(t-a)]
= ![]() (t-a).
(t-a).
Преобразование константы, а в силу линейности преобразования, и постоянной составляющей сигнала, равно нулю. Это прямо следует из нечетности ядра преобразования Гильберта. Отсюда следует, что при преобразовании Гильберта из квадратурной составляющей исключается постоянная составляющая.
Свойство четности и нечетностиопределяется сдвигом всех гармоник
сигнала на/2, при
этом четные сигналы x(t) дают нечетные
сигналы![]() (t),
и наоборот. Это действительно и для
произвольных сигналов относительно их
четных и нечетных частей.
(t),
и наоборот. Это действительно и для
произвольных сигналов относительно их
четных и нечетных частей.
Последовательное двойное преобразованиеГильберта возвращает исходную функцию
с обратным знаком ТН[ТН[x(t)]] = ТН[![]() (t)]
= -x(t). Это определяется тем, что при
двойном преобразовании фазы всех
гармоники сигнала сдвигаются на,
что изменяет знак их гармоник. Однако
в силу исключения из сигнала при первом
преобразовании постоянной составляющей,
при двойном преобразовании сигнал x(t)
восстанавливается с исключенным средним
значением по интервалу задания.
(t)]
= -x(t). Это определяется тем, что при
двойном преобразовании фазы всех
гармоники сигнала сдвигаются на,
что изменяет знак их гармоник. Однако
в силу исключения из сигнала при первом
преобразовании постоянной составляющей,
при двойном преобразовании сигнал x(t)
восстанавливается с исключенным средним
значением по интервалу задания.
Обратное преобразование Гильберта, по существу, это второе преобразование в последовательном двойном преобразовании Гильберта с изменением знака результата:
x(t) = ТH-1[![]() (t)]
= -
(t)]
= -![]() =
=![]() (t)*(-1/t).
(t)*(-1/t).
Альтернативная форма вычисления x(t) из
![]() (t):
(t):
x(t) = TF-1[(j
sgn(f)TF[![]() (t)]].
(t)]].
Подобиепри
изменении масштаба аргумента: ТН[x(at)] =![]() (at).
(at).
Энергетическая эквивалентность:
![]() x2(t) dt =
x2(t) dt =![]()
![]() 2(t)
dt.
2(t)
dt.
Это следует из теоремы Парсеваля
(энергия сигнала равна сумме энергии
всех частотных составляющих сигнала)
и равенства модулей спектров сигналов
x(t) и ![]() (t)
(энергия сигнала не зависит от его
фазовочастотной характеристики).
(t)
(энергия сигнала не зависит от его
фазовочастотной характеристики).
Свойство ортогональности:
![]() x(t)
x(t)![]() (t)
dt = 0
(t)
dt = 0
Если все косинусные составляющие сигнала
x(t) превращаются в ортогональные им
синусные составляющие сигнала ![]() ,
а синусные – в ортогональные им
косинусные, то и сигналы x(t) и
,
а синусные – в ортогональные им
косинусные, то и сигналы x(t) и![]() должны быть ортогональны.
должны быть ортогональны.
Свойство свертки:
TH[x(t) *
y(t)] = ![]() (t)* y(t)
= x(t) *
(t)* y(t)
= x(t) *
![]() (t).
(t).
Это вытекает из следующих соображений. Примем z(t) = x(t)*y(t), при этом:
Z(f) = X(f)Y(f),![]() (f)
= -j sgn(f)Z(f) = -j sgn(f)
X(f)Y(f).
(f)
= -j sgn(f)Z(f) = -j sgn(f)
X(f)Y(f).
![]() (f)
= [-j sgn(f) X(f)]Y(f) =
(f)
= [-j sgn(f) X(f)]Y(f) =![]() (t)Y(f)
(t)Y(f)![]() (t)*y(t).
(t)*y(t).
![]() (f)
= X(f)[-j
sgn(f) Y(f)] = X(f)
(f)
= X(f)[-j
sgn(f) Y(f)] = X(f)![]() (f)
x(t)
*
(f)
x(t)
*![]() (t).
(t).
Отсутствие коммутативностис преобразованием Фурье:
TF[ТН[x(t)]] ТН[TF[x(t)]].
Свойство модуляции: Модулирующие сигналы u(t), как правило, имеют ограниченный спектр, максимальные частоты которогомного меньше значения несущей частотыo, при этом:
ТН[u(t)cos(ot)] = u(t)sin(ot).
Оператор дискретного преобразования Гильбертаhb(kΔt)1/πt на интервале от -Т до Т с шагом Δt можно получить обратным преобразованием Фурье частотной характеристики Hb(f) (выражение 1.3) в интервале от -fNдо fN (fN=1/2Δt). При Δt=1:
hb(kΔt) =![]() Hb(f)
exp(j2πfkΔt) df =
Hb(f)
exp(j2πfkΔt) df =![]() j
exp(j2πfkΔt) df -
j
exp(j2πfkΔt) df -![]() j
exp(j2πfkΔt) df =
j
exp(j2πfkΔt) df =
= [1/(2πkΔt)][1-exp(-jπkΔt)-exp(jπkΔt)+1] = [1/(πkΔt)][1-(exp(-jπkΔt)+exp(jπkΔt)/2] =
= [1/(πkΔt)](1-cos(πkΔt)) = [2/(πkΔt)] sin2(πkΔt/2). (1.4)
hb(kΔt) = 2/(πkΔt),k=1,3,5, ... ,
hb(kΔt) = 0, k = 0,2,4, ... .
Нетрудно убедиться, что коэффициент усиления постоянной составляющей оператора равен нулю.
В частотной области при выполнении преобразования Гильберта спектральных функций оператор свертки hb(kΔf)1/πf не отличается от приведенного для временной области.
Исследование аналогов.
При исследовании устройств, использующих преобразование Гильберта, был найден и исследован патент на “Цифровой измеритель модуляции” (Патент РФ 2248000), измеряющий параметры модулированных сигналов. В этом устройстве преобразование Гильберта находится через прямое и обратное преобразования Фурье, которое затрачивает большее количество ресурсов (в связи с чем его труднее реализовать в бортовых системах). Исследований,аналогичных данной работе,обнаружено не было.
Обзор литературы.
В процессе исследования была рассмотрена различная литературы по радиотехнике и фильтрам. Анализ оптимальности и ошибки предсказания были выполнены с помощью книги “Основы радиоэлектроники и связи, основы оптимального радиоприёма”. Также были изучены различные алгоритмы обработки сигнала в трактах систем пассивной радиолокации (т.е. сигнал имеет доподлинно неизвестные параметры).
В книге “Теоретические основы статистической радиотехники” была рассмотрена структура построения фазового обнаружителя и условие, с помощью которого можно распознать сигнал на фоне шума.
Разработка направлений исследований и выбор оптимального варианта.
Данная работа затрагивает исследование моделей преобразователей Гильберта и нахождение модели, реализующей преобразование Гильберта, наиболее близкое к идеальному. Мною разработаны 2 направления исследований: исследование фильтра Гильберта, сформированного по формуле (1.4) и фильтра, сформированного по методу Паркса-Макклеллана.
В данной работе выбран вариант исследования характеристик фильтра, сформированного по методу Паркса-Макклеллана.
