
3.Метод разделения переменных Фурье
.docМетод разделения переменных Фурье
1. Введение в основные типы уравнений в частных производных II степени.
Многочисленные задачи математической физики, включая задачи механики, теплофизики, электродинамики описываются уравнениями в частных производных II степени. К некоторым, наиболее распространенным основным уравнениями с ч.п. II степени относятся:
а) уравнение
Лапласа
(в трехмерном случае)
![]() или
или
![]() (здесь
(здесь
![]() - неизвестная функция,
- неизвестная функция,
![]() и
т.д. - сокращенные обозначения частных
производных) рассматривается в задаче
со стационарным распределением
температуры или электрического потенциала
внутри пространственной области.
и
т.д. - сокращенные обозначения частных
производных) рассматривается в задаче
со стационарным распределением
температуры или электрического потенциала
внутри пространственной области.
б) волновое
уравнение
![]() (здесь
(здесь
![]() ,
,
![]() - время,
- время,
![]() - параметр) рассматривается в задаче
распространения механических или
электромагнитных колебаний в среде.
- параметр) рассматривается в задаче
распространения механических или
электромагнитных колебаний в среде.
в) уравнение
теплопроводности
![]() рассматривается в задаче распространения
тепла.
рассматривается в задаче распространения
тепла.
Отметим, что данные уравнения также рассматриваются в задачах для двух- и одномерного пространства. Так отдельно выделяется класс линейных уравнений в частных производных II степени относительно функции двух переменных. Общий вид данных уравнений:
![]()
где
![]() - функции независимых переменных
- функции независимых переменных![]() ,
,
![]() - неизвестная функция,
- неизвестная функция,
![]() ,
,
![]() и т.д. – сокращенные обозначения частных
производных.
и т.д. – сокращенные обозначения частных
производных.
Все
уравнения данного класса, в зависимости
от знака дискриминанта
![]() можно разделить на три основных типа:
можно разделить на три основных типа:
а) уравнения
эллиптического
типа (![]() )
– описывают стационарные процессы,
т.е. процессы не изменяющиеся по времени,
пример
)
– описывают стационарные процессы,
т.е. процессы не изменяющиеся по времени,
пример
![]() - уравнение Лапласа для двумерной
поверхности (мембрана, круг и т.д.)
- уравнение Лапласа для двумерной
поверхности (мембрана, круг и т.д.)
б) уравнения
гиперболического
типа (![]() )
– описывают процессы распространения
волн, пример
)
– описывают процессы распространения
волн, пример
![]() - волновое уравнение в задаче колебания
струны.
- волновое уравнение в задаче колебания
струны.
в)
уравнения параболического
типа
(![]() )
– описывают процессы распространения
тепла, пример
)
– описывают процессы распространения
тепла, пример
![]() - уравнение теплопроводности в задаче
нагрева/охлаждения стержня.
- уравнение теплопроводности в задаче
нагрева/охлаждения стержня.
Понятие задачи
Общее решение уравнения в частных производных представляет собой бесконечное множество функций от независимых переменных. Для того чтобы выделить единственное решение необходимо задать дополнительные условия – временные и/или краевые. Тем самым вводится понятие задача – это уравнения с дополнительными условиями. Примерами задач являются:
а) задачи распространения волн и тепла в бесконечном стержне:

![]()
![]()

![]()
![]()
здесь
указано, что пространственная координата
не имеет ограничений (нет краевых
условий), но вводится начальное условие:
при
![]() функция
функция
![]() имеет заданный вид
имеет заданный вид
![]() (для гиперболического уравнения –
дополнительное условие на скорость
функции -
(для гиперболического уравнения –
дополнительное условие на скорость
функции -
![]() в начальный момент). Данного типа задачи
с начальными условиями именуются
задачами Коши.
в начальный момент). Данного типа задачи
с начальными условиями именуются
задачами Коши.
Если вышеуказанные процессы рассматривать в ограниченной области пространства, то начальные условия дополняются граничными, тем самым рассматриваются смешанные задачи:
б) задача колебания закрепленной на концах струны:


![]()
здесь
область пространства ограниченна
![]() ,
кроме начального заданы также краевые
условия (т.к. струна закреплена, то ее
колебания
,
кроме начального заданы также краевые
условия (т.к. струна закреплена, то ее
колебания
![]() в точках
в точках
![]() и
и
![]() в любой момент времени отсутствуют)
в любой момент времени отсутствуют)
в) задача нагрева/охлаждения стержня:


![]()
Отметим,
что возможны и другие виды граничных
условий (в частности производные от
функции
![]() на концах стержня и т.д.)
на концах стержня и т.д.)
Для эллиптических задач (при рассмотрении стационарных явлений) вводятся краевые (граничные) условия, среди которых выделяют три основных:
а) граничное
условие I
рода (условие Дирихле) - решение
эллиптического уравнения ищется в
некоторой области пространства
![]() при заданном значении на границе этой
области
при заданном значении на границе этой
области
![]() ,
например для уравнения Лапласа:
,
например для уравнения Лапласа:
![]()
![]()
 Пример
задачи Дирихле для уравнения Лапласа
– распространение температуры/эл.
заряда внутри некоторого тела при
заданной температуре/потенциале на его
поверхности.
Пример
задачи Дирихле для уравнения Лапласа
– распространение температуры/эл.
заряда внутри некоторого тела при
заданной температуре/потенциале на его
поверхности.
б) граничное
условие II
рода (условие Неймана) - решение
эллиптического уравнения ищется в
некоторой области пространства
![]() при заданном значении на границе этой
области
при заданном значении на границе этой
области
![]() внешней нормальной производной искомой
функции -
внешней нормальной производной искомой
функции -
![]() :
:

![]()
Пример задачи Неймана для уравнения Лапласа – распространение температуры/эл. заряда внутри некоторого тела при заданном потоке температуры/заряде на его поверхности.



![]()
![]()




в) граничное
условие III
рода (условие Робэна) - решение
эллиптического уравнения ищется в
некоторой области пространства
![]() ,
удовлетворяющее на границе этой области
,
удовлетворяющее на границе этой области
![]() условию
условию
![]() ,
где
,
где
![]() - некоторые функции:
- некоторые функции:

![]()
Отметим,
что для различных уравнений, описанных
в эллиптических задачах, необходимо
выполнение дополнительных условий,
связанных с физической сутью задач. Так
для уравнения Лапласа в задаче Неймана
накладывается ограничение:
![]() - т.е. полный поток через всю поверхность
тела должен равняться нулю (входящий
поток равен исходящему).
- т.е. полный поток через всю поверхность
тела должен равняться нулю (входящий
поток равен исходящему).
2. Метод Фурье
О дним
из наиболее изученных методов решений
частных производных II
порядка является метод разделения
переменных (метод Фурье). Для рассмотрения
данного метода воспользуемся следующим
примером: дана задача о распределении
заряда на прямоугольной пластине в
случае, если на левую сторону нанесен
потенциал (переменный вдоль стороны)
дним
из наиболее изученных методов решений
частных производных II
порядка является метод разделения
переменных (метод Фурье). Для рассмотрения
данного метода воспользуемся следующим
примером: дана задача о распределении
заряда на прямоугольной пластине в
случае, если на левую сторону нанесен
потенциал (переменный вдоль стороны)
Данная задача представляет собой задачу Дирихле для эллиптического уравнения Лапласа на плоскости:


В
методе Фурье решение ищется в виде
функции с разделенными переменными, в
данном случае
![]() .
При подстановке данной функции в исходное
уравнение все частные производные
обратятся в обыкновенные:
.
При подстановке данной функции в исходное
уравнение все частные производные
обратятся в обыкновенные:
![]()
![]()
При этом само уравнение обратится в уравнение с разделенными переменными (в дальнейшем будем опускать обозначения переменных функций):
![]()
Непосредственно разделяя переменные, получим:
![]()
Так как правая и левая части уравнений зависят от разных переменных, то они равны только в том случае, если являются константой, т.е.
![]()
Отсюда можно записать систему из двух обыкновенных дифференциальных уравнений:
(1) ![]()
Далее рассматривают решение одного из этих уравнений, учитывая заданные граничные условия. В данном случае возьмем второе уравнение, для которого граничные условия выводятся следующим образом:
![]() для
нетривиальных значений
для
нетривиальных значений
![]()
Аналогично:
![]() -
т.е. оба граничных условия для данного
уравнения однородны.
-
т.е. оба граничных условия для данного
уравнения однородны.
В итоге получаем обыкновенное однородное дифференциальное уравнение с однородными граничными условиями:
![]()
Решение
данной системы представляет собой
задачу
Штурма-Лиувилля.
Эта задача связанна с поиском собственных
значений (чисел) константы
![]() и связанных с ними собственными функциями
и связанных с ними собственными функциями
![]() ,
при этом доказано, что существует счетное
(дискретное) множество этих функций
(чисел).
,
при этом доказано, что существует счетное
(дискретное) множество этих функций
(чисел).
Задача Штурма-Лиувилля
Рассмотрим однородное дифференциальное уравнение системы. Для нахождения его общего решения необходимо составить характеристическое уравнение и найти его корни:
![]()
В
зависимости от знака константы, структура
общего решения будет различаться. При
этом для нахождения частных решений
необходимо использовать краевые условий
![]() .
Возможны три ситуации:
.
Возможны три ситуации:
а) ![]()
-
общее решение:

-
частное решение:
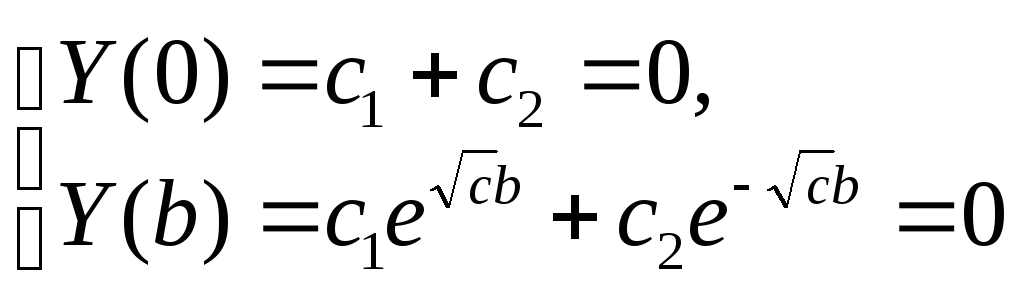 ,
можно показать, что данная система
имеет нетривиальное решение только в
случае, если
,
можно показать, что данная система
имеет нетривиальное решение только в
случае, если
 ,
что противоречит условию данной
структуры общего решения.
,
что противоречит условию данной
структуры общего решения.
б) ![]()
-
общее решение:

-
частное решение:
 и данная система не имеет нетривиальных
решений.
и данная система не имеет нетривиальных
решений.
в) ![]()
-
общее решение: т.к.
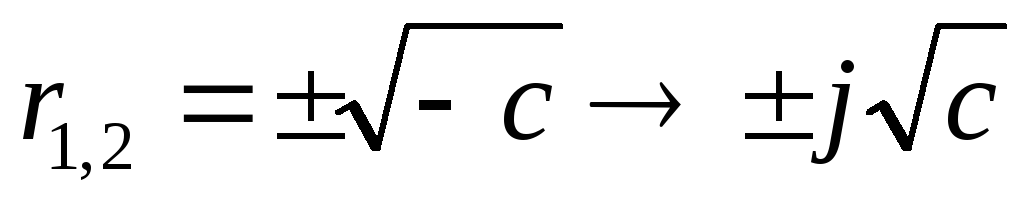 ,
то
,
то

-
частное решение:


Последнее уравнение обладает бесконечным множеством нетривиальных решений:
![]() где
где
![]()
Отсюда
искомая функция
![]() запишется в виде:
запишется в виде:
![]()
Непосредственной
подстановкой в исходное уравнение можно
доказать что данная функция является
частным решением для любых значений
![]() .
Для счетного множества значений
.
Для счетного множества значений
![]() ,
множества собственных чисел и функций
запишутся в виде:
,
множества собственных чисел и функций
запишутся в виде:
(2) ![]() ,
,
![]()
Метод Фурье (продолжение)
Рассмотрим первое уравнение системы (1):
![]()
Его
общее решение с учетом корней
характеристического уравнения (![]() )
и положительности значений константы
(
)
и положительности значений константы
(![]() )
запишется в виде:
)
запишется в виде:
![]() (здесь
(здесь
![]() –
константы интегрирования)
–
константы интегрирования)
Для
дальнейших построений, воспользуемся
одним из граничных условий уравнения
(1), а именно однородным условием:
![]() .
Подставляя в него полученное выше
решение, получим:
.
Подставляя в него полученное выше
решение, получим:
![]()
Т.е.
формула для
![]() запишется следующим образом:
запишется следующим образом:
![]() .
Данное выражение обычно записывают в
более удобном виде, приводя к формуле
для гиперболического синуса:
.
Данное выражение обычно записывают в
более удобном виде, приводя к формуле
для гиперболического синуса:
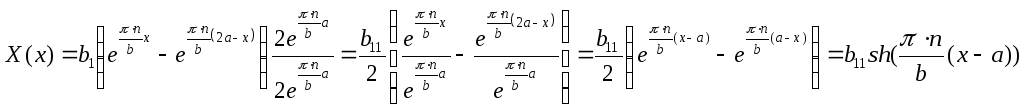
Множество собственных функций в данном случае:
![]()
Теперь
можно обратиться к общей идеи метода
Фурье – к поиску всего многообразия
частных решений в виде
![]() .
Доказано, что линейная комбинация
частных решений также является частным
решением, поэтому наиболее «полное»
решение исходной задачи представляется
следующей зависимостью:
.
Доказано, что линейная комбинация
частных решений также является частным
решением, поэтому наиболее «полное»
решение исходной задачи представляется
следующей зависимостью:
![]()
где
![]() - константы, значение которых необходимо
определить, используя условия задачи.
- константы, значение которых необходимо
определить, используя условия задачи.
В
нашем случае однородные граничные
условия для
![]() и
и
![]() использовались для решения задачи
Штурма – Лиувилля, поэтому для определения
использовались для решения задачи
Штурма – Лиувилля, поэтому для определения
![]() используем неоднородное граничное
условие:
используем неоднородное граничное
условие:
![]() .
Имеем:
.
Имеем:
![]()
(при
этом можно показать, что
![]() ).
Подставляя данное выражение в граничное
условие
).
Подставляя данное выражение в граничное
условие
![]() ,
получим:
,
получим:
![]()
Учитывая
выражения для коэффициентов Фурье для
тригонометрического ряда (для нечетных
функций:
![]() ),
запишем:
),
запишем:
![]()

Тем самым мы получили искомый ответ исходной задачи:
![]() ,
,
где

Для
проверки этого решения его необходимо
подставить в исходное уравнение, что с
учетом наличия рядов является трудоемкой
задачей. Для упрощения процедуры,
преобразуем исходную задачу, а именно
выберем конкретный вид функции
![]() :
:
![]() .
.
Находя
коэффициенты
![]() ,
получим:
,
получим:

для
![]()

для
![]()

Окончательный
результат:
 можно проверить непосредственно
подстановкой в исходное уравнение.
можно проверить непосредственно
подстановкой в исходное уравнение.
Представленный
вывод может быть получен более простым
способом - непосредственной анализом
«общей» линейной последовательности
![]() по известному (конкретному) граничному
условию
по известному (конкретному) граничному
условию
![]() .
.
Имеем:
![]() .
Для любых
.
Для любых
![]() нет значений
нет значений
![]() приводящих данное выражение в верное
тождество. Соответственно для
приводящих данное выражение в верное
тождество. Соответственно для
![]() получаем:
получаем:

Задания
Для рассмотренного в методичке примера решить следующие задачи





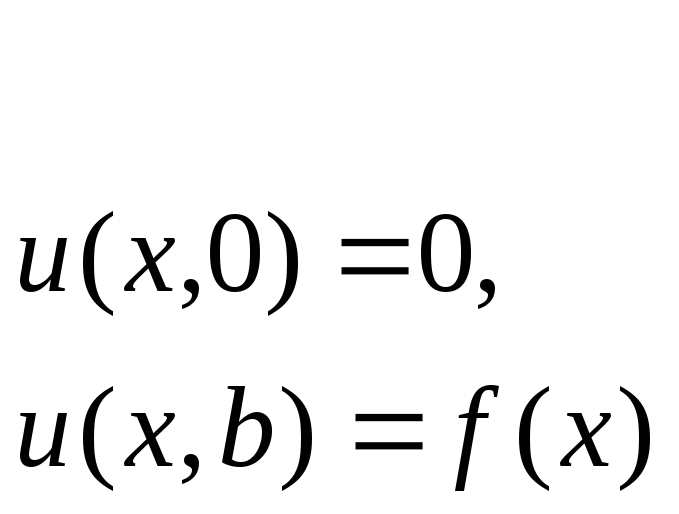
Проверить
решения на примерах с заданными функциями
неоднородных граничных условий (как в
приведенном ранее примере, где
![]() ).
).
