
1.4 Уравнение равносторонней гиперболы
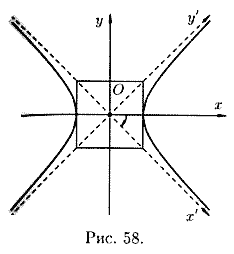
Гипербола (11.9) называется равносторонней, если ее полуоси равны (a=b). Ее каноническое уравнение
![]() (11.12)
(11.12)
Асимптоты равносторонней гиперболы имеют уравнения y=x и y= - x и, следовательно, являются биссектрисами координатных углов.
Рассмотрим уравнение этой гиперболы в новой системе координат Ox’y’ (см. рис. 58), полученной из старой поворотом осей координат на угол a= - Pi/4. Используем формулы поворота осей координат :
![]()
Подставляем значения х и у в уравнение (11.12):
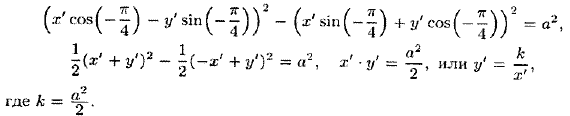
Уравнение равносторонней гиперболы, для которой оси Ох и Оу являются асимптотами, будет иметь вид y=k/x.
1.5 Дополнительные сведения о гиперболе
Эксцентриситетом гиперболы (11.9) называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается ε:

Так
как для гиперболы с>a,
то эксцентриситет гиперболы больше
единицы: ε>1. Эксцентриситет характеризует
форму гиперболы. Действительно, из
равенства (11.10) следует,
что b^2/a^2=(c^2/a^2)-1 т.е. b/a=
(ε^2-1)^1/2 и 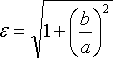 .
.
Отсюда видно, что чем меньше эксцентриситет гиперболы, тем меньше отношение — ее полуосей, а значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет равносторонней гиперболы равен 2^1/2. Действительно,
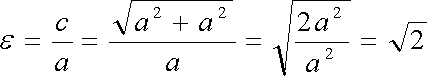
Фокальные
радиусы ![]() и
и ![]() для
точек правой ветви гиперболы имеют
вид r1=
εx+a и r2=
εx
- a,
а для левой — r1=
-(εx+a) и
r2=
- (εx-a).
для
точек правой ветви гиперболы имеют
вид r1=
εx+a и r2=
εx
- a,
а для левой — r1=
-(εx+a) и
r2=
- (εx-a).
Прямые x=+-a/ ε — называются директрисами гиперболы. Так как для гиперболы ε > 1, то a/ ε<a. Это значит, что правая директриса расположена между центром и правой вершиной гиперболы, левая — между центром и левой вершиной.
Директрисы гиперболы имеют то же свойство r/d= ε, что и директрисы эллипса.
Кривая, определяемая уравнением y^2/b^2-x^2/a^2=1 также есть гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2a — на оси Ох. На рисунке 59 она изображена пунктиром.
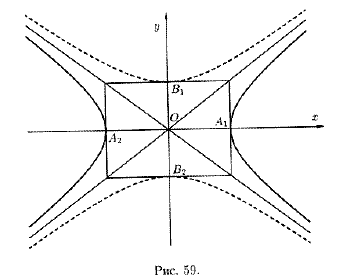
Очевидно, что гиперболы x^2/a^2-y^2/b^2=1 и y^2/b^2-x^2/a^2=1 имеют общие асимптоты. Такие гиперболы называются сопряженными.
Пример 1
Составить простейшее уравнение гиперболы, если расстояние между ее вершинами равно 20, а расстояние между фокусами 30.
Решение.
Вершины параболы лежат на ее действительной оси. По условию 2a = 20; 2c = 30. Значит, a = 10; c = 15; a2 = 100; c2 = 225.
Величины a, b, c у гиперболы связаны соотношением
a2 + b2 = c2;
отсюда b2 = c2 - a2 = 225 - 100; b2 = 125.
Значит, уравнением гиперболы будет
![]()
![]()
Пример 2
Уравнения асимптот гиперболы y = x/2 и y = -x/2, а расстояние между фокусами 2c = 10. Найти уравнение гиперболы.
Решение.
Уравнения асимптот гиперболы имеют вид
![]()
![]()
Из
условия задачи следует, что: 1) ![]()
![]() и a =
2b;
2) c =
5. Подставляя в соотношение a2 + b2 = c2 значения
a =
2b и c =
5, получим (2b)2 + b2 =
25; b2 =
5; a =
2b,
а потому a2 =
4b2 =
20.
и a =
2b;
2) c =
5. Подставляя в соотношение a2 + b2 = c2 значения
a =
2b и c =
5, получим (2b)2 + b2 =
25; b2 =
5; a =
2b,
а потому a2 =
4b2 =
20.
Искомым
уравнением гиперболы будет ![]()
![]()
![]() .
.
Заключение
Вряд ли можно найти лучше пример, чем исследования древними греками кривых второго порядка. Вплоть до XVII века их исследования не имели практического приложения, но именно к этому времени был изобретен метод координат. Именно переводя геометрические понятия на язык координат, мы получаем возможность рассматривать алгебраические. Наглядный пример – задача об окружности Аполлония: “Найти геометрическое место точек М, отношение расстояний которых до данных точек А и В, постоянно”. Ее геометрическое решение помещено в трактате “О кругах” (II век до н.э.) и оно довольно сложно, а если ее перевести на язык координат, решение совсем доступно.
Интерес к коническим сечениям особенно возрос после того, как Галилей установил, что тело, брошенное под углом к горизонту, двигается по параболе, и Кеплер сформулировал законы движения планет, согласно которым они описывают эллипсы.
Изучение кривых второго порядка дало толчок развитию теорий алгебраических и механических кривых: лемнискаты, конхоиды, циклоиды, эпициклоиды, гипоциклоиды, кардиоиды и т.д. Изучение этих кривых, их свойств могут вылиться в интересные ученические исследовательские работы.
Сonclusion
It is unlikely it is possible to find better an example, than researches by ancient Greeks of curves of the second order. Up to the XVII century of their research had no practical application, but the method of coordinates was invented exactly by this time. Exactly translating geometrical concepts into language of coordinates, we have an opportunity to consider the algebraic. A bright example – a task about a circle Apollonia: "To find the M locus, which relation of distances to these points And and In, it is constant". Its geometrical decision is placed in the treatise "About Circles" (the II century BC) and it is quite difficult and if it to translate to language of coordinates, the decision is absolutely available.
Interest in conic sections especially increased after Galilei established that the body thrown at an angle to the horizon moves on a parabola, and Kepler formulated laws of the movement of planets according to which they describe ellipses.
Studying of curves of the second order gave an impetus to development of theories of algebraic and mechanical curves: lemniskata, conchoids, cycloid, epicycloids, hypocycloid, cardioids, etc. Studying of these curves, their properties can develop into interesting student's research works.
Литература
Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64—69.
Александров П. С., Лекции по аналитической геометрии, М. - 1968.
Васильев Н.Б., Гутенмахер В.Л. Прямые и кривые. Изд-во “Наука”, М. – 1970.
Интернет ресурс // pm298.ru
Интернет ресурс // znannya.org
Интернет ресурс //math.semestr.ru
