
Оглавление
Введение
Линия (кривая) второго порядка - С.4-5.
Гипербола. Каноническое уравнение гиперболы - С.6.
Исследование формы гиперболы по её уравнению – С.7-8.
Асимптоты гиперболы – С. 9-10.
Уравнение равносторонней гиперболы – С.11-12.
Дополнительные сведения о гиперболе – С.13-14.
Пример 1 – С.15.
Пример 2 – С.16.
Заключение
Литература
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Introduction
For the first time we studied the curves of the second order one of the disciples of Plato. His work was as follows: if you take the two intersecting lines and rotate them around the bisector of the angle formed by them, you get a cone surface. If surface cross this plane in the cross section is different geometric shapes, namely an ellipse, circle, parabola, hyperbola and more degenerate shapes.
However, the application of scientific knowledge found only in the XVII, when it became known that the planets move in elliptical paths, and a cannon projectile flies in a parabolic. Still later it became known that give the body if the first cosmic velocity, it will move in a circle around the Earth, increasing this rate - an ellipse, and on reaching escape velocity the body of a parabola leave Earth's gravity field.
1. Линия (кривая) второго порядка
Линией (кривой) второго порядка называется линия, общее уравнение которой имеет следующий вид:
![]() .
.
Уравнение
второй степени вида
![]() (не
содержащее члена
(не
содержащее члена ![]() c произведением координат) называется
пятичленным уравнением кривой второго
порядка. Оно определяет на плоскости
c произведением координат) называется
пятичленным уравнением кривой второго
порядка. Оно определяет на плоскости![]() эллипс,
гиперболу и параболу (с возможными
случаями распада и вырождения этих
кривых) с осями симметрии, параллельными
осям координат, в зависимости от знака
произведения коэффициентов
эллипс,
гиперболу и параболу (с возможными
случаями распада и вырождения этих
кривых) с осями симметрии, параллельными
осям координат, в зависимости от знака
произведения коэффициентов![]() и
и![]() .
.
Центром некоторой линии называется такая точка плоскости, по отношению к которой точки этой линии расположены симметрично парами. Линии второго порядка, обладающие единственным центром, называются центральными. Координаты центра S(x0 ; y0) линии определяются из системы:
![]()
Обозначим
через ![]() .
.
При Δ≠0 кривая второго порядка будет центральной. Причем, при Δ>0 уравнение является уравнением эллиптического типа. Каждое эллиптическое уравнение является уравнением либо обыкновенного эллипса, либо вырожденного эллипса (точка), либо мнимого эллипса (в этом случае уравнение не определяет на плоскости никакого геометрического образа). При Δ<0 уравнение является уравнением гиперболического типа. Каждое гиперболическое уравнение определяет либо обыкновенную гиперболу, либо вырожденную (пару пересекающихся прямых). При Δ=0 линия второго порядка не является центральной. Такие уравнения называются уравнениями параболического типа и определяют на плоскости либо обыкновенную параболу, либо пару параллельных (или совпадающих) прямых, либо не определяют на плоскости никакого геометрического образа.
1.1 Гипербола. Каноническое уравнение гиперболы
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
 Обозначим
фокусы через F1 и F2 расстояние
между ними через 2с,
а модуль разности расстояний от
каждой точки гиперболы до фокусов
через 2a.
По определению 2a < 2с,
т. е. a < c.
Обозначим
фокусы через F1 и F2 расстояние
между ними через 2с,
а модуль разности расстояний от
каждой точки гиперболы до фокусов
через 2a.
По определению 2a < 2с,
т. е. a < c.
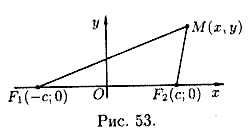
Для вывода уравнения гиперболы выберем систему координат Oxy так, чтобы фокусы F1 и F2 лежали на оси Ox, а начало координат совпало с серединой отрезка F1F2 (см. рис. 53). Тогда фокусы будут иметь координаты F1(c;0) и F2(-c;0)
Пусть M(x;y) —
произвольная точка гиперболы. Тогда
согласно определению гиперболы
|MF1-MF2|=2a
или
MF1-MF2=+-2a,
т.е.![]() .
После упрощений, как это было сделано
при выводе уравнения эллипса, получимканоническое
уравнение гиперболы
.
После упрощений, как это было сделано
при выводе уравнения эллипса, получимканоническое
уравнение гиперболы
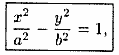 (11.9)
(11.9)
![]() (11.10)
(11.10)
Гипербола есть линия второго порядка.
