Nachertatelnaya_geometriya_ch2_Kirillov_Haydarov_sredn._prof.obuch_2013

Минобрнауки России

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный технологический институт (технический университет)»

Кафедра инженерного проектирования

Д.Л. Кириллов, В.А. Люторович, Г.Г. Хайдаров, И.Н. Низовцева

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.

ЧАСТЬ ВТОРАЯ

Учебное пособие

Санкт-Петербург

2013

УДК 331.875

Кириллов, Д.Л. Начертательная геометрия. Часть вторая : учебное пособие / Д.Л. Кириллов, В.А. Люторович, Г.Г. Хайдаров, И.Н. Низовцева – СПб.:

СПбГТИ(ТУ), 2013. – 46 с.

Во второй части изложены основные теоретические вопросы начертательной геометрии по темам: «Плоскость» и «Прямая и плоскость».

Авторы учитывали, что читатель может интересоваться не обязательно всеми вопросами. В соответствии с этим пособие построено так, что отдельные разделы могут изучаться сравнительно независимо друг от друга.

Учебное пособие формирует у студентов следующие профессиональные компетенции:

а) общекультурные (ОК):

- способность к приобретению с большой степенью самостоятельности новых знаний с использованием современных образовательных и инновационных технологий (ОК-7);

б) профессиональные (ПК):

-участие в подготовке технической документации на машины, приводы, различные комплексы и технологические процессы на производственных участках;

-участие в подготовке технической документации на ремонт оборудования

-владение основными законами построения изображений и нанесение размеров на рабочих чертежах деталей (ПК-3);

Учебное пособие предназначено для студентов Центра среднего профессионального образования при СПб ГТИ(ТУ), обучающихся по специальности 240134 «Переработка нефти и газа».

Рис. 36, библиогр. назв. 9

Рецензенты: 1 СПбГЭУ «ЛЭТИ» им. В.И. Ульянова (Ленина), доцент кафедры прикладной механики и инженерной графики В.П.Большаков 2 А.Ю. Иваненко, канд. техн. наук, доцент кафедры

оптимизации химической и биотехнологической аппаратуры СПбТИ(ТУ)

Утверждено на заседании учебно-методической комиссии механического факультета 14 мая 2013 г.

Рекомендовано к изданию РИСо СПбГТИ (ТУ)

ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ

Обозначения геометрических фигур

1 Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита А, В, С, D…или арабскими цифрами 1, 2,

3, 4…

2 Последовательность точек (и других элементов) – надстрочными

индексами: АI, ВI, СI…

3 Линии в пространстве – по точкам, определяющим линию или строчными буквами латинского алфавита: a, b, c…

4Углы – строчными буквами греческого алфавита μ, ρ, σ, φ, ω.

5Плоскости – строчными буквами греческого алфавита α, β, γ, σ, ε.

6Поверхности – римскими цифрами I, II, III, IV а также прописными буквами русского алфавита: цилиндр – Ц, конус – К, сфера – Сф…

7Плоскости проекций – строчной буквой греческого алфавита π. Произвольная плоскость – π0, горизонтальная – π1, фронтальная – π2, профильная – π3, любая дополнительная – π4, π5…

8Оси проекций – строчными буквами х, у, z или (при введении дополнительных плоскостей) π2/π1, π2/π3, π2/π5…Начало координат – пропис-

ной буквой О.

9Проекции точек:

-на горизонтальную плоскость π1 – АI, ВI, СI…

-на фронтальную плоскость π2 – АII, ВII, СII…

-на профильную плоскость π3 – АIII, ВIII, СIII…

-на дополнительную плоскость π4 – АIV, ВIV, СIV…

10Проекции линий – по проекциям точек, определяющих линию; кроме того:

-горизонтальная линия (первая параллель) – буквой h;

-фронтальная линия (вторая параллель) – буквой f;

-профильная линия (третья параллель) – буквой р.

11Обозначение плоскостей, заданных следами:

-горизонтальный след плоскости α – hIоα

фронтальный след плоскости α - fIIоα профильный след плоскости α – рIIIоα

В тех случаях, когда плоскость не требует наименования, обозначение следов упрощённо – hIо, fIIо, рIIIо

3

Для проецирующих плоскостей задаётся проекция плоскости: αI – горизонтально - проецирующая плоскость

αII – фронтально – проецирующая плоскость

αIII – профильно – проецирующая плоскость

12 Точки схода следов плоскости – прописными буквами X, Y, Z с индексом соответствующей плоскости: Xα, Yα, Zα.

Обозначения отношений между геометрическими элементами

1 Совпадение ( ≡ ):

А ≡ В – точки А и В совпадают. 2 Параллельность ( ║ ):

a║b - прямые a и b параллельны.

3 Перпендикулярность ( ┴ ):

a ┴ α - Прямая a перпендикулярна плоскости α.

Обозначения теоретико – множественные

1 Принадлежность ( ):

А а – точка А принадлежит прямой а. 2 Включение ( ):

A α – прямая α принадлежит плоскости α.

3Пересечение ( ):

А= а α – точка А есть пересечение прямой а с плоскостью α.

4Импликация – логическое следствие ( ):

а║с, b║c a║b – если а и b параллельны прямой с, то они параллельны между собой.

4

Данное издание является продолжением учебного пособия Кириллов, Д.Л. Начертательная геометрия. Часть первая : учебное пособие / Д.Л. Кириллов, В.А. Люторович, Г.Г. Хайдаров, И.Н. Низовцева – СПб.:

СПбГТИ(ТУ), 2013. – 37с.

4 ПЛОСКОСТЬ

Плоскостью называется поверхность, обладающая тем свойством, что прямая, проходящая через любые две точки этой поверхности, лежит в ней всеми остальными точками.

Задание плоскости на чертежах осуществляется заданием геометрических элементов, определяющих положение этой плоскости в пространстве.

4.1 Способы задания плоскости

Различают следующие способы задания плоскости:

-задание равнозначными геометрическими элементами;

-задание следами этой плоскости;

-задание плоскими фигурами.

Рассмотрим подробнее каждый из этих способов.

К первому способу относят задание плоскости изображениями (Рисунок 4.1):

а - трёх точек, не лежащих на одной прямой; б - прямой и точки вне этой прямой; в - двух пересекающихся прямых; г - двух параллельных прямых.

Рисунок 4.1– Равнозначные геометрические элементы

Следом плоскости на данной плоскости координат называется линия пересечения плоскости с указанной плоскостью координат. Зада-

ние плоскости следами обеспечивает наглядность изображения и позволяет наиболее просто решать задачи, связанные с построением изображений геометрических элементов, расположенных в этой плоскости.

5

Плоскостью общего положения называют плоскость, пересекающую все оси координат.

Покажем на чертеже (Рис.4.2, а) изображения осей координат и отме-

тим на них произвольные точки Xα, Yα, Zα.

а б а – аксонометрическое изображение на плоскости эпюра; б – прямоугольное изображение

Рисунок 4.2 – Следы плоскости

Соединяя эти точки прямыми линиями, получим изображение плоскости в виде треугольника, называемого треугольником следов. Сторонами этого треугольника являются линии пересечения плоскости общего положения α с плоскостями координат – следы плоскости.

Их называют: горизонтальным следом hIоα, фронтальным следом fIIоα, профильным следом pIIIоα плоскости α.

Точки Xα, Yα, Zα называют точками схода следов. Положение плос-

OZα=Z).

Три заданных по величине и знаку параметра плоскости определяют положение её в системе координат.

Изображение следов плоскости в прямоугольных проекциях получают, откладывая на соответствующих осях координат (см. Рисунок 2, б) значе-

ния параметров плоскости. Соединяя точки схода следов Xα, Yα, Zα прямыми линиями, получают изображения следов плоскости. Отметим, что

6

отрезок OYα откладывается дважды – на горизонтальной и вертикальной составля-ющих оси Oу.

Для задания положения плоскости достаточно показать на чертеже два следа этой плоскости, так как при этом задаются все три параметра плоскости.

Рассмотрим пример построения следов плоскости общего положения с одним отрицательным параметром.

Пусть задана плоскость (X, Y, -Z). Откладывая на изображениях осей координат (Рисунок 4.3, а) значения параметров (с учётом коэффициентов искажения по осям), получим изображения точек схода следов Xα, Yα и

Zα.

а – аксонометрическое изображение на плоскости эпюра; б – прямоугольное изображение

Рисунок 4.3 – Построение следов плоскости

Соединив попарно эти точки прямыми линиями, получим изображения

следов fIIоα, hIоα, pIIIоα. При этом, как правило, показывают сплошными линиями только те части следов, которые располагаются на плоскостях координат, ограничивающих первый октант.

Для построения прямоугольных проекций следов плоскости нанесём на чертёж (см. Рисунок 4.3, б) оси координат. Откладывая заданные значения

параметров, отмечаем точки схода следов Xα, Yα и Zα. Соединяя эти точки попарно прямыми линиями, получаем изображения следов.

7

Любую плоскую фигуру можно представить как часть плоскости, ограниченную ломаной или кривой линиями. Следовательно, задавая положения плоской фигуры в пространстве, тем самым мы задаём положение плоскости, частью которой является эта фигура. Положение плоской фигуры в пространстве определяется двумя её проекциями на плоскости координат. Так, чтобы построить проекции плоского многоугольника, достаточно построить проекции его вершин.

Треугольник, параллелограмм и трапеция, расположенные в плоскости общего положения, проецируются на плоскости координат соответственно в виде треугольника, параллелограмма и трапеции.

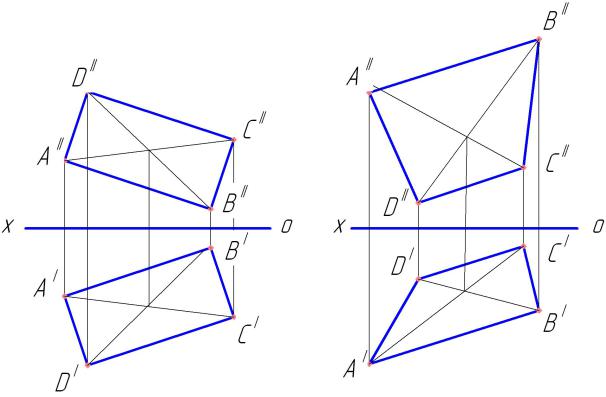
Это обусловлено тем, что три вершины треугольника как три любые точки, не лежащие на одной прямой, всегда лежат в одной плоскости. Покажем на чертеже (Рис.4.4, а) произвольную горизонтальную проекцию параллелограмма (AIBI||CIDI, AIDI||BICI).

а – трапеция; б – параллелограмм Рисунок 4.4 – Плоские фигуры

Фронтальную его проекцию найдём, построив вертикальные проекции вершин и выдерживая лишь проекционные связи между точками и параллельность между проекциями соответствующих сторон (AIIBII||CIIDII, AIIDII||BIICII). Построение проекций трапеции (Рис.4.4, б) аналогично построению проекций параллелограмма. При этом должна быть выдержана

8

лишь параллельность двух её сторон, например: AIBI||CIDI,

AIIBII||CIIDII.

4.2 Прямая и точка в плоскости

Известно, что прямая лежит в плоскости, если две точки прямой лежат в этой плоскости. Чтобы построить прямую, лежащую в заданной плоскости, достаточно соединить прямой линией две точки, заведомо лежащие в плоскости. Такими точками могут быть и точки, расположенные на следах плоскости.

Пусть дана плоскость общего положения α (Рисунок 4.5, а). Требуется построить прямую, лежащую в этой плоскости. Отметим на изображениях следов hIоα и fIIоα две произвольные точки, соответственно, M и N. Соединяя прямой точки M и N, получим изображение отрезка, лежащего в плоскости α. Точки M и N принадлежат следам hIоα и fIIоα и расположены, соответственно, в плоскостях координат π1 и π2. Следовательно, для построенной прямой точки M и N являются следами.

а б а – аксонометрическое изображение на плоскости эпюра; б – прямоугольное изображение

Рисунок 4.5 – Прямая MN и точка 1 в плоскости α

Из изложенного следует, что прямая лежит в плоскости, если её следы лежат на соответствующих следах плоскости.

9

Построим горизонтальную и фронтальную проекции прямой MN (Рисунок 4.5, а). При этом горизонтальная проекция MI горизонтального сле-да и фронтальная проекция NII фронтального следа совпадут с изображениями точек M и N. Фронтальную проекцию MII горизонтального следа и горизонтальную проекцию NI фронтального следа получим, по-

строив изображение перпендикуляров, опущенных из точек M и N на ось

ох (MIMII||оуи

NIINI||оz). Соединяя прямыми линиями соответствующие проекции следов, найдём изображения проекций прямой MN.

Чтобы построить прямоугольные проекции прямой общего положения, лежащей в плоскости, заданной следами (см. Рисунок 4.5, б), отмечают на следах плоскости две точки, например MI и NII. Принимая эти точки, соответственно, за горизонтальную проекцию горизонтального следа и фронтальную проекцию фронтального следа искомой прямой, строят проекции MII и NI, опуская перпендикуляры из точек MI и NII на ось ох. Соединяя соответствующие проекции следов прямыми линиями, получают проекции прямой, лежащей в плоскости α.

Чтобы построить точку, лежащую в плоскости, нужно провести вспомогательную прямую, лежащую в плоскости, и на не взять точку.

Например, точка 1 (1I,1II), взятая на прямой MN (Рисунок 4.5, б), лежит в плоскости α.

Рассмотрим частные случаи положения прямой в плоскости общего положения. К таким случаям относят прямые, лежащие в данной плоскости и параллельные какой – либо плоскости координат (линии уровня).

Прямая, лежащая в плоскости и параллельная плоскости π1 называется горизонталью плоскости. Горизонталь параллельна горизонтальному следу плоскости.

Построим проекции горизонтали плоскости общего положения (Рисунок 4.6, а, б).

10