Зачет матан 1 семестр
.pdf
1) Векторы . Операции над векторами и их свойства
Векторная величина – величина, характеризующаяся числовым значением и направлением.
Геометрический вектор направленный отрезок.
Нулевой вектор вектор, начало и конец которого совпадают (модуль равен нулю)
Модуль вектора – длина вектора – длина направленного отрезка, представляющего его.
Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными.
Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.
Направленные отрезки эквивалентны, если выполнены условия: AB││CD
│AB│=│CD│
↑↑
Векторы – класс эквивалентных друг другу направленных отрезков. Операции над векторами:
1.Сложение векторов
правило треугольника
правило параллелограмма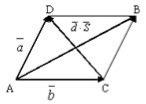
правило многоугольника
|
|
|
|
|
|
2. Под разностью векторов |
и понимаютвектор d = |
|
– |
||
a |
|||||
b такой, что d +b = a
В параллелограмме – это другая диагональ 3. Умножение вектора на число
2. Определение линейной зависимости векторов
Если линейная комбинация |
может |
представлять собой нулевой вектор тогда, когда средичисел
есть хотя бы одно, отличноеотнуля, тосистемавекторов называется линейно зависимой.
3) Определение линейной независимости векторов
Если линейная комбинация 
представляет собой нулевой вектор только тогда, когда все числа 
равны
нулю, то система векторов |
называется линейно |
независимой. |
|
4) Теоремы о линейной независимости векторов
Th о линейной зависимости векторов.
А)Если среди векторов а1,а2,...,аn найдется 1 нулевой вектор, то вся система векторов линейно зависима.
Б0.Если к лин.зависим. системе векторов добавить 1 или несколько векторов, то вся система векторов будет лин.зависима.
В).Система векторов лин.завис,когда 1 из векторов явл. лин.комбинацией остальных векторов.
Г).2 вектора лин зависимы т и тт,к они коллинеарны. Д).3 вектора лин зависимы т и тт,к они компланарны.
5) Базис в пространстве. Декартов базис
Максимальный возможный набор линейнонезависимых элементов называется базисом. (Любая упорядоченная тройка некомпланарных векторов в пространстве называется базисом в пространстве.)
Декартов базис базис, в котором векторы i,j,k взаимно ортогональны и по модулю равны 1.
6) Декартова система координат
Декартова система координат совокупность декартова базиса и точки начала координат.
7) Проекция вектора на ось
Проекция вектора на ось x называется длина его составляющей A1B1по этой оси, взятаясознаком “+” или “”. Приэтомберется знак “+”, если направление A1B1 совпадает с направлением оси х, и знак “”, если эти направленияпротивоположны. Если A1B1 =0, проекция равна 0.
8) Геометрический смысл координат вектора
Коэффициенты в разложении вектора по базису называются координатами этого вектора в данном базисе.
Координаты вектора ā в декартовом прямоугольном базисе (i, j, k) есть проекции этого вектора на соответствующие координатные оси.
9)Геометрический смысл линейной зависимости двух векторов
Система векторов линейно зависима тогда и только тогда, когда эти векторы коллинеарны.
10)Геометрический смысл линейной зависимости трёх векторов
Система векторов линейно зависима тогда и только тогда, когда эти векторы компланарны.
11)Линейная зависимость 4х векторов
Любые четыре вектора линейно зависимы. Всякий вектор может быть единственным образом разложен по трем некомпланарным векторам.
12) Скалярное произведение векторов. Определение
Скалярным произведением 2х ненулевых векторов называется число, равное произведению длины векторов на cos угла между ними.
Скалярное произведение в механик связано с вычислением
работы силы a по перемещению материальной точки вдоль b .
13) Свойства скалярного произведения:
Для любых векторов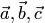 
и любого действительного числа 
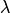: свойство коммутативности
свойство дистрибутивности
сочетательное свойство
скалярный квадрат вектора всегда больше 0
14)Вычисление угла между векторами
Углом между двумя ненулевыми векторами называетсявеличина образуемого ими угла, когда они отложены от одной точки. Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
15) Формула вычисления длины вектора через скалярное произведение
Скалярным произведением двух ненулевых векторов и
называется число, равное произведению длин этих векторов на косинус угла между ними:
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат. Длина (модуль) вектора, координаты которого известны, равен корню квадратному из суммы квадратов координат.
|
|
|
√x1x2 + y1y2 |
|
|a||b| = |
||||
cos φ |
||||
|
|
|
||
16) Формула длины вектора в декартовом базисе
Длина вектора в декартовом базисе на плоскости находится по формуле
Длина вектора в декартовом базисе в пространстве находится по формуле
17) Условия ортогональности 2х векторов
Два вектора a и b ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
18) Скалярное произведение векторов в декартовом базисе
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.
19) Векторное произведение векторов. Определение
Векторным произведением двух векторов 
и 
,заданных в прямоугольной системе координат трехмерного пространства,
называется такой вектор 
, что
● он является нулевым, если векторы 
и 
коллинеарны;
●он перпендикулярен и вектору 
и вектору 
(
);
его длина равна произведению длин векторов 
и 
на синус
угла между ними (
);
20) Свойство векторного произведения
1. вектор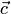 
ортогонален векторам 
и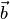 
2. его длина равна произведению длин векторов 
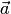и 
на
синус угла между ними: 
3. векторы 
, 
, 
(в указанном порядке) образуют правую
тройку.
4. 
5. 
6. 
21) Геометрический смысл векторного произведения
Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах.
22) Задача о вычислении площади треугольника с помощью векторного произведения
Площадь треугольника равна половине векторного произведения двух векторов (половине площади параллелограмма).
23) Коллинеарные векторы. Определение
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
24) Условие коллинеарности векторов
Для коллинеарности двух векторов 
и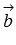 
необходимо и достаточно
1)чтобы они были связаны равенствами 
;
2)векторное произведение равнялось 0;
3)отношения их координат соответственно равны.
25)Смешанное произведение векторов. Определение
Смешанным произведением называется скалярное произведение 3 вектора на векторное произведение первых двух.
26)Свойства смешанного произведения
1)транспозиция (перестановка 2 векторов) a ∙ [b × c]= a∙[c×b] = b ∙ [a × c] = c ∙ [b × a];
2)инвариантность (циклическаяперестановка)a∙[b×c]=b∙[c× a] = c ∙ [a × b] ;
3)если смешанноепроизведениетрехненулевыхвекторовравно нулю, то эти векторы компланарные;
4)(λ[a×b],c )=λ([a×b],c)
5)(a1+ a2)b c = (a1×b )c + (a2×b )c
27)Геометрический смысл смешанного произведения
Модуль смешанного произведения равен объему параллелепипеда.
28)Задача о вычислении объема пирамиды с помощью смешанного произведения
Объем пирамиды равен смешанного произведения трех векторов. объема параллелепипеда.
29)Компланарные векторы. Определение
Векторы, параллельные одной плоскости или лежащие на одной плоскости называют компланарнымивекторами.
30)Условие компланарности векторов
1)Три вектора компланарны если их смешанное произведение равно нулю;
2)Три вектора компланарны если они линейно зависимы;
3)Вектора компланарны если среди них не более двух линейно независимых векторов.
31)Векторное произведение векторов в декартовом базисе
Векторным произведением a на b называется c , длина которого численно равна площади параллелограмма, построенного на
векторах a и b; c перпендикулярен к плоскости, в которой лежат
эти векторы и направлен так, чтобынаименьшеевращениеот a к b вокруг c осуществлялось против часовой стрелки, если смотреть с конца c .
Векторное произведение в декартовом базисе вектор, значение
которого можно вычислить по формуле: a×b = i(ab ab) j(ab
yz zy xz
ab) + k(ab ab)
zx xy yx
32) Смешанное произведение векторов декартовом базисе
Смешанным произведением называется скалярное произведение 3 вектора на векторное произведение первых двух.
([a×b],c)
Смешанное произведение равно определителю, строками которого являются координаты сомножителей.
33)Векторно параметрическое уравнение плоскости
M0 (x0;y0;z0) и M (x;y;z) ; a , b неколлинеарные векторы;
3 вектора компланарны, значит линейно зависимы; тогда один из них является линейной комбинацией 2 других.
r − r0 = pa + qb, где p, q параметры
r = r0 + pa + qb
или
[Система] x = x0 + pa1 + qb1; y = y0 + pa2 + qb2; z = z0 + pa3 + qb3;
34) Векторное уравнение плоскости
(Общее уравнение плоскости)
Ax +By +Cz +D = 0, где n = (A;B;C); A,B,C,D R
Нормальный вектор n ненулевой вектор, перпендикулярный плоскости.
r n = r0 n, где n вектор нормали; r0 радиусвектор точки α
r n = −D
35) Общее уравнение плоскости( координатная форма)
A(x −x0)+B(y −y0)+C(z −z0) = 0
M0 (x0;y0;z0) точка плоскости.
36)Уравнение плоскости в “отрезках на осях”. Геометрический смысл
коэффициентов
ax + by + zc = 1, где a,b,c отрезки, отсекаемые плоскостью на координатных осях.
−AD =a ; −BD =b ; −CD =c
37) Условие параллельности двух плоскостей
Плоскости, задаваемые в общей декартовой системе координат уравнениями Ax+By+Cz+D=0 и A1x+B1y+C1z+D1=0
параллельны тогда и т.тогда, когда сответствующие коэффициенты в их уравнениях пропорциональны, т.е. существует такое число k,
что А1=kA, В1=kB, С1=kC.
38) Условие совпадения двух плоскостей
Плоскости, задаваемые в общей декартовой системе координат уравнениями :Ax + By + Cz = 0 или A1x + B1y + C1z = 0 совпадают тогда и т.
тогда, когда существует такое число k, что 
=kA, 
=kB, 
=kC и
=kD
39) Условие пересечения 2х плоскостей
Две плоскости пересекаются если векторное произведение их нормалей не равно 0.
n n = c , |c |≠0
1 2
40) Условие перпендикулярности (ортогональности) 2х плоскостей
Еслиплоскости aи aвзаимноперпендикулярны, тоихнормальные
1 2
векторы n и n также перпендикулярны друг другу (φ = π/2), и
1 2
наоборот. Поэтому из формулы ( см. вопрос 41) непосредственно
получаем условие перпендикулярности плоскостей aи a:
1 2
AA+BB+CC=0
1 2 12 12
41) Угол между 2мя плоскостями |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим две плоскости a1 |
и a2 |
заданные соответствующими |
||||||||||||
уравнениями |
|
|
|
|
|
|||||||||
|
|
|||||||||||||
A x+B y+C z+D =0, |
A x+B y+C z+D =0. |
|
||||||||||||
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При любом расположении плоскостей a и a впространствеодинизуглов |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
φ между ними равен углу между их нормальными векторами |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||
n ={A ;B ;C } и |
n |
={A ;B ;C } и вычисляется по следующей формуле : |
||||||||||||
1 |
1 |
1 1 |
|
|
2 |
2 2 2 |
|
|
|
|||||
cos φ = |
|
n |
1 n2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|n1| |n2| |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|||
cos φ= |A ∙A |
+ B ∙B + C ∙C | |
|
|
|||
|
1 2 |
1 2 |
1 2 |
|
|
|
|
|
|
|
|
+ |
|
|
√A2 |
+ B 2 |
+ C 2√A2 |
|||
|
1 |
|
1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
B 2+C |
2 |
|
|
|
|
|
2 2 |
|
|
|
|
|
42) Векторнопараметрическое уравнение прямой в пространстве
Выводим формулу:
r r 0 || s t R: r r 0 =t*s
−теорема о линейной зависимости двух векторов−найдется такое t,что
r=r 0 +t*s векторнопарам уравнение прямой.
43) Каноническое уравнение прямой в пространстве
rr 0 ={x x0 ; y y0 ; z z0 }
s={m;n;l}могут равняться нулю! т.к. не делим
t= x−mx0 = y−ny0 = z−nz0
44) Векторное уравнение прямой в пространстве
(r r 0 )*s =0
r0 ,s однозначно определяют прямую
rрадиус вектор произвольной точки пространства
r0 указывает на точку прямой
rr 0 l rr 0 || s
45)Уравнение прямой на плоскости. Геометрический смысл коэффициентов в уравнении
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С,
получим: |
или |
, где |
|
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.