
- •26.Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые
- •Геометрический смысл определенного интеграла
- •27.Определенный интегралРимана. Свойстваопределенногоинтеграла.Теорема о среднем.
- •28.Определенный интеграл с переменнымверхнимпределом. Теорема о егопроизводной.Существованиепервообразной непрерывной функции.
- •Доказательство.
- •Разбиение промежутка интегрирования
- •29.Определенный интеграл с переменнымверхнимпределом. ФормулаНьютона- Лейбница.
- •Доказательство.
- •30.Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
- •Определенные интегралы (интеграл Римана).
- •31.Понятие о несобственныхинтегралах I-города. Интегралывида (a , p 0 ).
- •32.Понятие о несобственныхинтегралах II-города. Интегралывида
- •Несобственные интегралы второго рода
- •Полярная система координат и криволинейный сектор.
- •35.Вычисление объемовтелпоплощадямпоперечныхсечений и объемовтел
- •36.Функции двухпеременных. Передел и непрерывность.Частныепроизводные, их
- •40.Формула Тейлорадляфункциидвухпеременных.
- •41.Экстремумы функциидвухпеременных. Необходимоеусловиесуществования
- •42.Экстремумы функциидвухпеременных. Достаточноеусловиесуществования
- •44.Определение двойногоинтеграла.
- •Что значит вычислить двойной интеграл?
- •50.Вычисление тройногоинтеграла в цилиндрической системекоординат.
- •52.Приложения тройногоинтеграла.
32.Понятие о несобственныхинтегралах II-города. Интегралывида
(a, p 0 ).
Несобственные интегралы второго рода
Определение. Точка с называется особой
точкой функции f(x),
если 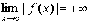 или
этот предел не существует. Ниже
рассматривается лишь первый случай.
или
этот предел не существует. Ниже
рассматривается лишь первый случай.
Пусть b есть
особая точка функции f(x)
и для любого 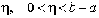 эта
функция интегрируема на отрезке
эта
функция интегрируема на отрезке 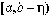 .
Тогда предел
.
Тогда предел
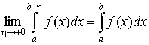
называется несобственным интегралом второго рода. Если этот предел существует и конечен, то говорят, что интеграл сходится или существует, если же этот предел равен бесконечности, то интеграл расходится, или не существует.
Аналогично, если особой точкой является а, то несобственный интеграл второго рода определяется так
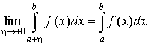 .
.
Наконец, если особая точка c удовлетворяет условию a<c<b, то интеграл определяется так
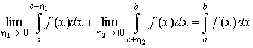 .
.
Заметьте,
что 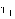 и
и 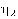 разные.
Если взять их одинаковыми, то получающийся
предел
разные.
Если взять их одинаковыми, то получающийся
предел
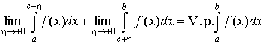
называется главным значением несобственного интеграла второго рода.
33.Кривые наплоскости и в пространстве. Спрямляемаякривая, длинадугикривой (выводформулыдляявнозаданной кривой).Дифференциалдлиныдуги.
34.Вычисление площадей плоскихфигур в декартовых и полярныхкоординатах.
Полярная система координат и криволинейный сектор.
Любая
точка в полярной системе координат
задается полярным углом 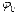 и
соответствующим полярным радиусом
и
соответствующим полярным радиусом 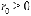 .
. 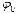 -
это угол, отсчитываемый от полярной оси
в положительном направлении (против
часовой стрелки), а
-
это угол, отсчитываемый от полярной оси
в положительном направлении (против
часовой стрелки), а 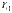 -
это расстояние от заданной точки до
начала координат (полюса).
-
это расстояние от заданной точки до
начала координат (полюса).
Если
функция 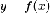 неотрицательна
на отрезке
неотрицательна
на отрезке 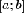 и
непрерывна на нем, то соответствующая
ей криволинейная трапеция квадрируема,
причемее площадь
и
непрерывна на нем, то соответствующая
ей криволинейная трапеция квадрируема,
причемее площадь  выражается
формулой
выражается
формулой

|
(4) |
Доказательство. Криволинейная
трапеция ограничена тремя отрезками и
графиком непрерывной функции  .
Как было показано в пункте 2 такая фигура
квадрируема. Чтобы вычислить площадь
этой трапеции, построим для нее внешние
и внутренние ступенчатые
фигуры(см. рис. 26).
.
Как было показано в пункте 2 такая фигура
квадрируема. Чтобы вычислить площадь
этой трапеции, построим для нее внешние
и внутренние ступенчатые
фигуры(см. рис. 26).
Тогда, с одной стороны, имеем:

где  —
площадь внутренней ступенчатой
фигуры,
—
площадь внутренней ступенчатой
фигуры,  —площадь
внешней ступенчатой фигуры,
—площадь
внешней ступенчатой фигуры,  и
и 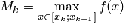 .
С другой стороны, по определению интеграла
можно записать:
.
С другой стороны, по определению интеграла
можно записать:

Таким
образом, числа  и
и  разделяют
одни и те же числовые множества:
разделяют
одни и те же числовые множества: 
 .
Но, как было показано при изучении
определенного интеграла, эти множества
разделяются лишь одним числом, и потому
.
Но, как было показано при изучении
определенного интеграла, эти множества
разделяются лишь одним числом, и потому  .
Теорема доказана.
.
Теорема доказана.
Аналогично
доказывается, что если фигура ограничена
снизу графиком функции 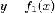 ,
сверху графиком функции
,
сверху графиком функции 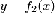 ,
а слева и справа прямыми
,
а слева и справа прямыми 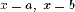 (рис.
30), то ее площадь выражается формулой
(рис.
30), то ее площадь выражается формулой

Наглядный
смысл формулы (4) состоит в том, что
криволинейную трапецию можно рассматривать
как объединение «бесконечно тонких
полосок» с основаниями 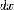 и
высотами
и
высотами 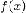 .
.

Пусть
теперь функция 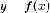 непрерывна
на отрезке
непрерывна
на отрезке 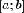 и
принимает на нем только неположительные
значения. Выразим с помощью определенного
интеграла площадь соответствующей
криволинейной трапеции
и
принимает на нем только неположительные
значения. Выразим с помощью определенного
интеграла площадь соответствующей
криволинейной трапеции 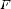 .
.
Рассмотрим
фигуру 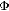 ,
симметричную фигуре
,
симметричную фигуре 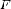 относительно
оси
относительно
оси 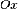 .
Эта фигура (рис. 31) представляет собой
криволинейную трапецию, ограниченную
сверху графиком непрерывной на
отрезке
.
Эта фигура (рис. 31) представляет собой
криволинейную трапецию, ограниченную
сверху графиком непрерывной на
отрезке 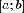 функции
функции 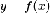 ,
которая на
,
которая на  принимает
только неотрицательные значения. По
доказанному выше
принимает
только неотрицательные значения. По
доказанному выше

 .
Но
.
Но 
Значит,

Как
мы видим, в рассматриваемом случае
интеграл  дает
значение площади криволинейной
трапеции
дает
значение площади криволинейной
трапеции 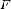 с
точностью до знака. Если же функция
с
точностью до знака. Если же функция 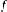 меняет
знак на отрезке
меняет
знак на отрезке  в
конечном числе точек, то значение
интеграла
в
конечном числе точек, то значение
интеграла  дает
алгебраическую сумму площадей
соответствующих криволинейных трапеций,
ограниченных частями графика функции
дает
алгебраическую сумму площадей
соответствующих криволинейных трапеций,
ограниченных частями графика функции 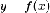 ,
отрезками оси
,
отрезками оси 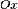 и,
быть может, отрезками, параллельными
оси
и,
быть может, отрезками, параллельными
оси 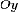 (рис.
32).
(рис.
32).
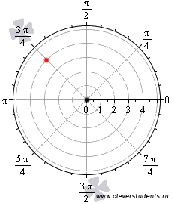
На
рисунке полюс изображенчерной точкой,
полярная ось – черным жирным лучом, а
красная точка определяется углом  и
расстоянием до полюса
и
расстоянием до полюса 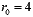 .
.
На практике очень часто полярную систему координат рассматривают вместе с прямоугольной декартовой, совмещая начала координат и полярную ось с осью абсцисс.
Связь
декартовых и полярных координат задается
соотношениями 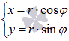 и
обратно
и
обратно 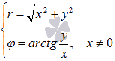 .
.
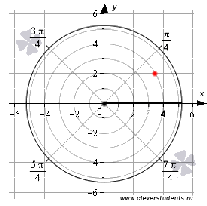
На
чертеже красная точка имеет координаты 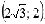 ,
а в полярной системе координат определяется
углом
,
а в полярной системе координат определяется
углом  и
расстоянием до полюса
и
расстоянием до полюса 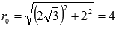 .
.
В
полярной системе координат равенство 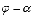 задает
луч, выходящий из полюса и составляющий
угол
задает
луч, выходящий из полюса и составляющий
угол 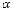 с
полярной осью (
с
полярной осью (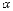 задается
в радианах или градусах). Полярная ось
задается уравнением
задается
в радианах или градусах). Полярная ось
задается уравнением  .
Равенство
.
Равенство 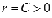 задает
окружность с центром в начале координат
радиуса C. В свою очередь
функция
задает
окружность с центром в начале координат
радиуса C. В свою очередь
функция 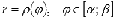 определяет
некоторую линию в полярных координатах.
определяет
некоторую линию в полярных координатах.
Обратите
внимание, что мы будем считать
функцию 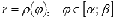 всегда
НЕОТРИЦАТЕЛЬНОЙ, так как с геометрической
позиции она задает расстояние от полюса
до точки для данного значения угла
всегда
НЕОТРИЦАТЕЛЬНОЙ, так как с геометрической
позиции она задает расстояние от полюса
до точки для данного значения угла 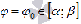 .
Однако, иногда рассматривают и
отрицательные значения функции
.
Однако, иногда рассматривают и
отрицательные значения функции 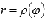 ,
так что желательно уточнить у преподавателя
его отношение к этому вопросу.
,
так что желательно уточнить у преподавателя
его отношение к этому вопросу.
Ниже на рисунке приведены несколько примеров линий в полярной системе координат.
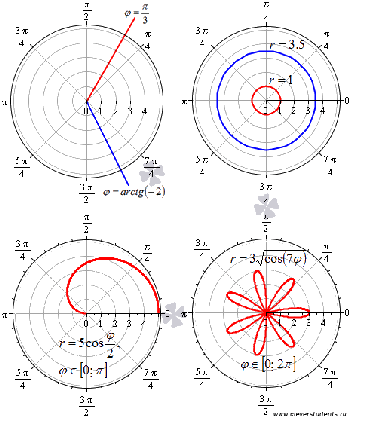
Если
функция 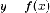 неотрицательна
на отрезке
неотрицательна
на отрезке 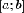 и
непрерывна на нем, то соответствующая
ей криволинейная трапеция квадрируема,
причемее площадь
и
непрерывна на нем, то соответствующая
ей криволинейная трапеция квадрируема,
причемее площадь  выражается
формулой
выражается
формулой

|
(4) |
Доказательство. Криволинейная
трапеция ограничена тремя отрезками и
графиком непрерывной функции 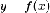 .
Как было показано в пункте 2 такая фигура
квадрируема. Чтобы вычислить площадь
этой трапеции, построим для нее внешние
и внутренние ступенчатые
фигуры(см.
рис. 26).
.
Как было показано в пункте 2 такая фигура
квадрируема. Чтобы вычислить площадь
этой трапеции, построим для нее внешние
и внутренние ступенчатые
фигуры(см.
рис. 26).
Тогда, с одной стороны, имеем:

где  —
площадь внутренней ступенчатой
фигуры,
—
площадь внутренней ступенчатой
фигуры,  —площадь
внешней ступенчатой фигуры,
—площадь
внешней ступенчатой фигуры,  и
и 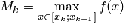 .
С другой стороны, по определению интеграла
можно записать:
.
С другой стороны, по определению интеграла
можно записать:

Таким
образом, числа  и
и  разделяют
одни и те же числовые множества:
разделяют
одни и те же числовые множества: 
 .
Но, как было показано при изучении
определенного интеграла, эти множества
разделяются лишь одним числом, и потому
.
Но, как было показано при изучении
определенного интеграла, эти множества
разделяются лишь одним числом, и потому  .
Теорема доказана.
.
Теорема доказана.
Аналогично
доказывается, что если фигура ограничена
снизу графиком функции 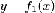 ,
сверху графиком функции
,
сверху графиком функции 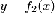 ,
а слева и справа прямыми
,
а слева и справа прямыми 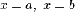 (рис.
30), то ее площадь выражается формулой
(рис.
30), то ее площадь выражается формулой

Наглядный
смысл формулы (4) состоит в том, что
криволинейную трапецию можно рассматривать
как объединение «бесконечно тонких
полосок» с основаниями 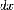 и
высотами
и
высотами 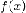 .
.

Пусть
теперь функция 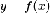 непрерывна
на отрезке
непрерывна
на отрезке 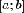 и
принимает на нем только неположительные
значения. Выразим с помощью определенного
интеграла площадь соответствующей
криволинейной трапеции
и
принимает на нем только неположительные
значения. Выразим с помощью определенного
интеграла площадь соответствующей
криволинейной трапеции 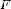 .
.
Рассмотрим
фигуру 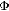 ,
симметричную фигуре
,
симметричную фигуре 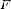 относительно
оси
относительно
оси 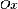 .
Эта фигура (рис. 31) представляет собой
криволинейную трапецию, ограниченную
сверху графиком непрерывной на
отрезке
.
Эта фигура (рис. 31) представляет собой
криволинейную трапецию, ограниченную
сверху графиком непрерывной на
отрезке  функции
функции 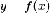 ,
которая на
,
которая на 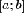 принимает
только неотрицательные значения. По
доказанному выше
принимает
только неотрицательные значения. По
доказанному выше

 .
Но
.
Но 
Значит,

Как
мы видим, в рассматриваемом случае
интеграл  дает
значение площади криволинейной
трапеции
дает
значение площади криволинейной
трапеции 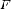 с
точностью до знака. Если же функция
с
точностью до знака. Если же функция 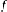 меняет
знак на отрезке
меняет
знак на отрезке 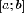 в
конечном числе точек, то значение
интеграла
в
конечном числе точек, то значение
интеграла  дает
алгебраическую сумму площадей
соответствующих криволинейных трапеций,
ограниченных частями графика функции
дает
алгебраическую сумму площадей
соответствующих криволинейных трапеций,
ограниченных частями графика функции  ,
отрезками оси
,
отрезками оси  и,
быть может, отрезками, параллельными
оси
и,
быть может, отрезками, параллельными
оси 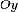 (рис.
32).
(рис.
32).
