Найдем яркость рассеивателя. Поток Φ создает освещенность E = dSΦ ,

следовательно, поток, упавший на рассеиватель:

где E – освещенность, создаваемая падающим потоком, α – коэффициент Альбедо.

2.6. Освещенность, создаваемая различными источниками (закон обратных квадратов)

2.6.1. Освещенность, создаваемая точечным источником

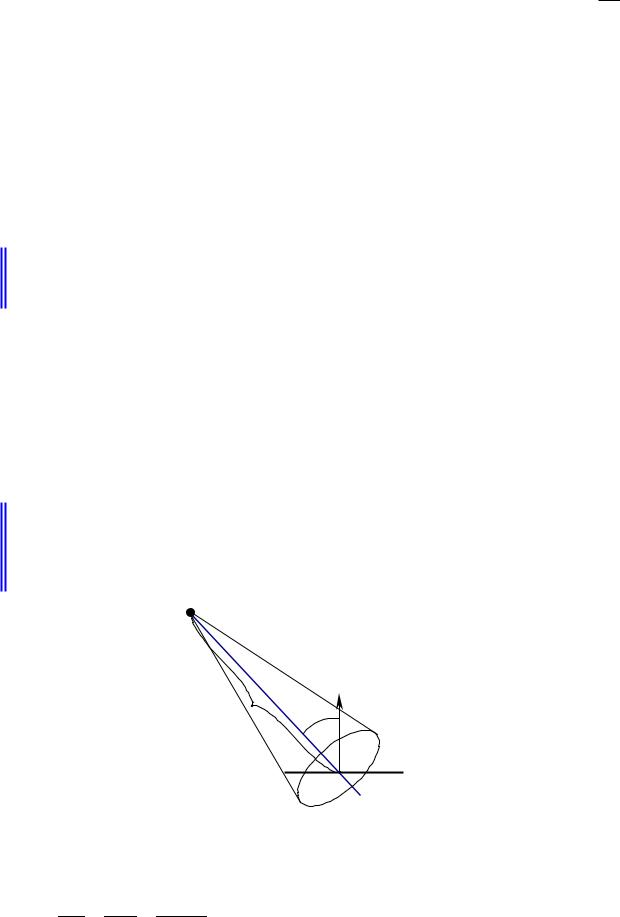
Рассмотрим точечный источник.

Точечный источник – это источник, размерами которого можно пренебречь по сравнению с расстоянием до него, и который излучает поток, равномерный по всем направлениям.

I

Рис.2.6.1. Освещенность, создаваемая точечным источником.

Освещенность площадки dS , создаваемая точечным источником:

E = ddSΦ = IddSΩ = I cosr2 θ

36

Закон обратных квадратов:

Освещенность, создаваемая точечным источником обратно пропорциональна расстоянию от источника до поверхности и прямо пропорционально косинусу угла, между направлением светового потока и нормалью к освещаемой поверхности:

где I – сила света источника в направлении освещаемой точки. Практические измерения показывают, что для соблюдения закона

обратных квадратов отношение размера источника к расстоянию до него должно быть меньше 0.1.

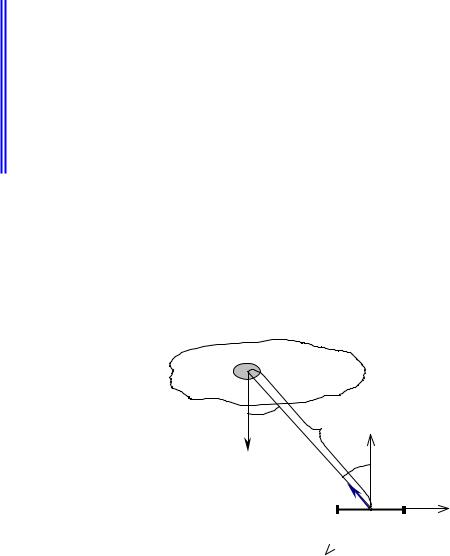
2.6.2. Освещенность от протяженного ламбертовского источника

dS

q E y

x

Рис.2.6.2 Освещенность от протяженного ламбертовского источника.

Для протяженного источника можно разбить поверхность источника на элементарные площадки dS (рис.2.6.2) и определить освещенность, создаваемой каждой из них по закону обратных квадратов (2.6.1):

Проинтегрируем теперь элементарную освещенность по всей площади источника:

Так как у ламбертовского источника яркость постоянна по всем направлениям, ее можно вынести за интеграл:

37

направляющие косинусы.

Можно показать, что выражения (2.6.4) и (2.6.5) эквивалентны, если учесть, что dqx = −sinαxdαx , dqy = −sinαydαy , dαxdαy = dΩ, а углы β и θ являются дополнительными к αx , αy .

38