35782

Используя уравнение (6.16) совместно с уравнениями (6.13) и (6.14),

а это приводит к выводу зависимости для толщины δ:

6.4. Гидравлическое сопротивление плоской пластины

Полученное решение для распределения скоростей позволяет легко вычислить сопротивление трения. Силы сопротивления вычисляются по касательным напряжениям на поверхности. На расстоянии x от передней кромки они равны

вычислим производную:

vyx = v0 ηf ′ηy = v0f ′′ηy .

Найдем величину ηy :

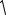η = y νvx0 , ηy = νvx0 .

и значение производной

dvdyx = v0 f ′′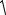 νvx0

Величину f ′′ найдем из степенного ряда (6.15)

Как следует из формулы (6.19), величина f ′′η=0 = 2A , и

62

Касательное напряжение на поверхности пластины будет

τs = 2μAv0 νvx0 .

Подставив в это уравнение численное значение постоянной А, получим

Напомним, что эта и выведенные ранее формулы применимы только к ламинарному пограничному слою, когда число Рейнольдса ReL ≤ 5 105 . Формулы (6.20) и (6.21) подтверждены многочисленными опытами.

Полученное Блаузиусом решение задачи о ламинарном пограничном слое показывает, что, даже в совершенстве владеющий предметом математик не в состоянии решить общих уравнений Навье-Стокса. На самом деле при решении приведенной выше простой задачи обтекания плоской пластины нужно качественно знать общую картину течения, обладать интуицией, чтобы без ущерба для точности отбрасывать отдельные члены уравнения и делать удачные подстановки при анализе дифференциальных уравнений.

63

Глава 7. Описание движения жидкости с помощью интегродифференциального уравнения

7.1. Уравнение Кармана для изотермического течения

Примеры точного решения уравнений пограничного слоя показывают, что их интегрирование сопряжено с большими математическими трудностями. Между тем, для практических целей важен общий случай обтекания для тел любой формы при любом режиме течения. Изложенные выше аналитические методы не позволяют решить эту задачу. Поэтому возникает необходимость найти приближенные методы расчета пограничного слоя.

Как показали Т.Карман (1921) и К.Польгаузен, можно предложить простой приближенный метод, если отказаться от удовлетворения дифференциальных уравнений пограничного слоя для каждой отдельной жидкой струйки и вместо этого ограничиться удовлетворением этих уравнений только в среднем по толщине пограничного слоя. Для этой цели следует заменить дифференциальные уравнения интегральными соотношениями, получившимися из уравнения движения путем его интегрирования по толщине пограничного слоя.

Введем интегральное уравнение для случая обтекания пластины несжимаемой жидкостью ( div v = 0 ) в продольном направлении, когда давление и скорость вдоль координаты x остаются неизменными. Будем исходить из уравнения Навье-Стокса (6.3):

Запишем второй член уравнения (7.2) с учетом (7.4):

64

Рассмотрим третий член уравнения (7.2) и обратим внимание на то, что вне пограничного слоя скорость постоянна, т.е. ∂vx / ∂y = 0 , и, как было показано в разделе 6.1, члены с вязкостью равны нулю, т.е. уравнение (6.3) приобретает вид

vx ∂∂vxx = ρ1 ∂∂px или 12 ∂∂vxx2 = ρ1 ∂∂px .

Напомним, что решение данного уравнения приводит к уравнению Бернулли, т.е.

ρv202 + p = const,

что позволяет записать

65

Полученное уравнение называют интегральным соотношением Кармана для безградиентного течения ( ∂p / ∂x = 0 ) пограничного слоя. Это условие пригодно для ламинарного и турбулентного течения жидкости. Однако вид функций vx = vx ( y) , способ их выбора, а также метод определения касательных напряжений τw будут различными для

ламинарного и турбулентного режимов течения. Поэтому решение интегральных соотношений для этих двух видов течения рассмотрим отдельно.

7.2. Решение уравнения Кармана для пластины

Заметим, что в уравнении (7.9) искомой величиной является толщина пограничного слоя δ, а распределение скорости vx - по толщине

где a, b, c, d – постоянные коэффициенты. Для определения постоянных коэффициентов в (7.10) используются граничные условия (7.1) на поверхности пластины y=0 и на внешней границе пограничного слоя y=δ. При y=0

последнее условие следует из уравнения (6.7), если его записать для y=0 и учесть, что ∂p / ∂x = 0 , то все члены, кроме последнего, обратятся в нуль. При y=δ

т.к. происходит плавный переход кривой vx = vx ( y) к вертикальной прямой v0 = const на внешней границе пограничного слоя.

Используя граничные условия (7.11) и (7.12), легко найти постоянные коэффициенты уравнения (7.10). Соответствующие преобразования приводят к искомой функции распределения продольной скорости vx по толщине пограничного слоя:

Подставляя в (7.9) выражение (7.13), получим

Найдем касательное напряжение на поверхности пластины:

66

Интегральное соотношение (7.9) с учетом двух последних зависимостей переходит в дифференциальное уравнение:

Размещая начало координат на передней кромке пластины, получим граничное условие:

Учитывая уравнение (7.18), из (7.14) получим

Среднее значение коэффициентов трения для всей пластины длиной l и шириной, равной l определяется из выражения

Выражение (7.20) получено Блаузиусом для сопротивления продольно обтекаемой пластины при ламинарном течении; формула (7.20) справедлива для чисел Рейнольдса

7.3. Уравнение Г.Н. Кружилина для неизотермической жидкости

Это уравнение позволяет получить не локальные, а средние по толщине пограничного слоя скорости и температуры, а по длине пограничного слоя эти зависимости получаются точно.

67

Рассмотрим теплообмен пластины, продольно обтекаемой потоком несжимаемой жидкости ( div v = 0 ), в стационарном режиме ( ∂∂τt = 0 ).

Рассмотрим следующие преобразования:

Сложим эти два равенства:

С учетом уравнения (5.7,б) первое слагаемое в правой части обращается в нуль, и уравнение (7.22) можно записать следующим образом:

Проинтегрируем выражение (7.23) по толщине δ термического пограничного слоя

Второе слагаемое в левой части обращается в нуль, так как

что позволяет записать последнее выражение в виде

Это выражение носит название интегродифференциального уравнения теплового потока и впервые было получено в 1936 г. Г.Н.Кружилиным.

68

7.4. Теплообмен при ламинарном течении жидкости вдоль пластины

Для ламинарного течения жидкости вдоль пластины известно

где δ - толщина гидродинамического пограничного слоя, которая может быть найдена из формулы (7.17)

Найдем теперь распределение температур в пограничном слое. Зададим это распределение в виде полинома третьей степени, который описывает монотонный ход кривой

где a, b, c и d – постоянные коэффициенты этого полинома определяются из следующих граничных условий

Четвертое условие найдем из уравнения (7.22), записанного для скорости пограничного слоя на поверхности y=0, где vx = vy = 0 . Получаем

Из условий (7.26), (7.27) нетрудно получить постоянные коэффициенты, и уравнение (7.25) приобретает следующий вид:

Найдем из этого условия значение производной на поверхности y=0:

воспользуемся интегродифференциальным уравнением (7.24), в которое