Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

лінійна алгебра та аналітична геометрія

.pdf

Скачиваний:

302

Добавлен:

17.03.2016

Размер:

10.08 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 238 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

8. Координати

Розгляньмо довільну точку M на площині і розк-

ладімо її радіус-вектор

rM OM за базисом {i , j }

(рис. 8.7):

OM OMx

OMy xi

yj .

Рис. 8.7

Координатами точки M у ПДСК Oij

називають коор-

Означення 8.5.

динати її радіуса-вектора

rM у базисі {i , j } і записують

M M(x;y).

Першу координату називають абсцисою, другу — ординатою.

Координатні осі розбивають площину на чотири частини, які називають

координатними чвертями (квадрантами). Кожній чверті відповідає певна комбінація знаків координат (рис. 8.8).

Розгляньмо лінії, які мають у ПДСК найпростіший вигляд,— їх ще на-

зивають координатними лініями.

Координатними лініями, тобто лініями з найпростішими рівняннями у

ПДСК, є вертикальні прямі x a,a ,

та горизонтальні прямі

y b,b (рис. 8.9).

III

Рис. 8.8

Рис. 8.9

Прямокутна декартова система координат у просторі

Зафіксуймо у просторі точку O і виберімо за базис трійку взаємно перпендикулярних одиничних векторів (рис. 8.10):

i OE1, j OE2 та k OE3 .

У цьому разі кажуть, що у просторі задано прямокутну декартову сис-

тему координат Oijk (Oxyz ). Точку O називають початком координат. Осі,

що проходять через початок координат з напрямними векторами i , j та k ,

називають осями координат: першу — віссю абсцис Ox, другу — віссю орди-

нат Oy, третю — віссю аплікат Oz. Площини, що проходять через осі координат, називають координатними площинами, відповідно Oxy,Oxz та Oyz.

72	Розділ 2. Методи й моделі векторної алгебри

Координатні площини розбивають простір на вісім частин — октантів, які нумерують як на рис. 8.11 (у першому октанті — всі три координати додатні,…).

	z
	E3	III		II
	k	IV	z	I
	k
	O	E2	x		y
E1	j	y	x	O	y
E1	i	VII			VI
x	Рис. 8.10	VIII			V
	Рис. 8.10	Рис. 8.11
		Рис. 8.11

Розгляньмо довільну точку M у просторі і розкладімо її радіус-вектор

rM OM за базисом {i , j ,k } (рис. 8.12):

OM OMx OMy OMz xi yj zk .

Означення 8.6. Координатами точки M у ПДСК Oijk називають коор-

динати її радіуса-вектора rM у базисі {i , j ,k } і записують

M M(x;y;z).

Першу координату називають абсцисою, другу — ординатою, третю —

аплікатою.

		z
		Mz
						M

		k

					rM
			O				My y
			O			j	My y
Mx

	i
x
				Рис. 8.12

8. Координати

8.4. Найпростіші задачі аналітичної геометрії

Координати вектора

Нехай у ПДСК Oxyz задано дві точки

A(xA;yA;zA) та B(xB ;yB ;zB ). З означення координат точки і теореми 8.2 маємо (рис. 8.13):

xB xA

AB r r y

B A

rB B

Рис. 8.13

Висновок. Щоб знайти координати вектора, треба від координат його кінця відняти координати початку.

Це ж правило правдиве й для просторів вимірності 1 та 2 — на прямій і на площині відповідно.

Поділ відрізка в заданому відношенні

Кажуть, що точка M поділяє відрізок A1A2 у відношенні 1,

якщо

виконано співвідношення

A1M MA2.

Нехай точка M (x;y;z) поділяє відрізок A1A2,

який з’єднує точки A (x

;y ;z

) та A (x

), у

1 1

відношенні (рис. 8.14). Розгляньмо

вектори

A1M та MA2.

Рис. 8.14

Оскільки

x x1

A M y y

;

MA y

y ,

z z

то

x x1

x2 x

(x2 x)

y y

z z

Приклад застосування подано у п. 12.4.

74	Розділ 2. Методи й моделі векторної алгебри


x x		1
		1


y y
	1

z z	1
	1

(x				x);		)x (x			x			);
(x			2	x);	(1	)x (x		1	x			);
			2					1	2

(y				y);		)y (y			y		);
(y		2		y);	(1	)y (y			y		);
		2					1		2
(z				z).		)z (z			z	).
(z	2			z).	(1	)z (z	1		z	).
	2						1		2


Якщо 1, то A1M MA2					0, тобто A1A2 0						(маємо випадок
виродженого відрізка — немає що ділити).
Отже, для ненульового відрізка, якщо 1,								маємо

	x	x1 x2	;y	y1 y2		;z	z1	z2	.	(8.1)
	x		;y			;z			.	(8.1)
		1			1		1

Зауваження 8.3.

1.Якщо 0, то це означає, що точки A1 та M збігаються (рис. 8.15).

2.Якщо 0, то точка M лежить усередині відрізка A1A2 (рис. 8.15).

3.Якщо 0, то точка M лежить ззовні відрізка A1A2 і кажуть, що во-

на поділяє відрізок зовнішнім чином (рис. 8.15).

4. Якщо 1,	точка M є серединою відрізка A1A2 (рис. 8.15).
Отже, координати середини відрізка A1A2							знаходять за формулами:

		x	x1 x2	,y	y1 y2			,z	z1	z2	.		(8.2)
		x	2	,y				,z		2	.		(8.2)
			2			2				2
0				0						0
A M		A	A1		M A			A1				A2	M
1	2			1		2
				1
			A1	M			A2
				Рис. 8.15

F M D

A E C

Рис. 8.16

Приклад 8.2. Знайдімо координати вектора AB, середини відрізка BC і точки перетину медіан M три-

кутника	ABC	з	вершинами	A(2;1; 3),
B(4; 3; 4),C(8; 1; 4) (рис. 8.16).

		4	2		2
		4	2		2



		3	1		2
Координати вектора AB		3	1		2	.


	4		3	1

Середина відрізка BC точка D має координати:

9. Скалярне множення геометричних векторів

					x			x				4 8
					x	B		x				4 8
xD						B			C					6;
xD														6;
								2			2
								2			2
					yB yC							3 1
yD					yB yC							3 1		1;				D 6;1; 4 .


								2			2
								2			2
					zB zC							4	4
					zB zC							4	4
z	D													4.
z														4.
								2			2
								2			2
Точка M поділяє відрізок AD у відношенні 2. Отже, точка M
має координати:
	x			2x						2 2 6 14
xM			A					D
xM																	;
			1 2								3				3
			1 2								3				3
	yA			2yD						1 2 1										11
	yA			2yD						1 2 1								14		11
yM													1;					M	;1;		.
yM													1;					M	;1;		.
			1 2							3										3
			1 2							3								3		3
	z			2z						3 2 4					11
	z	A		2z			D			3 2 4					11
zM		A					D									.
zM			1	2							3				3	.
			1	2							3				3

9. Скалярне множення геометричних векторів

9.1. Проекція вектора на вісь

Ортогональною проекцією точки M простору (площини) на пряму L на-

зивають точку M перетину прямої із площиною (прямою), що проходить через точку M перпендикулярно до прямої L (рис. 9.1, рис. 9.2).

Нехай задано вісь L з напрямним вектором s . Розгляньмо вектор

a AB. Ортогональними проекціями точок A та B на вісь L є відповід-

но точки A та B (рис. 9.3).

M B

M
M					a			L
				A				L
		M		A				B

						a	L	s
			L			A
M	L					A
M	L
Рис. 9.1		Рис. 9.2				Рис. 9.3

Векторною проекцією вектора a AB на вісь L s називають вектор aL A B .

76	Розділ 2. Методи й моделі векторної алгебри

Означення 9.1. Проекцією (скалярною проекцію) вектора a AB на вісь L з напрямним вектором s називають число

prL a prs a ,

таке, що

A B s 0,s 0 ss .

Число prs a називають ще проекцією вектора a на напрям вектора s ,

причому:

A B

якщо s A B ,

(s , A B ) 2 ,

якщо s A B .

Твердження 9.1 (властивості проекції вектора).

Проекція вектора a на вісь L(s ) дорівнює добуткові довжини вектора a на косинус кута між вектором a та віссю (рис. 9.4):

prL a a cos(a,L) a cos(a,s ).

Рівні вектори мають рівні проекції на одну й ту саму вісь:

ab prL a prL b .

Проекція суми векторів на довільну вісь дорівнює сумі їхніх проекцій на цю вісь (рис. 9.5):

prL(a b ) prL a prL b .

Якщо помножити вектор на число, то проекція вектора на вісь теж помножиться на це число (рис. 9.6):

prL( a) prL a.

prL a

pr a

Рис.9.4

9. Скалярне множення геометричних векторів

A b

a A

B s

Рис. 9.5

Рис. 9.6

cos .

Якщо (a, s )

2 , то prL a

, то prL a 0

cos .

Якщо (a,s )

Якщо (a, s )

, то prL a

cos( )

Справді, якщо a

b, то

та (a, L) (b, L),

випливає, що prL a prL b .

cos .

звідси із властивості 1

Утворімо ламану OAB з ланками OA a та AB b (рис. 9.5). Спроектувавши точки O,A,B на вісь L(s ), дістанемо точки O ,A ,B .

Нехай prL a та prL b . Тоді O A s 0,A B s 0. Звідси

O B ( )s,

але ця рівність означає, що є проекцією вектора OB a b . Тобто prL(a b ) prL a prL b .

У разі 0 властивість очевидна — проекція нуль-вектора дорівнює нулю.

		Нехай вектор a	AB утворює з	віссю L кут і нехай 0. Тоді вектор
		утворює з віссю L той самий кут		, а вектор (		) — кут ( ). Тоді із
	a				a
властивості 1 випливає, що

prL( a ) AB cos AB cos prL a;

prL( a ) AB cos( ) AB cos prL a.

Наслідок із твердження 9.2. Лінійним діям над векторами відповідають такі самі лінійні дії над проекціями цих векторів на довільну вісь.

9.2. Скалярний добуток двох векторів

Означення 9.2. Скалярним добутком двох векторів a та b називають число, що дорівнює добуткові довжин цих векторів на косинус кута між ними і позначають

def

(a,b ) a b cos(a,b ).

Приклад простору зі скалярним добутком (евклідового простору) подано в п. 13.7.

78 Розділ 2. Методи й моделі векторної алгебри

Якщо хоча б один з векторів нульовий, то кут не визначений, і скалярний добуток вважають рівним нулю.

Скалярний добуток векторів a та b позначають ще як a b.

Вектори a та b називають ортогональними, якщо (a,b ) 0 і позна-

чають a b. Нульовий вектор є ортогональним (і його можна вважати перпендикулярним) до будь-якого вектора.

З означення 9.2 скалярного добутку і твердження 9.1 випливає, що

(a,b ) a pra b b prb a.

Твердження 9.2

властивості скалярного множення

Для будь-яких

(

та

векторів

,b,

будь-яких дійсних чисел та :

(

) (комутативність скалярного множення);

) (b,

(

, b

) (

,b ) (однорідність скалярного множення);

(a b,c ) (a

,c ) (b,c ),



(дистрибутивність скалярного множення);

(

)

(

,b ) (

(

2 0,(

(додатна визначеність скаляр-

)

) 0 a

ного добутку).

Наслідки із твердження 9.2.

Завдяки властивостям скалярного добутку лінійні комбінації векторів можна перемножувати скалярно як лінійні многочлени.

Правдива формула для довжини вектора:

(

Приклад 9.1.

Знаючи, що

, обчислімо: 1)

5,(a,b )

(a,b );

; 3) pr

; 4) prb

1. (a,b )

cos(a,b )

5 cos 3 5.

2. Використовуючи властивості лінійності та комутативності скалярного добутку, маємо:

a b (a b ,a b ) 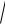(a,a ) (b,a ) (a,b ) (b,b )

22 2 5 52

39.

2(a,b )

cos(a,b ) 2 cos

prb

) 2 prb

3 prb

2 1 3 5 17.

9. Скалярне множення геометричних векторів

Зауваження 9.1.

1.Скалярний добуток двох векторів є числом — об’єктом іншої природи ніж множники.

2.Рівність (x ,y ) 0 виконано не лише для x 0 або y 0, а й для

ненульових перпендикулярних векторів.

3. Можна запровадити лише «скалярний квадрат» вектора: x 2 (x, x ). Не існує скалярного добутку трьох і більше векторів.

Скалярний добуток в ортонормованому базисі

Означення 9.3. Базис називають ортонормованим, якщо його вектори попарно ортогональні і мають одиничну довжину.

З означення випливає, що вектори ортонормованого базису

		1				0				0




		0								0
i				, j 1				,k


	0				0				1

			{i , j ,k }				{i ,j ,k }				{i ,j ,k }

справджують таку таблицю скалярного множення:

(,)
(,)				i		j	k

				1	0		0
		i		1	0		0	.

				0	1		0
			j	0	1		0

				0	0		1
	k			0	0		1

Нехай задано координати векторів a та b в ортонормованому базисі

{i , j ,k }:

;

a ax i ay j azk ay

{

,k }

b b i

b j

b k

{

,k }

За властивостями скалярного добутку маємо

(a,b ) (ax i ay j azk ,bx i by j bzk )

axbx (i , i ) ayby(j , j ) azbz (k ,k )

(axby aybx )(i , j ) (axbz azbx )(i ,k )

(aybz azby )(j ,k ).

80 Розділ 2. Методи й моделі векторної алгебри

З таблиці скалярного множення випливає, що

(a,b ) axbx ayby azbz a b .

Тоді довжину вектора a зі стовпцем координат a в ортонормованому базисі можна знайти за формулою:

a (ax )2 (ay )2 (az )2 .

						2			3
						2			3


Приклад 9.2. Знайдімо (a,b ),
Приклад 9.2. Знайдімо (a,b ),	a	, pr	b	для векторів a 1			,b	1		.
		a
		a

					5			1

				3
				3

	2

(a,b ) a b		1			2 3 ( 1) 1 5 1	10;
(a,b ) a b		1	5 1		2 3 ( 1) 1 5 1	10;


			1

22 ( 1)2

30;

(

)

.

9.3. Напрямні косинуси вектора

Розгляньмо ПДСК з ортонормованим базисом

{i , j ,k } (рис. 9.7) і вектор

a a

i a j a

z {i ,j ,k }

Помножмо вектор

скалярно послідовно на

x ax

Рис. 9.7

вектори i , j

та k

і врахуймо означення скалярно-

го добутку та проекції вектора на напрям:

(a, i )

cos(a, i )

;

(a, j )

cos(a, j )

ay;

az .

(a,k )

cos(a,k )

prk a

Твердження 9.3. Координати вектора в ортонормованому базисі дорівнюють проекціям вектора на координатні осі.

Якщо вектор утворює гострий (тупий) кут з координатною віссю, то його відповідна координата додатна (від’ємна).

Приклад застосування подано в п. 12.5.

<<< < Предыдущая 1 2 3 4 5 6 78 / 238 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.2019190.46 Кб4Л1.doc
#
18.07.2019895.49 Кб52Л10 Напр микр ЛАСР.doc
#
12.05.2015549.04 Кб8Л4 метрология.pdf
#
18.09.201960.93 Кб3Л6 Створення ТЗИ на ОИД.doc
#
18.09.2019194.05 Кб4Л7 Створення ТЗИ на ОІД передпроектн роботи.doc
#
17.03.201610.08 Mб302лінійна алгебра та аналітична геометрія.pdf
#
14.08.2019490.5 Кб2Лаб 1-5-IEE.doc
#
16.11.2019169.98 Кб1лаб 2 ПАХВ.doc
#
28.04.2019226.3 Кб3лаб 7.doc
#
14.11.20191.36 Mб4лаб работы анализ.docx
#
10.11.2019153.09 Кб4Лаб роб 6 Обчислення арифметичних виразів.doc