
Лекции_СС
.pdfПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ЦИФРОВЫХ АВТОМАТАХ Системы счисления
Для удобства последующего преобразования дискретный сигнал подвергается кодированию. Большинство кодов основано на системах счисления, причем использующих позиционный принцип образования числа, при котором значение каждой цифры зависит от ее положения в числе.
Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.
Существуют позиционные и непозиционные системы счисления.
Примером непозиционной системы является римская, в которой в качестве цифр используются некоторые буквы: I(1), V(5), X(10), L(50), C(100), D(500), M(1000). Значение цифры не зависит от ее положения в числе. Например, в числе
ХХХ цифра Х встречается трижды, и в каждом случае обозначает одну и ту же величину 10, а в сумме ХХХ – 30.
Величина числа в римской системе счисления определяется как сумма или разность чисел. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.
Например:
1998=MCMXCVIII=1000+(1000–100)+(100–10)+5+1+1+1
2002=MMII=1000+1000+1+1
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая – 7 единиц, а третья – 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 102 + 5 101 + 7 100 + 7 10–1 = 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления – количество различных цифр,
используемых для изображения чисел в данной системе счисления.
За основание системы можно принять любое натуральное число – два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.
Для позиционной системы счисления справедливо равенство (развернутая форма числа).
A |
= a |
n |
qn + a |
qn −1 |
+... + a q1 |
+ a q0 |
+ a |
q−1 |
+... + a |
− m |
q− m |
, |
(1) |
(q) |
|
|
n −1 |
1 |
0 |
|
−1 |
|
|
|
|
где A(q) – произвольное число, записанное в системе счисления с основанием q; ai
– цифры системы счисления; n, m – количество целых и дробных разрядов.
На практике используют сокращенную запись чисел:
A(q) = an an−1...a1a0a−1...a−m . |
(2) |
Например:
В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.
Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада).
Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь
– неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада)
Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в табл. 1.
|
|
|
|
|
Таблица 1 |
Двоичная |
Восьмеричная |
Десятичная |
Шестнадцатеричная |
||
(Основание 2) |
(Основание 8) |
(Основание |
(Основание 16) |
||
|
|
|
10) |
|
|
|
|
Триады |
|
|
Тетрады |
0 |
0 |
000 |
0 |
0 |
0000 |
1 |
1 |
001 |
1 |
1 |
0001 |
|
2 |
010 |
2 |
2 |
0010 |
|
3 |
011 |
3 |
3 |
0011 |
|
4 |
100 |
4 |
4 |
0100 |
|
5 |
101 |
5 |
5 |
0101 |
|
6 |
110 |
6 |
6 |
0110 |
|
7 |
111 |
7 |
7 |
0111 |
|
|
|
8 |
8 |
1000 |
|
|
|
9 |
9 |
1001 |
|
|
|
|
A |
1010 |
|
|
|
|
B |
1011 |
|
|
|
|
C |
1100 |
|
|
|
|
D |
1101 |
|
|
|
|
E |
1110 |
|
|
|
|
F |
1111 |
Для различения систем счисления, в которых представлены числа, в обозначение двоичных и шестнадцатеричных чисел вводят дополнительные реквизиты:
для двоичных чисел – нижний индекс справа от числа в виде цифры 2 или букв В или b (binary – двоичный), либо знак B или b справа от числа. Например, 1010002 = 101000b = 101000B = 101000B = 101000b;
для шестнадцатеричных чисел - нижний индекс справа от числа в виде числа 16 или букв H или h (hexadecimal – шестнадцатеричный), либо знак H или h
справа от числа. Например, 3AB16B = 3ABHB = 3ABh = 3ABH = 3ABh.
Для перевода чисел из одной системы счисления в другую существуют определенные правила.
Правила перевода чисел из одной системы счисления в другую
Правила перевода различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.
1. Правила перевода целых чисел из десятичной системы счисления – в
двоичную, восьмеричную и шестнадцатеричную (результатом всегда является целое число):
а) исходное целое число делится на основание системы счисления, в которую переводится (2, 8 или 16); получается частное и остаток;
б) если полученное частное не делится на основание системы счисления так, чтобы образовалась целая часть, отличная от нуля, процесс деления
прекращается, переходят к шагу в). Иначе над частным выполняют действия, описанные в шаге а);
в) все полученные остатки и последнее частное преобразуются в соответствии с табл. 1 в цифры той системы счисления, в которую выполняется перевод;
г) формируется результирующее число: его старший разряд – полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым. Таким образом, младший разряд полученного числа – первый остаток от деления, а старший – последнее частное.
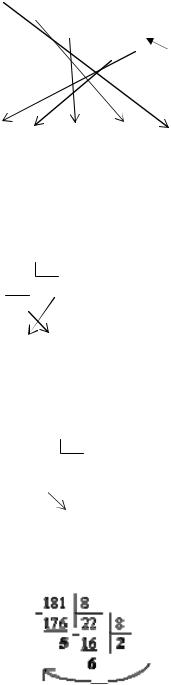
Пример 1. Выполнить перевод числа 19 в двоичную систему счисления:
_19 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
18 |
|
_9 |
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
8 |
|
_4 |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
4 |
|
|
|
|
|
2 |
|
||||
|
|
|
|
_2 |
|
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0 |
|
2 |
|
1 |
последнее частное от деления (последующее деление 1 |
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на 2 не дает отличного от нуля частного). Это старший |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разряд результирующего двоичного числа. |
1 |
|
0 |
|
|
0 |
|
1 |
|
1 – результирующее число |
||||||
Таким образом, 19 = 100112.
Пример 2. Выполнить перевод числа 19 в шестнадцатеричную систему счисления:
_19 16 16 1
3
1 3 – результирующее число.
Таким образом, 19 = 1316.
Пример 3. Выполнить перевод числа 123 в шестнадцатеричную систему счисления:
_123 16 112 7
11
7 В – результирующее число.
Таким образом, 123 = 7В16. Пример 4. Перевести 18110 →"8"с.с.

Результат 18110 = 2658 .
Пример 5. Перевести 62210 "16" с.с.
Результат: 62210 = 26E16
2. Правила перевода правильных дробей из десятичной системы счисления – в двоичную, восьмеричную и шестнадцатеричную (Результатом является всегда правильная дробь):
а) исходная дробь умножается на основание системы счисления, в которую переводится (2, 8 или 16);
б) в полученном произведении целая часть преобразуется в соответствии с табл. 1 в цифру нужной системы счисления и отбрасывается – она является старшей цифрой получаемой дроби;
в) оставшаяся дробная часть вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами а) и б).
г) процедура умножения продолжается до тех пор, пока ни будет получен нулевой результат в дробной части произведения или ни будет достигнуто требуемое количество цифр в результате;
д) формируется результат: последовательно отброшенные в шаге б) цифры составляют дробную часть результата, причем в порядке уменьшения старшинства.
Пример 6. Выполнить перевод числа 0,847 в двоичную систему счисления. Перевод выполнить до четырех значащих цифр после запятой.
Имеем:
*0,847 2
1,694  *0,694
*0,694
2
1,388  *0,388
*0,388
2
0,776  *0,776
*0,776
2
1,552 и т.д.
0,1101 – результирующее число.
В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр. Таким образом, 0,847 = 0,11012.
Пример 7. Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.
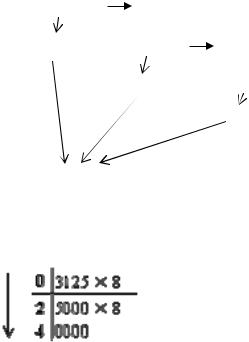
*0,847 |
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
13,552 |
|
*0,552 |
|
|
|
||
D |
|
16 |
|
|
|
||
8,832 |
*0,832 |
||||||
|
|
|
8 |
|
|
16 |
и т.д. |
|
|
|
|
13,312 |
|||
D
0,D8D – результирующее число.
В данном примере также процедура перевода прервана.
Таким образом, 0,847 = 0,D8D16. Пример 8. Перевести 0,312510 →"8"с.с.
Результат 0,312510 = 0.248
3. Правила перевода из двоичной, восьмеричной и шестнадцатеричной систем счисления – в десятичную. В этом случае рассчитывается полное значение числа по формуле (1).
Пример 9. Выполнить перевод числа 1316 в десятичную систему счисления. Имеем:
1316 = 1*161 + 3*160 = 16 + 3 = 19.
Таким образом, 1316 = 19.
Пример 10. Выполнить перевод числа 100112 в десятичную систему счисления. Имеем:
100112 = 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 16+0+0+2+1 = 19.
Таким образом, 100112 = 19.
Пример. Перевести 703.8 →"10"с.с. 703.8 =7 82 + 0 81 + 3 80 = 451.10
Пример 11. Выполнить перевод из двоичной системы счисления в десятичную числа 0,11012. Имеем:
0,11012 = 1*2-1 + 1*2-2 + 0*2-3 +1*2-4 = 0,5 + 0,25 + 0 + 0,0625 = 0,8125.
Расхождение полученного результата с исходным для получения двоичной дроби числом (см. пример 8) вызвано тем, что процедура перевода в двоичную дробь была прервана.
Таким образом, 0,11012 = 0,8125.
Пример 12. Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D16. Имеем:

0,D8D16 = 13*16-1 + 8*16-2 + 13*16-3 = 13*0,0625 + 8*0,003906 + 13* 0,000244 = 0,84692.
Расхождение полученного результата с исходным для получения двоичной дроби числом (см. пример 9) вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.
Таким образом, 0,D8D16 = 0,84692.
Пример 13. Перевести 0,416 →"10"с.с.
0,.416 = 4 16−1 =0,.2510 .
4. Правила перевода целых чисел из двоичной системы счисления в
шестнадцатеричную:
а) исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;
б) каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с табл..1.
Пример 14. Выполнить перевод числа 100112 в шестнадцатеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4 числа цифр. Имеем:
100112 = 000100112
 первая тетрада – младшая цифра числа вторая тетрада – старшая цифра числа
первая тетрада – младшая цифра числа вторая тетрада – старшая цифра числа
В соответствии с табл. 1 00112 = 316 и 00012 = 116. Тогда 100112 = 1316.
5.Правила перевода правильных дробей из двоичной системы счисления
вшестнадцатеричную:
а) исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности
4;
б) каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с табл. 1.
Пример 15. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,11012. Имеем:
0,11012 = 0,11012
 первая (и единственная) тетрада
первая (и единственная) тетрада
В соответствии с табл. 1 11012 = D16. Тогда имеем 0,11012 = 0,D16.
Пример 16. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,00101012.

Поскольку количество цифр дробной части не кратно 4, добавим справа незначащий ноль:
0,00101012 = 0,001010102.
 вторая тетрада первая тетрада
вторая тетрада первая тетрада
В соответствии с табл. 1 00102 216 и 10102 = A16. Тогда имеем 0,00101012 =
0,2A16.
6. Правила перевода целых чисел из двоичной системы счисления в
восьмеричную:
а) исходное число разбивается на триады (т.е. 3 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 3, оно дополняется слева незначащими нулями до достижения кратности 3;
б) каждая триада заменятся соответствующей восьмеричной цифрой в соответствии с табл. 1.
Пример 17. Выполнить перевод числа 100112 в восьмеричную систему счисления.
Поскольку в исходном двоичном числе количество цифр не кратно 3, дополняем его слева незначащими нулями до достижения кратности 3 числа цифр. Имеем:
100112 = 0100112

 первая триада – младшая цифра числа вторая триада – старшая цифра числа
первая триада – младшая цифра числа вторая триада – старшая цифра числа
В соответствии с табл. 1 0112 = 38 и 0102 = 18. Тогда 100112 = 238.
7.Правила перевода правильных дробей из двоичной системы счисления
ввосьмеричную:
а) исходная дробь делится на триады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 3, оно дополняется справа незначащими нулями до достижения кратности
3;
б) каждая триада заменяется шестнадцатеричной цифрой в соответствии с табл. 1.
Пример 18. Выполнить перевод из двоичной системы счисления в восьмеричную числа 0,1102. Имеем:
0,1102 = 0,1102
 первая (и единственная) триада
первая (и единственная) триада
В соответствии с табл. 1 1102 = 68. Тогда имеем 0,1102 = 0,616.
Пример 19. Выполнить перевод из двоичной системы счисления в восьмеричную числа 0,001012.
Поскольку количество цифр дробной части не кратно 3, добавим справа незначащий ноль:
0,001012 = 0,0010102.
 вторая триада
вторая триада
первая триада
В соответствии с табл.1 0012 = 18 и 0102 = 28. Тогда имеем 0,001012 = 0,128.
8. Правила перевода целых чисел из шестнадцатеричной системы счисления в двоичную:
а) каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с табл. 1. Если в таблице двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;
б) незначащие нули в результирующем числе отбрасываются.
Пример 19. Выполнить перевод числа 1316 в двоичную систему счисления.
По табл. 1. имеем: 116 = 00012; 316 = 00112. Тогда 1316 = 000100112. После удаления незначащих нулей имеем 1316 = 100112.
9. Правила перевода правильных дробей из шестнадцатеричной системы счисления в двоичную:
а) каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с табл. 1;
б) незначащие нули отбрасываются.
Пример 20. Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А16.
По таблице 1 имеем 216 = 00102 и А16 = 10102.
Тогда 0,2А16 = 0,001010102.
Отбросим в результате незначащий ноль и получим окончательный результат: 0,2А16 = 0,00101012.
9.Правила перевода целых чисел из восьмеричной системы счисления в двоичную:
а) каждая цифра исходного числа заменяется триадой двоичных цифр в соответствии с табл. 1. Если в таблице двоичное число имеет менее 3 цифр, оно дополняется слева незначащими нулями до триады;
б) незначащие нули в результирующем числе отбрасываются.
Пример 21. Выполнить перевод числа 238 в двоичную систему счисления.
По табл. 1. имеем: 28 = 0102; 38 = 0112. Тогда 238 = 0100112. После удаления незначащих нулей имеем 138 = 100112.
10.Правила перевода правильных дробей из восьмеричной системы счисления в двоичную:
а) каждая цифра исходной дроби заменяется триадой двоичных цифр в соответствии с табл. 1;
б) незначащие нули отбрасываются.
Пример 22. Выполнить перевод из восьмеричной системы счисления в
двоичную числа 0,268.
По таблице 1 имеем 28 = 0102 и 68 = 1102.
Тогда 0,268 = 0,0101102.

Отбросим в результате незначащий ноль и получим окончательный результат: 0,268 = 0,010112.
Правило перевода дробных чисел
Отдельно переводится целая часть числа, отдельно – дробная. Результаты складываются.
Пример 23. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.
Представим исходное число как сумму целого числа и правильной дроби: 19,847 = 19 + 0,847.
Как следует из примера 2, 19 = 1316; а в соответствии с примером 9 0,847 =
0,D8D16.
Тогда имеем:
19 + 0,847 = 1316 + 0,D8D16 = 13,D8D16. Таким образом, 19,847 = 13,D8D16.
Пример 24. Перевести 23,12510 →"2"с.с.
Пример 25.
а) Перевести 305,48 "2" с.с.
б) Перевести 7B2,E16 "2" с.с.
"2" с.с.
Пример 26.
а) Перевести 1101111001.11012 "8" с.с.
б) Перевести 11111111011.1001112 "16" с.с.
"16" с.с.
Перевод из восьмеричной в шестнадцатеричную систему и обратно
осуществляется через двоичную систему с помощью триад и тетрад.
Пример 27. Перевести 175.248  "16" с.с.
"16" с.с.
Результат: 175,248 = 7D,516.
Правила выполнения простейших арифметических действий
Арифметические операции для двоичных, восьмеричных и шестнадцатеричных чисел выполняются по тем же правилам, что и для десятичных чисел.
