4.7. Интегрирование уравнений Пуассона и Лапласа

В связи с тем, что любое электростатическое поле можно описать либо уравнением Пуассона, либо уравнением Лап­ласа, все задачи электростатики делятся на две большие группы.

Первая группа задач: необходимо рассчитать поле в пространстве, для которого задано распределение плотности заряда. Эта задача сводится к интегрированию уравнения Пуассона . Общий интеграл этого уравнения можно найти следующим образом. Определим потенциал в точке А (рис. 4.16), создаваемый зарядом с объемной плотностью ρ внутри элементарного объемаdv.

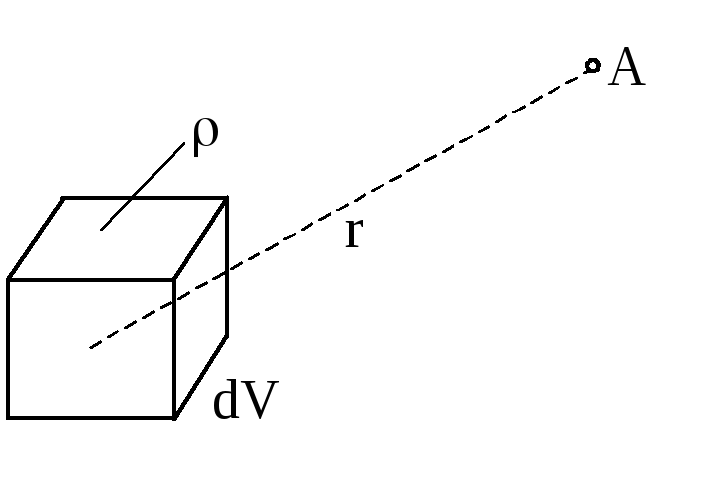
Рис. 4.16. К определению потенциала в первой группе задач электростатики

Рассматривая заряд объема dvкак точечный по отношению к точке А, на основании (4.9) можно записать

,

а после интегрирования по всему объему получим общий интеграл уравнения Пуассона

. (4.37)

Однако нужно заметить, что в большинстве случаев выполнить это интегрирование не представляется возможным.

Вторая группа задач: рассматривается некоторая область пространства и ограничивающие ее поверхности, для которых заданы граничные условия. Требуется определить поле в этой области. Очевидно, что в данном случае распределение потенциала внутри области описывается уравнением Лапласа, а решение задачи сводится к интегрированию этого уравнения при заданных граничных условиях. Эта группа задач относится к так называемым краевым задачам. Здесь различают задачу Дирихле, если задано распределение потенциала по ограничивающей поверхности (x,y,z), и задачу Неймана, если задано распределение плотности зарядов по ограничивающей поверхности. Бывают также и комбинированные задачи. Задачи называются внутренними краевыми задачами, если область ограничена, и внешними, если область является неограниченной.

Аналитическое решение этой группы задач возможно только для небольшого числа граничных условий. Большинство же задач приходится решать приближенными численными методами.

Из аналитических методов интегрирования уравнений в частных производных широко известен метод Фурье — Бернулли. Рассмотрим применение этого метода на примере определения поля цилиндра, помещенного в однородное электрическое поле.

4.8. Поле Цилиндра, помещенного в однородное электрическое поле

В однородное поле Е₀вносится диэлектрический цилиндр (рис. 4.17).

Рис. 4.17. К определению поля цилиндра, помещенного в однородное электрическое поле

Будем считать, что цилиндр бесконечно длинный, aего ось перпендикулярна линиям внешнего поля. Вблизи цилиндра поле исказится и не будет однородным, а вдали от него останется однородным. Задача заключается в определении поля вблизи цилиндра и внутри него.

При решении удобно выбрать цилиндрическую систему координат, ось zкоторой совпадает с осью цилиндра. Удобство заключается в том, что картина поля будет одинаковой в любой плоскости перпендикулярной оси цилиндра. То есть поле является плоскопараллельным.

Согласно методу Фурье — Бернулли решение ищется в виде суммы произведений трех функций, каждая из которых зависит только от одной переменной:

.

Каждое из решений удовлетворяет уравнению Лапласа, а все решение в целом – граничным условиям.

Для рассматриваемой задачи решение не должно зависеть от координаты z(поле плоскопараллельное), то есть

.

Кроме того, из условий симметрии легко видеть, что:

1) потенциал представляет периодическую функцию поВ_n()=В_n(+2), следовательно, функцию В_n() можно представить рядом Фурье;

2) ввиду того, что функция А_n(r) зависит только от радиусаr, то решениепредставляет собой ряд Фурье, коэффициенты которого зависят от координатыr;

3) для одного и того же расстояния от центра цилиндра rдолжно выполняться равенство()=(—), то есть ряд Фурье содержит только постоянную составляющую и косинусоиды. Следовательно, решение может быть записано в виде

. (4.38)

Теперь решение (4.38) подставим в уравнение Лапласа ²=0, записанное в цилиндрических координатах. Проделав необходимые выкладки, получим

.

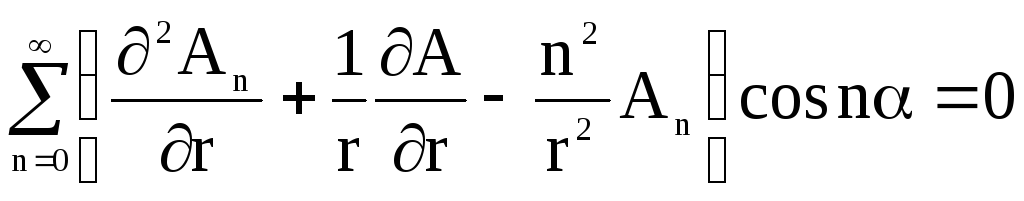Это равенство должно выполняться для произвольных nи, что возможно только при условии:

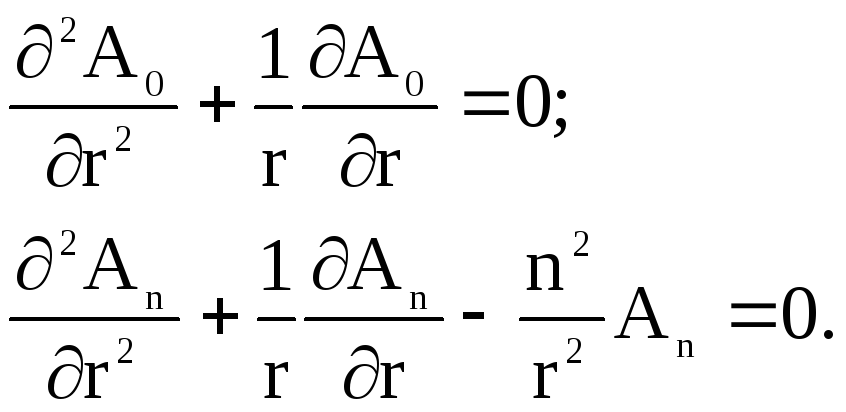
Решение этих дифференциальных уравнений известны:

(4.39)

(4.40)

Величины N_nи М_nявляются постоянными интегрирования, которые нужно определить. Для их определения используются граничные условия.

Условимся все величины, относящиеся к внутренним областям цилиндра, снабжать индексом i, а величины, относящиеся к внешним областям цилиндра,— индексом е.

Для очень удаленных от цилиндра областей возмущающее действие цилиндра уже не должно сказываться, то есть поле здесь должно быть однородным . С учетом соотношений приведенных на рис. 4.17, можно записать. Такой же результат должен получиться, если найти градиент от выражения (4.38) и записать его со знаком «минус»

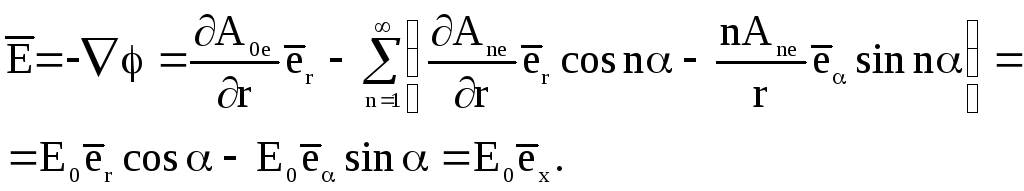
Из этого равенства получим, что для n=1 должно быть

.

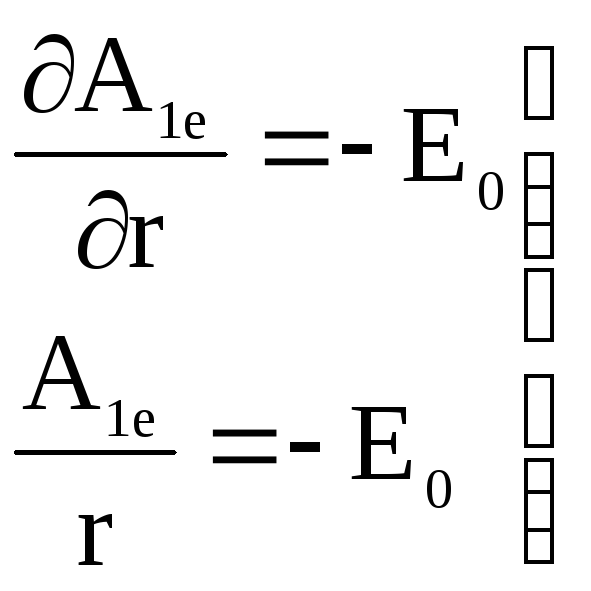Совместное решение, этой системы уравнений имеет вид A_1е(r)=-E₀r=N_1erилиN_1е=-Е₀. Относительно остальных коэффициентов, входящих в уравнения для внешней области, можно сказать следующее: коэффициенты А_ne и первые производные поrот коэффициентов А_0еи А_ne (дляn2) должны стремиться к нулю приr. Согласно этому выводу и (4.40) заключаем, чтоN_ne=0 и, следовательно,

. (4.41)

С другой стороны, как уже отмечалось выше, Е(r) = Е₀ē_х. Это дает возможность записать

(4.42)

Сравнение (4.41) при rс (4.42) показывает, чтоN_0e=0, и поэтому

(4.63)

Для внутренней области с учетом того, что потенциал в ней не должен принимать бесконечно больших значений, принимаем N_0i=0 иM_ni=0, а следовательно,

. (4.44)

Для границы раздела внутренней и внешней областей должно выполняться граничное условие _i(r=a)=_e(r=a), которое с учетом (4.43) и (4.44) дает

, (4.45)

а также граничное условие D_ni=D_neили, которое приводит к

(4.46)

Из (4.45) получаем

M_0i=M_0e=M₀. (4.67)

Для n=1 из (4.45) и (4.46) после сокращения наacosиcosимеем

.

Решая эту систему уравнений, получим:

(4.48)

. (4.49)

Для n2 уравнения (4.45) и (4.46) после сокращения наcosnдают:

N_niaⁿ=M_nea^-n;

_iN_nia^n-1=-_eM_nea^-(n+1).

Для _i>0 и_е>0 (а только эти значения и имеют физический смысл) вышеприведенная система уравнений получается несовместимой. Поэтому дляn2 остаётся принять

N_ni=M_ne=0. (4.50)

Таким образом, с учетом (4.48), (4.49), (4.50) и , полагая =0 при, что дает М₀=0, решение будет иметь вид:

; (4.51)

.

Для напряженности электрического поля во внешней области (rа) получим:

; (4.52)

Замечая, что для внутренней области

,

имеем

. (4.53)

Из этого выражения видно, что внутри цилиндра поле однородно и имеет только составляющую, совпадающую с осью х. Картины поля для i>e иi<e приведены на рис. 4.18,а, б.

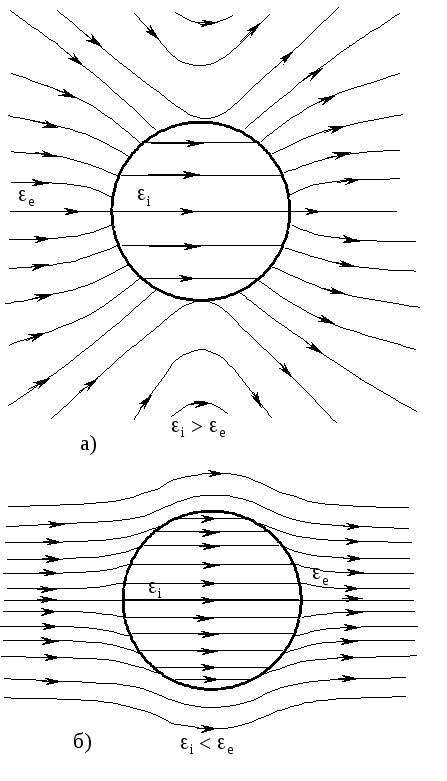
Рис. 4.18. Картины поля внутри и вне цилиндра для случаев: а - _i>_eи б -_i<_e

На основании (4.53) можно утверждать, что если в диэлектрике имеются инородные нитевидные включения, имеющие меньшую диэлектрическую проницаемость, чем окружающая среда, то величина напряженности электрического поля в таком инородном включении (при _i«_e) может в два раза (4.53) превышать напряженность поля, которая существовала бы при отсутствии неоднородности. С физической точки зрения полученный результат можно объяснить так: при поляризации на поверхности инородного включения с внешней и внутренней стороны появляются связанные заряды противоположных знаков. Причем число зарядов на внешней поверхности превышает число зарядов на внутренней (_i«_e). Эти нескомпенсированные связанные заряды и создают дополнительное поле, которое складывается с внешним полем.

Найденное решение (4.51) можно применить к задаче о проводящем цилиндре в однородном внешнем поле. Для этого нужно считать _i=При этомE_ix=0, что имеет место для проводника в условиях электростатики.