TTM_L

ЛЕКЦИИ ПО ТЕОРИИ ТЕПЛОМАССООБМЕНА

ЛЕКЦИЯ 1. Введение. Основные положения теории теплопроводности

Список лекций по теории теплообмена

ЛЕКЦИЯ 1. Введение. Основные положения теории теплопроводности.

ЛЕКЦИЯ 2. Стационарная теплопроводность в пластине и цилиндре с постоянной и переменной λ ЛЕКЦИЯ 3. Стационарная теплопроводность при наличии внутренних источников.

ЛЕКЦИЯ 4. Методы интенсификации теплопередачи. Прямой стержень постоянного сечения. ЛЕКЦИЯ 5. Теплопередача через оребренную поверхность ЛЕКЦИЯ 6. Конвективный теплообмен в однофазной среде. Факторы. Мат. модель.

ЛЕКЦИЯ 7. Основы теории подобия и моделирования процессов теплоотдачи. ЛЕКЦИЯ 8. Теплоотдача при продольном обтекании плоской поверхности ЛЕКЦИЯ 9. Теплоотдача при течении жидкости в трубах и каналах.

ЛЕКЦИЯ 10. Теплоотдача при течении жидкости в трубах и каналах (переходный режим) и при поперечном обтекании одиночной трубы и пучков труб.

ЛЕКЦИЯ 11. Теплоотдача при свободном движении жидкости ЛЕКЦИЯ 12. Специальные вопросы конвективного теплообмена в однородной среде (теплоотдача

при сверхкритическом состоянии вещества и при течении газа с большой скоростью). ЛЕКЦИЯ 13. Теплообмен при фазовых превращениях. Конденсация пара.

ЛЕКЦИЯ 14. Теплообмен при кипении однокомпонентной жидкости ЛЕКЦИЯ 15. Теплообмен излучением. Основные понятия. Виды лучистых потоков. Баланс тепло-

ты падающего излучения.

ЛЕКЦИЯ 16. Законы излучения абсолютно черных и серых тел. ЛЕКЦИЯ 17. Лучистый теплообмен произвольно расположенных тел.

ЛЕКЦИЯ 18. Зональный метод расчета лучистого теплообмена. Теплообмен в газовой среде. ЛЕКЦИЯ 19. Дифференциальные уравнения тепломассообмена и тепломассоотдачи. ЛЕКЦИЯ 20. Тройная аналогия. Тепломассоотдача при конденсации пара ЛЕКЦИЯ 21. Нестационарная теплопроводность.

ЛЕКЦИЯ 22. Нагрев цилиндра. Регулярный режим. ЛЕКЦИЯ 23. Основы расчета теплообменных аппаратов

ЛЕКЦИЯ 24. Средний температурный напор. Поверочный тепловой расчет теплообменных аппаратов.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА (имеющаяся в электронном виде)

1.Кутателадзе С. С. Основы теории теплообмена. – Новосибирск: Наука, 1970.

2.Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. – Теория тепломассообмена. М.: Энергия, 1981.

3.Лыков А. В. Теория теплопроводности. – М.: высшая школа, 1967.

4.Михеев М. А., Михеева И. М. Основы теплопередачи. – М.: Энергия, 1977.

5.Эккерт Э. Р., Дрейк Р. М. Теория тепло и массообмена. – М.: Госэнергоиздат, 1961.

Введение

Процессы переноса теплоты играют существенную роль в любом современном технологическом процессе. Этот курс посвящен изучению закономерностей процессов переноса теплоты, методов расчета и анализа этих процессов. Если в термодинамике рассматриваются закономерности преобразования энергии, то в этом курсе изучаются механизмы переноса теплоты и их особенности.

Теория теплопередачи или теплообмена – это учение о самопроизвольных необратимых процессах распространения теплоты в пространстве. Перенос теплоты осуществляется тремя основными способами.

1

Теплопроводность представляет собой молекулярный перенос теплоты в телах или между ними, обусловленный переменностью температуры в рассматриваемом пространстве. Теплопроводность в чистом виде имеет место лишь в твердых телах.

Конвекция возможна только в текучей среде. Под конвекцией теплоты понимают процесс ее переноса при перемещении объемов жидкости или газа (текучей среды) в пространстве из области с одной температурой в область с другой температурой. При этом перенос теплоты неразрывно связан с переносом самой среды. Конвекция теплоты всегда сопровождается теплопроводностью. Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. В инженерных расчетах часто определяют конвективный теплообмен между потоком текучей среды и поверхностью твердого тела. Этот процесс конвективного теплообмена называют конвективной теплоотдачей или просто теплоотдачей.

В технике и в быту часто происходят процессы теплообмена между текучими средами, разделенными твердой стенкой. Процесс передачи теплоты от горячей среды к холодной через разделяющую их стенку называется теплопередачей.

Тепловое излучение – это процесс распространения теплоты с помощью электромагнитных волн, обусловленный только температурой и оптическими свойствами излучающего тела. При этом внутренняя энергия тела (среды) переходит в энергию излучения. Процесс превращения внутренней энергии вещества в энергию излучения, переноса излучения и его поглощения веще-

ством называется тепловым излучением.

Процессы теплопроводности и конвективного теплообмена могут сопровождаться теплообменом излучением. Теплообмен, обусловленный совместным переносом теплоты излучением и теплопроводностью, называют радиационно-кондуктивным теплообменом. Если перенос теплоты осуществляется еще и конвекцией, то такой процесс называют радиационно-конвективным теплообменом. Иногда эти виды переноса теплоты называют сложным теплообменом.

Многие процессы переноса теплоты сопровождаются переносом вещества. Например, при испарении воды в воздух, помимо теплообмена, имеет место и перенос образовавшегося пара в паровоздушной смеси. Перенос пара осуществляется как молекулярным, так и конвективным путем. Совместный молекулярный и конвективный перенос массы называют конвективным мас-

сообменом.

При теоретическом исследовании теплообмена приходится вводить некоторые модельные представления о среде, в которой происходят изучаемые процессы. Рассматриваемые газы, жидкости и твердые тела в подавляющем большинстве случаев считаются сплошной средой, т. е. средой при рассмотрении которой допустимо пренебречь ее дискретным строением. Различают однородные и неоднородные сплошные среды. В первых физические свойства в разных точках одинаковы при одинаковых температуре и давлении, в неоднородных средах – различны. Различают также изотропные и анизотропные сплошные среды. В любой точке изотропной среды ее физические свойства не зависят от выбранного направления, а в анизотропной среде некоторые свойства в данной точке могут быть функцией направления.

Сплошная среда может быть однофазной и многофазной. В однофазной среде, состоящей из чистого вещества или из смеси веществ, свойства изменяются в пространстве непрерывно. В многофазной среде, состоящей из ряда однофазных частей, на границах раздела свойства изменяются скачками. Теплообмен в однофазных и многофазных системах протекает по-разному.

2

Основные положения теории теплопроводности

Явление теплопроводности связано с наличием в теле изменения температуры, т. е. с понятием температурное поле. Этим термином определяется совокупность данных о пространственно временном изменении температуры. В общем случае температурное поле является функцией t=f(x,y,z,τ), т. е. трехмерным нестационарным температурным полем. Если поле не зависит от времени τ, а только от пространственных координат x,y,z,τ, оно называется стационарным тем-

Тепловой поток (мощность передаваемой энергии) W , передаваемый теплопроводностью в

твердом теле, определяется гипотезой (законом) Фурье: «W пропорционален градиенту темпера-

туры и площади изотермической поверхности переноса F», т. е. W =-l grad t F. Коэффициент про-

порциональности l называется коэффициентом теплопроводности или теплопроводностью.

Для теплового потока через единицу площади изотермической поверхности, т. е. для плотности теплового потока получаем q =W /F = -l grad t или qx = -l ¶t/¶x, qy = -l ¶t/¶y, qz = -l ¶t/¶y.

Найдем уравнение теплопроводности, определяющее связь между изменением теплового потока в пространстве и изменением температуры во времени. Для этого выделим в твердом изотропном теле элементарный объем со сторонами dx, dy и dz. В левую грань этого объема вдоль оси x за время dτ поступает количество теплоты Qx = qx dy dz dτ, где qx - плотность теплового потока

вдоль x. С правой грани за это же время уходит Qx+dx = qx+dx dy dz dτ, где qx+dx - плотность теплового потока на координате x+dx. Разложим qx+dx в ряд Тейлора вблизи точки x, ограничиваясь двумя

членами разложения, т. е. qx+dx = qx + ¶qx/¶x dx (+¶2qx/¶x2 dx2/2!+… опускаются). Количество теплоты, аккумулированное элементом, найдем как разницу между поступившей и вышедшей теплотой:

dQx = Qx - Qx+dx = - ¶qx/¶x dx dy dz dτ = - ¶qx/¶x dv dτ, где ¶v = dx dy dz – элементарный объем. Ана-

логично для осей y и z: dQy = Qy - Qy+dy = - ¶qy/¶y dv dτ, dQz = Qz - Qz+dz = - ¶qz/¶z dv dτ. Кроме накопления теплоты в объеме могут быть внутренние источники теплоты (электрический ток, химиче-

ские реакции и т. п.) с объемной плотностью qv [Вт/м3]. В этом случае за время dτ в объеме dv выделится теплота dQv = qv dv dτ. Накопленная в объеме и выделенная внутренними источниками теплота, согласно первому закону термодинамики, идёт только на изменение её внутренней энергии (работы против внешних сил нет, т. к. элемент не деформируется), т. е. dQ = dQx+dQy+dQz+dQv = dU = c r dv dτ. Используя закон Фурье и сократив на dv, получим дифуравнение теплопроводности

где a – коэффициент теплопроводности; Ñ2 – оператор Лапласа, который в декартовой системе координат имеет вид ¶2/¶x2+¶2/¶y2+¶2/¶z2, а в цилиндрической ¶2/¶r2+(1/r) ¶/¶r+(1/r2) ¶2/¶Q2+¶2/¶t2.

Для решения конкретной задачи к этому уравнению теплопроводности надо добавить усло-

вия однозначности – геометрические условия, определяющие форму и размеры тела; физические условия, определяющие теплофизические характеристики (ТФХ); начальные условия, определяющие температурное поле при τ=0, и граничные условия (ГУ), которые подразделяются на 4 рода.

ГУ I рода. На поверхности тела задана температура tп=f(x,y,z,τ). Градиент неизвестен в отличие от ГУ II рода. Задана плотность теплового потока qп=f(x,y,z,τ). Учитывая закон Фурье, qп=-l (¶t/¶x)п. ГУ III рода. Задается в соответствии с гипотезой Ньютона: qп=a (tср-tп), где a – коэффициент теплоотдачи; tср, tп – температуры среды и поверхности. Учитывая закон Фурье, -l (¶t/¶x)п=a (tс-tп).

ГУ IV рода. Тепловой контакт: l (¶t/¶x)п1=l (¶t/¶x)п2=q, tп1-tп2=q Rт (термическое сопротивление).

3

ПРАКТИКА

Задачи

Плотность теплового потока q через неограниченную стенку или другое тело, процесс теплопроводности в котором описывается одномерным уравнением теплопроводности с граничными условиями первого рода (заданы температуры на поверхностях t1 и t2), коэффициентом теплопроводности λ, не зависящем от температуры, и протяженностью температурного поля, равной δ, описывается выражением, аналогичным математической записи закона Фурье ( q =-λ grad t), рассмотренно-

го в ЛЕКЦИИ 1, т. е. q = λ (t1 - t2) / δ. Опираясь на это выражение, решим следующие 5 задач

1.Определить плотность теплового потока через неограниченный стальной лист толщиной 0,02 м (материал – нержавеющая сталь 1Х18Н9Т с теплопроводностью 16,3 Вт/(м К)) при постоянных температурах поверхностей 250 °C и 50 °C.

Ответ: 163 кВт/м2.

2.Определить коэффициент теплопроводности мельхиора марки МНЖМц 30-0,8-1, если плотность теплового потока через плоскую стенку толщиной 0,050 м, выполненную из этого сплава, при разности температур в 4,72 °C составляет 3500 Вт/м2.

Ответ: 37,1 Вт/(м К).

3.Плотность теплового потока через пластину толщиной 25 мм, изготовленной из медноникелевого сплава с теплопроводностью 171,6 Вт/(м К), равен 6864 Вт/м2. Определить разность температур на ограничивающих поверхностях.

Ответ: 1 °C.

4.Между нагревателем (573 К) и холодильником (353 К) установлен медный (380 Вт/(м К)) стержень диаметром 16 мм и длиной 250 мм. Определить величину теплового потока, передаваемого вдоль оси стержня, если его боковая поверхность идеально теплоизолирована.

Ответ: 67,2 Вт.

5.При какой толщине теплоизоляционного материала с теплопроводностью 0,038 Вт/(м К) плотность теплового потока через него будет не больше 30 Вт/м2, если разность между температурами на его поверхностях составляет 50 градусов?

Ответ: не меньше 6,3 см.

Вопросы

1.Какие способы переноса теплоты вы знаете?

2.Что такое теплоотдача?

3.Что такое теплопередача?

4.Какие физические среды называются сплошными?

5.Сформулируйте разницу между изотропными и анизотропными сплошными средами?

6.Как выглядит уравнение нестационарной теплопроводности в трехмерном случае?

7.Как записываются граничные условия первого рода

8.Как выглядят ГУ II рода в общем случае и в случае идеальной теплоизоляции?

9.Что такое граничные условия третьего рода?

10.Граничные условия четвертого рода – как они записываются в случаях реального и идеального теплового контакта?

4

ЛЕКЦИЯ 2. Стационарная теплопроводность в пластине и цилиндре с постоянной и пере-

менной λ

НЕОГРАНИЧЕННАЯ ПЛАСТИНА. λ=const

Неограниченной пластиной (стенкой) называется тело, у которого один размер конечный, а два других бесконечно велики (намного больше первого). При этом изменение температуры в теле происходит только по координате, совпадающей с конечным размером. Для определения теплового потока, проходящего через пластину, надо найти градиент температуры, т.е. температурное по-

ле. В случае стационарной одномерной задачи без источников теплоты уравнение теплопро-

n

Для n-слойной стенки плотность теплового потока q = (tс1-tс n+1)/ ∑ (δi / λi ) .

i =1

Проанализируем теплопередачу через плоскую стенку (рис. 2.2).

В этом случае на поверхностях стенки имеет место теплоотдача к жидкостям с разными температурами (tж1 и tж2) и разной интенсивностью

теплообмена (α1 и α2). Т.е. заданы ГУ-III: α1 (tж1-tc1)=-λ dt/dx, при x=0,

α2 (tc2-tж2)=-λ dt/dx, при x=0. Общее решение то же t = C1 x + C2. Будучи подставлено в ГУ, оно дает систему уравнений с неизвестными C1 и C2

α1 (tж1-C2) = -λ C1, α2 (C1 δ + C2 - tж2) = -λ C1, решение которой дает

C1=-(tж1-tж2)/[λ (1/α1+δ/λ+1/α2)], C2=tж1-(tж1-tж2)/[α1 (1/α1+δ/λ+1/α2)].

Подставляя C1 и C2 в общее решение получим t = f(x). А, зная, что dt/dx=C1, по гипотезе Фурье получим плотность теплового потока q=(tж1-tж2)/(1/α1+δ/λ+1/α2), где 1/α – термосопротивление теплоотдачи.

Если представить плотность теплового потока в виде q=k(tж1-tж2), Рис. 2.2. Теплопередача где k – коэффициент теплопередачи, получаем k=1/(1/α1+δ/λ+1/α2).

НЕОГРАНИЧЕННЫЙ ПОЛЫЙ ЦИЛИНДР. λ=const

Найдем температурное поле в цилиндрической стенке с внутренним радиусом r1 и внешним

– r2. Будем считать, что температура меняется только вдоль нормали к боковой поверхности и остается постоянной вдоль всей боковой поверхности. Внутренние источники теплоты отсутствуют.

Уравнение (1.2) в цилиндрических координатах в этом случае будет d2t/dr2+(1/r) dt/dr=0 (2.2).

Для интегрирования (2.2) заменим dt/dr на u и разделим переменные. du/∂r+u/r=0 или du/u=-∂r/r. Интегрируя последнее равенство и потенцируя результат (ln(u)=-ln(r)+C1), имеем u=C1/r. Учитывая замену u=dt/dr и интегрируя полученное еще раз, получаем t = C1 ln(r) + C2. Постоянные интегрирования найдем из граничных условий (2.3). C1=(tс1-tс2)/ln(r1/r2), C2=tс1-(tс1-tс2) ln(r1)/ln(r1/r2).

Подставив их в t = C1 ln(r) + C2, получим t = tс1-(tс1-tс2) ln(r/r1)/ln(r2/r1).

Тепловой поток через цилиндр длинной L найдем из гипотезы Фурье с учетом выражения производной. Получим: Q = λ 2π L (tс1-tс2)/ln(r2/r1).

Найдем плотность теплового потока на внутреннем и внешнем радиусах цилиндрах. Полу-

чим q1=λ(tс1-tс2)[r1/ln(r2/r1)], q2=λ(tс1-tс2)[r2/ln(r2/r1)].

5

Т.к. r2>r1, q1>q2, т.е. с увеличением r плотность теплового потока уменьшается из-за увеличения поверхности переноса теплоты. Поэтому в расчетах теплового потока через цилиндрическую поверхность используется понятие погонной (линейной) плотности теплового потока, т.е. потока теплоты через едини-

цу длины цилиндрической поверхности: ql=QL=(tс1-tс2)/[1/(2πλ) ln(d2/d1)].

Рассмотрим теплопередачу через цилиндрическую поверхность

(рис. 2.3). Пусть в трубе с внутренним диаметром d1 течет жидкость с темпе-

ратурой tж1 и интенсивностью теплообмена α1. По внешнему диаметру d2 труба омывается жидкостью с температурой tж2 и интенсивностью теплообмена α2. Запишем поток теплоты на погонный метр трубы, идущий от одной жидкости к другой через твердую стенку: ql=α1πd1(tж1-tс1)=(tc1-

где 1/(αiπdi) – термическое сопротивление теплоотдачи цилиндрической поверхности.

Проанализируем влияние изменения внешнего диаметра трубы на ql при постоянстве других параметров. Такая задача возникает, если выбирают материал для изоляции трубопровода. Из (2.4) видно, что при увеличении d2 термическое сопротивление увеличивается, а сопротивление теплоотдачи с внешней поверхности уменьшается, что связано с увеличением площади поверхности переноса теплоты. Очевидно, что есть экстремум функции ql=f(d2). Если приравнять нулю производную знаменателя по d2 {1/(2πλd2)- 1/(α2πd22)=0}, получим значение внешнего диаметра, при котором общее термическое сопротивление ми-

нимально, d2кр=2λ/α2. Отсюда вытекает, что d2кр уменьшается с уменьшением λ и увеличением α. По-

этому, если надо выбрать материал для изоляции трубопровода с внешним диаметром d2, должно выпол-

няться условие d2³d2кр, т.е. материал изоляции должен иметь теплопроводность λиз£α2d2/2. НЕОГРАНИЧЕННАЯ ПЛАСТИНА. λ=λ0(1+βt)

Запишем гипотезу Фурье для этого случая как q=-λ0(1+βt) dt/dx. Разделим переменные q dx = -λ0(1+βt) dt и проинтегрируем по x от 0 до d, а по t от t1 до t2. Учитывая, что в стационарном состоянии q=const, получим qd=λ0[1+β(t1+t2)/2] (t1-t2) (-!). Определим теплопроводность материала при средней температуре стенки, как λ*=λ0[1+β(t1+t2)/2] и получим плотность теплового потока через стенку в виде q=(t1-t2)/(d/λ*), как в случае линейной задачи, но при среднем коэффициенте теплопроводности.

Распределение температуры в стенке получим, интегрируя q dx = -λ0(1+βt) dt по x от 0 до x, а по t от t1 до t2. Имеем квадратное уравнение t2+2t/β+2qx/(βλ0)-2t1/β- t12=0, решение которого с учетом q=(t1-

t2)/(d/λ*) имеет вид t = 1/β {(1+ βt1)2 − [(1+ βt1)2 − (1+ βt 2)2 ] x / δ −1}. Видно, что распределение температуры по толщине стенки нелинейное, поэтому и градиент температуры в стенке тоже переменный. При по-

ложительном β распределение температуры по толщине стенки имеет характер кривой, выпуклой вверх, т.е. с ростом температуры градиент температуры уменьшается.

НЕОГРАНИЧЕННЫЙ ПОЛЫЙ ЦИЛИНДР. λ=λ0(1+βt)

Для того чтобы найти тепловой поток через цилиндр, запишем гипотезу Фурье для погонной плотности теплового потока с учетом, что λ=λ0(1+βt), т.е. ql=-λ0(1+βt) 2πr dt/dr. Разделим переменные и про-

интегрируем по r от r1 до r2, а по t от t1 до t2. Получим при λ* ql=(t1-t2)/[ln(d2/d1)/(2πλ*)], что аналогично выражению, полученному раньше, но при средней теплопроводности λ*.

Для определения температурного поля цилиндра при переменной теплопроводности решим уравнение d(λ(dt/dr))/dr+(1/r)d(λt)t/dr=0. Воспользуемся подстановкой λ(dt/dr)=λ*(du/dr), (2.5)

где λ* – постоянная, а u – переменная, удовлетворяющая равенству d2u/dr2+(1/r) du/dr=0, решение которого было получено раньше в виде u = tс1-(tс1-tс2) ln(r/r1)/ln(r2/r1).

Для нахождения искомого распределения температуры проведем интегрирование (2.5) с уче-

Для определения постоянной λ* проведем интегрирование (2.5) в полном диапазоне изменения параметров. Имеем λ*=λ0[1+β(t1+ t2)/2]. Подставим полученные выражения для u и λ* в (2.6) и решим полученное квадратное уравнение. После простых преобразований получим t = 1/β

{(1 + βt1)2 − [(1 + βt1)2 − (1 + βt2)2 ] ln(r / r1) / ln(r2 / r1) − 1}, почти как t в плоской стенке при λ(t).

6

ЛЕКЦИЯ 3. Стационарная теплопроводность при наличии внутренних источников теплоты

Внутренние источники теплоты в теле имеют место при протекании электрического тока, в случае химических реакций или при условии ядерных превращений. В общем случае эти источники теплоты характеризуются объемной плотностью тепловыделения qv [Вт/м3]. Определим температурное поле тел простой формы в условиях действия внутренних источников теплоты.

НЕОГРАНИЧЕННАЯ ПЛАСТИНА ПРИ ГУ-III

Пусть задана неограниченная пластина (рис. 3.1) толщиной 2δ из материала с известной теплопроводностью. Разместим ось x нормально к поверхности пластины. Начало координат разместим в центре пластины. На поверхностях пластины происходит теплообмен со средой с постоянной температурой и заданной интенсивностью теплообмена. Для расчета температурного поля пластины надо решить уравнение

dt/dx=0 при x=0 вытекает, что C1=0, а из -λdt/dx=α(t-tж) при x=δ получаем С2=tж+qvδ/α+qvδ2/(2λ).

Тогда распределение температуры по толщине пластины имее вид t=tж+qvδ/α+qvδ2[1-(x/δ)2]/(2λ). Отсюда легко получить температуры центра и поверхности пластины, а также разницу температуры по толщине пластины.

НЕОГРАНИЧЕННЫЙ ЦИЛИНДР ПРИ ГУ-III

Определим температурное поле неограниченного сплошного цилиндра радиуса R при действии распределенных источников теплоты. Считаем, что температура среды и интенсивность теплообмена постоянны по высоте и боковой поверхности цилиндра. Тогда для определения температурного поля цилиндра надо решить уравнение d2t/dr2+(1/r) dt/dr+qv/λ=0 или эквивалентное ему

уравнение (1/r)d/dr(r dt/dr)+qv/λ=0 с ГУ третьего рода: dt/dr=0 при r=0 и -λdt/dr=α(tст-tж) при r=R. Для этого уравнение (1/r)d/dr(r dt/dr)+qv/λ=0 запишем как d/dr(r dt/dr)=-qvr/λ. Интегрирование дает

λdt/dr=α(tст-tж) при r=R.

При r=0 находим, что dt/dr=-qvr/(2λ)+C1(1/r), т.е. C1=qvr2/(4λ)=0.

При r=R с учетом того, что C1=0, dt/dr = -qvR/(2λ)+C1(1/R)=-qvR/(2λ). Подставив это в ГУ-III,

получим qvR/2=α(tст-tж) и tст=qvR/(2α)+tж.

Из t=-qvr2/(4λ)+C1lnr+C2 и tст=qvR/(2α)+tж находим tст=qvR/(2α)+tж=-qvr2/(4λ)+C2, откуда C2=tж+qvR/(2α)+qvR2/(4λ).

Подставив C1 и C2 в t=-qvr2/(4λ)+C1lnr+C2 окончательно получим t=tж+qvR/(2α)+qv(R2-r2)/(4λ). Это выражение дает возможность вычислить температуру любой точки цилиндрического

стержня. Оно показывает, что распределение температуры в круглом стержне подчиняется параболическому закону.

Из выражения для распределения температуры по радиусу при r=0 найдем температуру на оси цилиндра: t=tж+qvR/(2α)+qvR2/(4λ).

Плотность теплового потока на поверхности цилиндра с учетом того, что tст=qvR/(2α)+tж,

q=α(tст-tж)=qvR/2.

Полный тепловой поток с поверхности цилиндра Q=qF=(qvR/2)2πRl=qvπR2l. Отсюда следует, что плотность теплового потока зависит только от производительности внутренних источников и от размера внешней поверхности радиусом R, через которую проходит тепловой поток.

Сравнивая распределение температуры в пластине [t=tж+qvδ/α+qv(δ2-x2)/(2λ)] и цилиндре [t=tж+qvR/(2α)+qv(R2-r2)/(4λ)], видим, что при одинаковых условиях разница температуры по толщине пластины в два раза выше, чем по радиусу цилиндра.

7

ЛЕКЦИЯ 4. Методы интенсификации теплопередачи. Прямой стержень постоянного сечения

Когда в лекции 2 рассматривалась теплопередача через цилиндрическую поверхность, было найдено выражение для вычисления погонной плотности теплового потока (2.4). Пренебрегая сопротивлением теплопроводности, в общем случае можно записать Q=(tж1-tж2)/[1/α1F1+1/α2F2]. (4.1)

Если α1>>α2, то для существенного увеличения теплового потока надо увеличивать интенсивность теплообмена со стороны теплоносителя, что не всегда возможно, или увеличить поверхность переноса теплоты. Практически такое увеличение поверхности осуществляется с помощью различных ребер, стержней или шипов. Объединяет эти элементы одна общая черта: в них можно пренебречь изменением температуры по толщине тела и рассматривать изменения температуры только вдоль его оси. На поверхности тела имеет место теплообмен со средой постоянной температуры, причем интенсивность этого процессу тоже можно считать постоянной. Таким образом, в теле типа ребра или стержня перенос теплоты вдоль его оси осуществляется теплопроводностью, а с его поверхности – теплоотдачей в среду.

Имеется большое число типов ребер. Наиболее распространенные среди них – прямые ребра постоянного и переменного сечения на плоской поверхности или по образующей цилиндрической поверхности, кольцевые и спиральные ребра на цилиндрической поверхности, килевые и т.п.

Уменьшение теплового потока вдоль оси x связано с отводом теплоты с поверхности стержня в среду. dQx=Qx-Qx+dx=λ f d2t/dx2 dx=α (t-tж) u dx.

Переходя к превышению температуры стержня над температурой среды ϑ=t-tж, получим d2ϑ/dx2=m2ϑ, где m= αu /(λf ) – характеристика стержня, представляющая собой меру отношения потоков теплоты теплоотдачей с поверхности стержня и теплопроводностью вдоль его оси. Общее решение этого дифференциального уравнения будет ϑ(x)=Ae-mx+Bemx=A ch(mx)+B sh(mx). (4.3)

Для определения постоянных интегрирования A и B надо к основному диф. уравнению добавить условия на границах стержня. В месте контакта стержня с поверхностью (при x=0) чаще всего известна температура t0. Рассмотрим несколько отдельных задач в зависимости от условий на другом конце стержня.

Задача 1. Бесконечно длинный стержень

ГУ имеют вид: ϑ=t0-tж=ϑ0 при x=0; ϑ=0 при x=∞.

Используя (4.3), из последнего ГУ получим B=0. Тогда из ГУ для x=0 получим A=ϑ0. Окончательное решение имеет вид: ϑ(x) = ϑ0 Ae-mx.

или как тепловой поток, поступающий в стержень при x=0, т.е. Q=-λ f (dϑ/dx)x=0=ϑ0 αuλf . Как и ожидалось, полученные результаты одинаковы.

8

Задача 2. Стержень конечной длины без теплообмена на торце

Рассмотрим стержень длинной h, в основании которого задана температура t0, а на свободном торце теплообмен отсутствует, т.е. он закрыт адиабатной оболочкой.

ГУ в этом случае имеют вид: ϑ=t0-tж=ϑ0 при x=0; dϑ/dx=0 при x=h.

Используем второй вид общего решения (4.3). Тогда по условию при x=0 получим A=ϑ0. Для определения другой постоянной продифференцируем общее решение в соответствии с условием идеальной теплоизоляции при x=h. Тогда ϑ0m sh(mh)+B m сh(mh)=0, откуда B=-ϑ0 sh(mh)/сh(mh), а распределение температуры ϑ(x) = ϑ0 сh(m (h-x))/сh(mh).

Тепловой поток, передаваемый стержнем в окружающую среду, равен потоку, поступившему в основание стержня Q=-λ f (dϑ/dx)x=0=ϑ0 αuλf th(mh).

Задача 3. Стержень конечной длины с теплообменом на торце

Задан стержень длинной h, в основании которого задана температура t0, а на свободном торце происходит теплообмен со средой с постоянной температурой, т.е. ГУ III рода. Тогда ϑ=t0-tж=ϑ0

при x=0; -λ dϑ/dx = α1 ϑ при x=h.

Используем второй вид общего решения (4.3). Тогда по условию при x=0 получим A=ϑ0. Для определения другой постоянной продифференцируем общее решение, результат подставим в ус-

ловие при x=h, введя N=α1/(λm). Получаем: -[ϑ0 sh(mh)+B сh(mh)] = N [ϑ0 ch(mh)+B sh(mh)], от-

куда после простых преобразований находим B и распределение температуры по стержню ϑ(x) = ϑ0 [сh(m(h-x))+N sh(m(h-x))]/[сh(mh)+N sh(mh)] Легко видеть, что при α1=0 (отсутствии теплообмена на торце) это решение совпадает с ϑ(x) = ϑ0 сh(m (h-x))/сh(mh), полученным для предыдущего случая.

Тепловой поток, передаваемый стержнем, найдем, как в предыдущем случае,

Q=-λ f (dϑ/dx)x=0=ϑ0 αuλf [th(mh)+N]/[1 + N th(mh)].

Задача 4. Стержень с разными температурами на концах

Задан стержень длинной h, на одном конце которого задана температура t1, а на другом – температура t2.

Граничные условия запишем в виде:

ϑ=ϑ1 при x=0; ϑ=ϑ2 при x=h.

Используем второй вид общего решения (4.3). Тогда из условия при x=0 получим A=ϑ1. Из условия при x=h имеем B=[ϑ2 - ϑ1 сh(mh)]/sh(mh).

Если подставить полученные постоянные в общее решение, после простых преобразований найдем распределение температуры по стержню

ϑ(x) = [ϑ1 sh(m(h-x)) + ϑ2 sh(mx))]/sh(mh).

Тепловой поток, передаваемый стержнем, найдем как

h

Q= ∫ αuϑ(x)dx =(ϑ1+ϑ2 αuλf [ch(mh)-1]/sh(mh).

0

9

ЛЕКЦИЯ 5. Теплопередача через оребренную поверхность {Q=(tж1-tж2)/[1/α1F1+1/α2F2]. (4.1)}

Рассмотрим немного подробнее (4.1) и предположим, что α1>>α2 и со стороны меньшей интенсивности теплообмена поверхность теплообмена состоит из ребер (F2р) и межреберной поверхности (F2г), т. е. F2 = F2р + F2г. Будем считать, что интенсивность теплообмена с поверхности ребер и между ними одинаковая В этом случае тепловой поток, передаваемый с оребренной поверхности в среду, может быть записан в виде: Q=α2[F2г(t2-tж2)+F2р(t*-tж2)], где t*- средняя температура ребра. В связи с тем, что F2р>>F2г, с достаточной точностью это выражение можно заменить на

а) Q=α2[0+F2р(t*-tж2)]=α2F2р(t*-tж2)= α2F2р(t2-tж2)(t*-tж2)/(t2-tж2). С другой стороны, тепловой поток на поверхности F1 можно записать по закону Ньютона б) Q=α1F1(tж1-t1)α1F1(tж1-t2), где t2– температура стенки, одинаковая как со стороны первого, так и второго теплоносителя, т. к. термическим сопротивлением теплопроводности пренебрегаем. Если в а) и б) выделить частные температурные напоры и суммировать их, можно после некоторых преобразований получить

Q=F1(tж1-tж2)/[1/α1+1/(α2ϕη)], где ϕ – F2/F1 – коэффициент оребрения; η – ( t*-tж2)/(t2-tж2) – эффективность ребра, т. е. отношение теплового потока, передаваемого ребром, к потоку, который ребро

было бы способно передать, если бы температура ребра была постоянна по высоте и равнялась температуре в основании.

Рассмотрим прямое ребро постоянного профиля, наиболее часто встречающийся на практике тип ребра.

Задано прямое ребро (рис. 2.7) высотой h, длиной L, толщиной 2δ. Расположим ось x вдоль высоты ребра. Площадь поперечного сечения ребра f=2Lδ, а периметр u=2L+2δ. Учитывая,

что L>>2δ, запишем характеристику ребра m= αu /(λf )

α2L /(λ2Lδ) = α /(λδ) .

Тепловой поток, который рассеивается ребром, пренебрегая теплообменом ребра и учитывая значения f и u, получим из выражения для потока в стержне конечной длины без теплообмена

на торце (лекция 5, задача 2) Q=-λ f (dϑ/dx)x=0=ϑ0 αuλf th(mh)=

2ϑ0L αλδ th(mh). Максимальный тепловой поток с поверхности ребра при постоянной темпера-

туре, равной температуре основания, будет Qmax=2αϑ0Lh, а эффективность ребра η= th(mh)/(mh). Используя выражение в конце задачи 3 лекции 4, можно вычислить тепловой поток с учетом теп-

лообмена торца ребра Q=-λ f (dϑ/dx)x=0=ϑ0 αuλf [th(mh)+N]/[1 + N th(mh)]. Можно также приблизительно учесть тепловой поток с торца ребра, используя полученное выше выражение Q =

2ϑ0L αλδ th(mh) и приведенную высоту ребра h0=h+δ.

Тепловой поток с погонного метра ребра из Q = 2ϑ0L 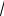αλδ th(mh) можно записать как ql = 2ϑ0 αλδ th(mh).

Анализ последнего выражения показывает, что тепловой поток является функцией двух переменных h и δ,которые, в свою очередь, определяют площадь продольного сечения ребра. Поэтому возникает вопрос про оптимальные размеры ребра заданной массы (площади продольного сечения), т. е. ребра, которое передает максимальное количество теплоты.

Пусть F=2hδ=const. Меняя в ql=2ϑ0 αλδ th(mh) параметр h, согласно выражению h=F/(2δ),

имеем ql=2ϑ0th(mF/(2δ))=f(δ).

трансцендентное уравнение относительно k: 6k=sh(2k), численное решение которого дает опти-

мальное значение kопт=1,4192. Тогда из k=F/(2δ) αλδ отыскивается оптимальная полутолщина ребра δопт=(F2α/(4k2опт λ)1/3, а также оптимальная высота ребра hопт=F/(2δопт).

Тепловой поток с погонного метра ребра оптимальных размеров: qопт=2ϑ0 αλδ опт th(kопт).

10