caplin_nikulin_modelirovanie_v_metallurgii

шения (5.23) образуют для всех узловых точек k-го слоя систему линейных алгебраических уравнений вида (5.22).

В рассмотренных схемах производная по времени аппроксимировалась односторонней разностью с использованием двух слоев сетки по времени. Такие схемы называются двухслойными.

Явная схема Дюфора – Франкеля

Полученное соотношение дает необычную для явных схем абсолютную устойчивость счета при любых шагах сетки hx и hτ . Однако следует отметить, что при больших шагах по времени рассматриваемая схема приводит к колебаниям, хотя и не возрастающим. Причиной этого являются ошибки аппроксимации. Поэтому при больших шагах по времени метод Дюфора – Франкеля неточен.

Существуют и другие явные и неявные методы разностной аппроксимации уравнения переноса.

172

5.3. Анализ ошибок

Ошибки, связанные с дискретным представлением уравнения переноса и проведением расчетов на компьютере, можно разделить на три вида: ошибки округления, ошибки аппроксимации, схемные ошибки.

Ошибки округления

Ошибки округления связаны с выполнением арифметических операций, в котором числа представляются в экспоненциальной форме с ограниченным числом разрядов. Ошибки округления можно уменьшить, изменяя метод решения матричных уравнений, последовательность арифметических операций и увеличивая число разрядов для записи чисел в компьютере (например, применяя двойную точность).

Ошибки аппроксимации

Ошибки аппроксимации обычно больше ошибок округления и связаны с дискретным представлением отдельных членов уравнения переноса, использованием разложения функции в укороченный ряд Тейлора. Порядок ошибки аппроксимации оценивается максимальным значением остаточного члена ряда Тейлора. Грубо ошибки аппроксимации можно оценить на следующем примере. При числе разбиений по толщине слоя N = = 10 шаг сетки hx ≈ 1/10, ошибка аппроксимации первой производной односторонними разностями равна О(hx) ≈ 1/10 ≈ 10 %,

второй производной – O (hx2 ) ≈ 1100≈ 1 % . Более точно ошибки

аппроксимации всего уравнения переноса можно оценить, находя решение на последовательности сгущающихся сеток.

На практике полезно строить график изменения функции в характерной точке при сгущении сетки. При этом схемы первого порядка точности в области достаточно густой сетки дают линейное приближение к точному решению, а схемы второго порядка точности – параболическое (рис. 5.6).

173

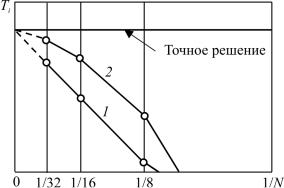
Рис. 5.6. Стремление численных решений к точному решению со сгущением сетки при схемах аппроксимации первого (1) и второго (2) порядков точности

Общим свойством ошибок аппроксимации является их исчезновение при асимптотическом стремлении к нулю шагов сетки (сгущении сетки).

Схемная ошибка консервативности

Схемные ошибки связаны со схемой конечно-разностного аналога всего уравнения переноса. В отличие от ошибок аппроксимации схемные ошибки не исчезают при асимптотическом уменьшении шагов сетки. Однако для уменьшения или исключения схемных ошибок совсем не обязательно устремлять к нулю шаги сеток.

Примером схемной ошибки является ошибка, связанная с нарушением свойства консервативности (закона сохранения) в конечно-разностном аналоге уравнения переноса энергии только конвекцией:

Явная схема аппроксимации этого уравнения имеет вид:

174

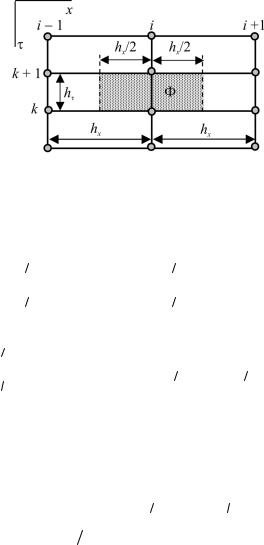
Получим это соотношение интегральным методом, интегрируя уравнение переноса по времени от τ до τ +hτ и по пространственной области Ф от x–h x/2 до x+hx/2 (рис. 5.7).

Рис. 5.7. Область интегрирования

Поскольку порядок интегрирования по времени и координате несущественен, выберем его так, чтобы можно было провести одно точное интегрирование, а именно:

Проинтегрируем выражения в квадратных скобках

Остальные интегралы можно определить численно, используя теорему о среднем, взяв за средние значения центральную точку x области интегрирования Ф и нижний предел τ времени интегрирования. В итоге получим:

Производные ∂ T ∂ x можно найти, используя формулы односторонних разностей:

175

Указанное отличие, как видно из сравнения (5.32) с соответствующей аппроксимацией конвективного члена уравнения (5.27), составляет ∆ u Ti hx и исчезает, когда ∆ u= 0 , т.е. при

постоянной скорости. Это свидетельствует о том, что интегральный и дифференциальный методы дают различные ко- нечно-разностные аналоги дифференциального уравнения переноса, причем это различие увеличивается с возрастанием градиента скорости переноса. Интегральный метод позволил учесть закон сохранения в дискретном аналоге уравнения пе-

в дискретном аналоге уравнения переноса, полученном дифференциальным методом.

Заметим, что указанная схемная ошибка в отличие от ошибок аппроксимации при сгущении сетки (hx → 0) не только не

стремится к нулю, но даже возрастает.

Другая схемная ошибка связана с неодинаковой точностью конечно-разностного представления отдельных членов уравнения переноса. Поясним ее на следующем примере. Запишем стационарное уравнение переноса энергии:

Получим конечно-разностный аналог этого уравнения, применяя для аппроксимации правой части (диффузионного члена) формулу второго порядка точности, а для левой части (конвективного члена) – формулу правосторонней разности первого порядка точности:

Уравнение (5.34) имеет низший, первый порядок точности, поэтому погрешностью O (hx2 ) , имеющей более высокий вто-

рой порядок, можно пренебречь. Подставляя в (5.34) погрешность O (hx ) из (5.5), получим:

Усредним скорость в пределах шага сетки u = u и объединим коэффициенты при вторых производных, в результате получим:

Из последнего уравнения видно, что погрешность влияет на коэффициент при диффузионном члене уравнения переноса,

поэтому ее называют схемной искусственной температуропроводностью (диффузией). Вынесем в уравнении (5.36) тем-

пературопроводность за скобку:

Введем сеточное число Пекле по локальной скорости и характерной длине, равной шагу сетки:

178

Тогда при переносе тепла получаем схемную температу-

ропроводность:

Так как коэффициент а не может быть отрицательными, то

1 − Peh > 0 , откуда

2

Последнее соотношение является условием, при котором счетная температуропроводность не проявляется. Это соотношение накладывает ограничение на шаг сетки:

2a

hx < . (5.40)

u

Однако в практических расчетах ограничение (5.40) оказывается очень жестким, поэтому диффузия, которую мы будем в дальнейшем называть счетной диффузией, всегда присутствует. С математической точки зрения счетная диффузия увеличивает физическую температуропроводность:

где счетное значение температуропроводности

Счетная диффузия проявляется в «размазывании» внешних возмущений, в стремлении сделать распределение переносимых величин более однородным.

179

Отметим, что аппроксимация всех членов уравнения переноса с одинаковым порядком точности, например вторым, приводит к исключению счетной диффузии, такие схемы называют

бездиффузионными.

Схемная ошибка транспортивности

Схемная ошибка транспортивности приводит к тому, внешнее возмущение переносится за счет конвекции не только в направлении, но и против скорости потока. Проиллюстрируем её на уравнении переноса, учитывая в нем только нестационарный и конвективный члены:

с помощью формул правосторонней и центральной разностей:

Рассмотрим некоторое возмущение Т = δ только в одной точке i = n, полагая u > 0. Тогда в точке i = n+1 по потоку

Таким образом, возмущение δ , которое должно переноситься только в направлении скорости, т.е. по потоку, при использовании формулы центральной разности для конвективного члена переносится и против потока. Схема (5.44) не обладает, поэтому, свойством транспортивности, а (5.46) характеризует схемную ошибку в точке i = n − 1, связанную с нарушением этого свойст-

180