Безруков А.В. ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

следовательно, и его достаточно определить при k=0,1,…,N/2-1, а затем, изменив знак, повторить при k=N/2, N/2+1,…,N-1.

Свойства (8.29)÷(8.30) позволяет представить ДПФ (8.28) в виде:

Из сопоставления ДПФ (8.28) и (8.32) ясно, что в (8.32) расчѐт упрощается за счѐт распараллеливания вычислений при k=0,1,…,N/2-1 и k=N/2, N/2+1,…,N- 1 по верхней и нижней формулам соответственно.

Предположим теперь, что алгоритм состоит из двух этапов разбиения ν-го и (ν-1)-го N – точечной последовательности (см. рис. 8.3):

а) сначала N – точечная последовательность разбивается на две N/2 –

точечные (8.21) и (8.22);

б) N/2 – точечная последовательность разбивается на две N/4 – точечные:

четных [x(0), x(4), …,x(N-4)] отсчѐтов; нечетных [x(2), x(6), …,x(N-2)] отсчѐтов;

в) N/2 – точечная последовательность нечѐтных отсчѐтов (8.22)-на две N/4 – точечные:

четных [x(1), x(5), …,x(N-3)] отсчѐтов; нечетных [x(3), x(7), …,x(N-1)] отсчѐтов;

г) начальная расстановка отсчѐтов производится по правилу:

а именно:

x(0), x(4), …,x(N-4), x(2), x(6), …,x(N-2): x(1), x(5), …,x(N-3), x(3), x(7), …,x(N-1).

На (ν-1)-м этапе определяются два N/2 – точечных ДПФ, причѐм каждое из них – как комбинация двух N/4 – точечных ДПФ:

- N/2 – точечное ДПФ X 0 1 (k) - как комбинация N/4 – точечных ДПФ: чѐтного X 0 2 (k ) и нечѐтного X1 2 (k) ;

- N/2 – точечное ДПФ X1 1 (k) - как комбинация N/4 – точечных ДПФ: чѐтного X 2 2 (k) и нечѐтного X 3 2 (k) .

N/2 – точечные ДПФ X 0 1 (k) и X1 1 (k) определяются по формуле (8.23),

в которой индекс ν уменьшается на единицу

ν→ν-1,

а размерности ДПФ и поворачивающего множителя понижаются вдвое

71

где L – номер этапа; m – номер ДПФ;

k – номер отсчѐта ДПФ;

M – количество L-точечных ДПФ;

Согласно (8.35), L – точечное дискретное преобразование Фурье определяется параллельно:

-первая половина отсчѐтов – по верхней формуле;

-вторая половина отсчѐтов – по нижней формуле.

Обратимся теперь к особенностям первого этапа алгоритма (i=1). По формуле (8.37) определим размерность ДПФ:

L 21 2

73

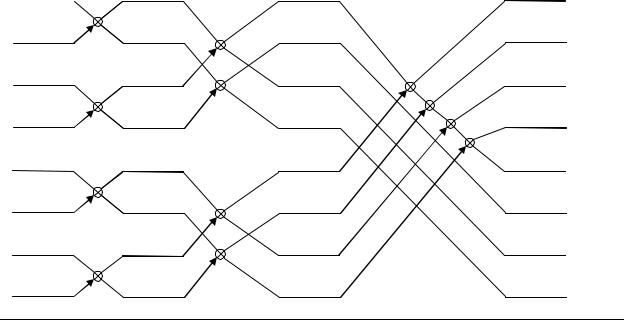
Рис. 8.4 Идея алгоритма БРФ с прореживанием по времени. По формуле (8.36) – количество 2 – точечных ДПФ

M2 i 2 1 N2 .

Сучѐтом этого перепишем общую формулу ДПФ (8.35) в виде:

где поворачивающий множитель W20 1 сохранѐн для единообразия с общей формулой (8.35).

нулевого этапа (i=0), однако такого этапа нет, поэтому для вычисления 2-х точечных ДПФ по общей формуле (8.35) перед выполнением первого этапа задаются начальные условия: каждой пары отсчѐтов прореженной последовательности – четного и нечѐтного:

точечной последовательности, полученные в результате ν-кратного разбиения исходной N-точечной последовательности (см. рис. 8.3 и 8.4)

Подставляя (8.39) в (8.38) при m=0,1,…,(N/2-1), получим N/2 формул

типа:

………………

Таким образом, общая формула (8.35) описывает алгоритм быстрого выполнения ДПФ (алгоритм БПФ с прореживанием по времени) – ν-этапную процедуру типа «цикл в цикле», где:

-внешний цикл формируется по переменной i: i=1,2,…,ν;

-первый внутренний цикл (при фиксированном i) – переменной m: m=0,1,…,M-1;

-второй внутренний цикл (при фиксированном m и i) – по переменной

k:k=0,1,…,(L/2-1). В цикле вычисляется k-й отсчѐт L – точечного ДПФ по формуле (8.35).

На выходе алгоритма согласно формуле (8.35) получим N – точечное ДПФ, отсчѐты которого следуют в естественном порядке: k=0,1,…,(N-1). Структурная схема алгоритма БПФ с прореживанием по времени на рисунке

(8.5)

75

Основной операцией алгоритма БПФ, называемой базовой, является одновременное (параллельное) вычисление двух отсчѐтов ДПФ – k-го и (k+L/2)-го по двум верхним формулам (8.35). На рисунке (8.6) приведѐн направленный граф базовой операции, получивший название «бабочка» по ассоциации с изображением графа. Кружок обозначает арифметическую операцию сложение (вычитание), верхний выход соответствует сумме, а нижний – разности; стрелка обозначает умножение на поворачивающий множитель, стоящий над ней.

Рисунок 8.6

Важно отметить, что количество «бабочек», т.е. базовых операций алгоритма, на любом i-м этапе одинаково. Действительно, согласно (8.35), на i-м этапе при фиксированном значении m и k=0,1,…,L/2 требуется L/2 «бабочек», следовательно, при m=0,1,…,(M-1) будем иметь ML/2 «бабочек». Тогда в соответствии с (8.36) и (8.37) получим одинаковое количество «бабочек» на каждом i-м этапе.

8.4.2 Пример вычисления 8-точечного БПФ

Для лучшего понимания алгоритма БПФ с прореживанием по времени рассмотрим его на примере вычисления 8-точечного ДПФ.

n 0

где N 2 23 8 , ν=3.

Алгоритм БПФ представляет собой трѐхэтапную процедуру определения ДПФ по общей формуле (8.35) при i=1,2,3.

Начальные условия алгоритма формируются в результате трѐхкратного разбиения исходной 8-точечной последовательности на чѐтные и нечѐтные отсчѐты, а именно:

-первый раз 8-точечная последовательность разбивается на две четырѐхточечные:

четных [x(0), x(2), x(4), x(6)] отсчѐтов; нечетных [x(1), x(3), x(5), x(7)] отсчѐтов;

-второй раз каждая 4-точечная последовательность вновь разбивается на две 2-х точечные: чѐтных и нечѐтных отсчѐтов по порядку их следования, начиная от нуля, а именно.

76

4-точечная последовательность [x(0), x(2), x(4), x(6)] разбивая на две 2- х точечные

четных [x(0), x(4)] отсчѐтов; нечетных [x(2), x(6)] отсчѐтов;

4-точечная последовательность [x(1), x(3), x(5), x(7)] разбивая на две 2- х точечные

четных [x(1), x(5)] отсчѐтов; нечетных [x(3), x(7)] отсчѐтов;

- третий раз каждая из 2-точечных последовательностей вновь разбирается на два отсчѐта – чѐтный и нечѐтный

2-х точечная последовательность [x(0), x(4)] на 2 отсчѐта: чѐтный x(0) и нечѐтный x(4);

2-х точечная последовательность [x(2), x(6)] на 2 отсчѐта: чѐтный x(2) и нечѐтный x(6);

2-х точечная последовательность [x(1), x(5)] на 2 отсчѐта: чѐтный x(1) и нечѐтный x(5);

2-х точечная последовательность [x(3), x(7)] на 2 отсчѐта: чѐтный x(3) и нечѐтный x(7).

Таким образом, получаем начальную расстановку отсчѐтов – прореженную последовательность

нечѐтного отсчѐтов прореженной 8-точечной последовательности (рис. 8.6)

начальные условия

Рис. 8.6 Граф алгоритма 8-точечного БПФ

77

исходной N-точечной последовательности должны быть расставлены в битреверсивном порядке своих двоичных номеров.

Таблица 8.1 Расстановка 8-точечной последовательности в бит-реверсивном порядке

8.4.4 Алгоритм БПФ с прореживанием по частоте

Формулы прямого и обратного преобразования Фурье (8.11) и (8.12) отличаются только знаком в показателе экспоненты и множителем перед суммой. Поэтому можно получить ещѐ один вариант алгоритма БПФ, выполнив преобразования, показанные на рис. 8.6 в обратном порядке. Этот способ вычисления называется алгоритм БПФ с прореживанием по частоте.

Основная идея алгоритма заключается в поэтапном вычислении N- точечного ДПФ (8.20) на ν-этапах, на каждом из которых БПФ определяется через ДПФ вдвое большей размерности. Алгоритм БПФ с прореживанием по частоте можно записать следующим образом:

а) задание начальных условий, а именно: N-точечная последовательность не прореживается, сохраняется естественный порядок следования отсчѐтов n=0,1,…,N-1;

б) на первом этапе определяется N/2-точечная ДПФ N/2-точечных последовательностей (двух половин исходной последовательности);

в) на втором этапе определяется N/4-точечная ДПФ как комбинация N/2-точечных ДПФ;

г) на i-ом этапе определяется 2i 1 -точечная ДПФ как комбинация 2i - точечных ДПФ;

д) на ν-ом этапе определяется 2-точечные ДПФ как комбинация 4- точечных ДПФ. Последовательность из N/2 2-точечных БПФ представляет собой искомое N-точечное ДПФ, отсчѐты ДПФ следуют в бит-реверсивном порядке двоичных номеров.

Идея алгоритма БПФ с прореживанием по частоте показана на рисунке

8.7

79