Вопросы для самоконтроля:

1) Сформулируйте понятия класса, группы и единичного физического явления.

2) Что включают в себя условия однозначности?

3) Что понимается под геометрическими свойствами системы?

4) Что понимается под физическими свойствами системы?

5) Что включают в себя краевые условия, и как они задаются?

6) Определите понятие сходственных точек подобных процессов.

7) Что характеризует число гомохронности Ho и в каких задачах оно используется?

8) Как формулируется основная теорема теории подобия?

9) Что утверждает -теорема?

10) Назовите физический смысл критериев подобия Эйлера Eu, Фруда Fr, Рейнольдса Re.

11) Приведите примеры безразмерных аргументов, безразмерных искомых функций и безразмерных параметры.

12) Что такое определяющие и определяемые критерии?

13) Сформулируйте основное правило моделирования.

14) В каких случаях имеет смысл использовать метод размерностей?

15) Поясните суть алгебраического метода Рэлея.

16) Назовите условия полного подобия модели образцу.

17) Что такое приближенное моделирование и в каких случаях его выполняют?

18) Что такое явление автомодельности и как оно может быть полезно?

19) Поясните суть метода локального моделирования процессов теплопередачи.

20) Что такое моделирование по аналогии?

Выводы по главе

В данной главе рассмотрены основные понятия теории подобия, такие, как класс и группа физических явлений, единичное явление, условия однозначности, включающие в себя геометрические и физические свойства системы, и краевые условия.

На примере уравнений, описывающих движение вязкой жидкости, сформулированы понятия сходственных точек, получены критерии подобия Ho, Re, Fr, Eu и установлен их физический смысл. Сформулирована основная теорема теории подобия, дано определение определяющих и определяемых критериев подобия.

Сформулировано понятие автомодельности. На конкретном примере рассмотрено, как работает метод размерностей для получения безразмерных критериев подобия. Установлено основное правило моделирования и перечислены условия полного подобия модели образцу.

Рассмотрены методы приближенного моделирования, использующие явление автомодельности, локальное тепловое моделирование и моделирование по аналогии.

Список литературы по теме

1. Гухман А.А. Применение теории подобия к исследованию процессов тепло – массообмена / А.А. Гухман. – Изд. 2-е перераб. и доп. М., «Высшая школа», 1974.  328 с.

2. Гухман А.А. Введение в теорию подобия / А.А. Гухман. – М.: Высшая школа, 1961.  140 с.

3. Гухман А.А. Применение теории подобия к исследованию процессов тепло- и массообмена / А.А. Гухман. – М.: Высшая школа, 1967.  86 с.

4. Исаченко В.П. Теплопередача: Учебник для вузов / В.П. Исаченко, В.А. Осипова, А.С. Сукомел. – 4-е изд., перераб. и доп. – М.: Энергоиздат, 1981. – 416 с.

5. Кутателадзе С.С. Основы теории теплообмена. – Изд. 5-е перераб. и доп. – М.: Атомиздат, 1979. – 416 с.

2. Физическое моделирование процессов теплопроводности

В данном разделе рассмотрено математическое описание процессов стационарной и нестационарной теплопроводности, уравнения подобия для процессов теплопроводности, охлаждение (нагревание) тела в условиях конвективного теплообмена и в условиях теплообмена излучением, моделирование процессов теплопроводности.

2.1 Математическое описание процессов теплопроводности

Процессы теплопроводности в настоящее время успешно изучаются на основе математического моделирования, однако, в некоторых случаях, например, при сложной геометрической форме твердого тела прибегают к физическому моделированию.

При исследовании теплопроводности нужно определить температурное поле внутри твердого тела при заданных начальных и граничных условиях. Рассмотрим следующие задачи:

1. перенос теплоты в твердом теле от горячей к холодной поверхности в условиях стационарной теплопроводности;

2. охлаждение (нагрев) твердого тела в окружающей среде с постоянной температурой.

Нестационарное температурное поле в твердом теле без внутренних источников теплоты в декартовой системе координат описывается дифференциальным уравнением теплопроводности:

, (2.1)

где t = t(x,y,z,) – температурное поле; x, y, z – декартовы координаты;  – время; а – коэффициент температуропроводности, м²/с:

, (2.2)

где   коэффициент теплопроводности, Вт/(мК); с  массовая теплоемкость, Дж/(кгК);   плотность тела, кг/м³. Так как величины , с,  обычно в той или иной степени зависят от температуры, то введение коэффициента температуропроводности а по выражению (2.2) оправдано лишь при незначительном изменении , с,  с температурой.

Начальное условие для уравнения (2.1) записывается так:

(2.3)

где t₀(x,y,z) – распределение температуры в начальный момент времени.

При физическом моделировании обычно полагают t₀ = const, поскольку иначе сложно обеспечить подобие температурных полей у образца и модели в начальный момент времени.

Твердое тело обычно имеет поверхности, обменивающиеся теплом с окружающей средой, или адиабатные поверхности.

На адиабатной поверхности теплообмен отсутствует, что записывается так:

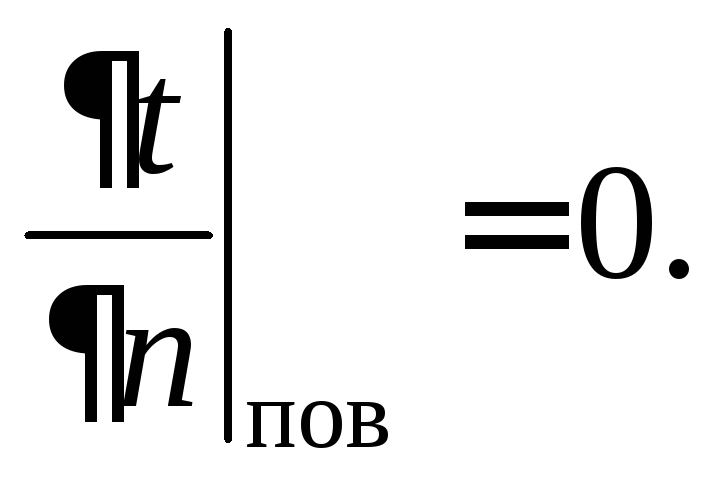(2.4)

где n – координата нормали к поверхности тела, направленная в окружающую среду; «пов» – индекс, указывающий на то, что величина относится к поверхности тела;

Конвективный теплообмен поверхности тела с жидкостью или газом описывается законом Ньютона-Рихмана:

(2.5)

где   коэффициент теплоотдачи, Вт/(м²К); t_пов – температура поверхности тела; t_ж – температура окружающей среды.

Если коэффициент теплоотдачи достаточно большой (), то граничное условие (5) вырождается в граничное условие I-ого рода:

(2.6)

Теплообмен излучением поверхности тела с газом, вакуумом или окружающими телами описывается законом излучения:

(2.7)

где С  коэффициент излучения, Вт/(м²К⁴); Т_г – температура газа (окружающих тел), К; Т_пов – температура поверхности тела, К.

Уравнения (2.1)  (2.5) представляют систему дифференциальных уравнений, которые используются при математическом моделировании процесса нестационарной теплопроводности при соответствующем задании граничных условий. Эти же уравнения можно использовать для получения критериев подобия.

2.2 Описание процесса теплопроводности в безразмерном виде

Введем избыточную температуру, которая отсчитывается от постоянной температуры окружающей среды: . Тогда уравнения (2.1) (2.5) запишутся в следующем виде:

(2.8)

Пусть l – характерный размер тела, которым может быть его длина, толщина, полутолщина, радиус и т.п.; у образца и модели характерный размер определяется одинаково, но имеет различные значения. Рассмотрим безразмерные декартовые координаты:

(2.9)

Из (2.9) можно выразить размерные координаты:

(2.10)

В качестве масштаба для измерения температуры используем величину , используя которую введем безразмерную температуру:

откуда можно выразить размерную избыточную температуру

(2.11)

Подставляя выражения (2.10) и (2.11) в систему уравнений (2.8), получим:

Сократив на правую и левую части последних уравнений, их можно записать в следующем виде:

(2.12)

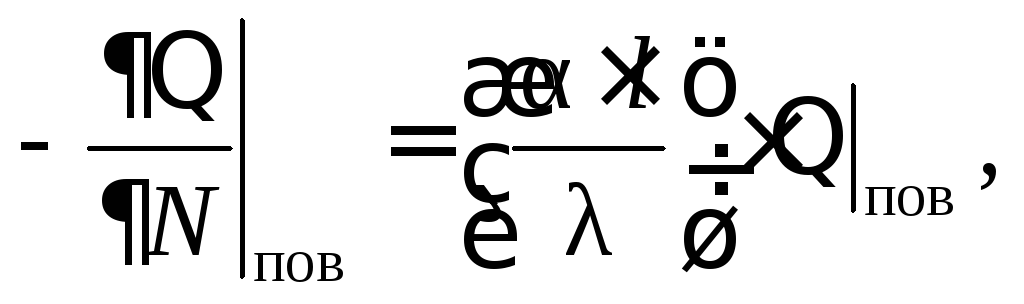
где N = n/l – безразмерная координата нормали.

В уравнениях (2.12) имеются безразмерные комплексы:

,

которые имеют свои названия и физический смысл. Критерий Fo является безразмерным временем и называется числом Фурье; критерий Bi является безразмерным коэффициентом теплоотдачи и называется числом Био.

С использованием чисел Fo и Bi система уравнений (2.12) записывается в следующем виде:

(2.13)

При условии большого коэффициента теплоотдачи (, ), числоBi  , и последнее граничное условие в системе (13) переходит в вид:

2.3 Уравнения подобия для процесса теплопроводности

Решение системы (2.13) можно представить в общем виде:

(2.14)

Выражение (2.14) называется уравнением подобия. В случае, когда Bi  (на практике данный случай возникает при Bi > 100), наступает автомодельность процесса относительно числа Bi, и уравнение (2.14) принимает вид:

(2.15)

Уравнения (2.14) и (2.15) соответствуют режиму охлаждения (нагрева) термически массивного тела.

В случае, если температурное поле зависит от двух координат (например, X и Y), уравнение подобия (2.14) принимает вид:

(2.16)

В случае одномерного температурного поля уравнение подобия имеет вид:

(2.17)

где Х – координата, вдоль которой изменяется температура.

Обычно на практике при исследовании охлаждения и нагрева тел интерес представляет изменение температуры в центре тела t_цен, и температуры на поверхности тела t_пов (или перепад температур в центре и на поверхности тела t = t_цен – t_пов). Тогда вместо уравнения (2.14) получаются уравнения:

(2.18)

где  безразмерные координаты центра тела;  безразмерные координаты поверхности тела.

В случае Bi   уравнения (2.18) преобразуются к виду:

(2.19)

Из аналитического решения системы уравнений (2.13) для тел простейшей геометрической формы (пластина, цилиндр, шар) известно, что начиная с некоторого времени  > ₀ (Fo > Fo₀) наступает регулярный режим охлаждения (нагрева) тела, когда уравнение (2.14) приближенно описывается формулой:

(2.20)

где А – коэффициент, зависящий от Bi; P – функция координат X, Y, Z; m – темп охлаждения (нагрева) тела, зависящий от геометрии и числа Bi:

Рассмотрим режим охлаждения (нагрева) когда коэффициент теплоотдачи  достаточно мал (  0), или линейный размер тела достаточно мал (l  0), так, что число Bi  0 (на практике этот случай возникает при Bi < 0,1). Данный случай соответствует охлаждению (нагреву) термически тонкого тела, когда во всех точках тела в данный момент времени температура практически одинакова. Иначе говоря, внутренний теплообмен внутри тела протекает гораздо быстрее, чем внешний теплообмен на поверхности, и температура по сечению тела успевает выравниваться.

В этом случае изменение избыточной температуры тела описывается дифференциальным уравнением:

(2.21)

где С – полная теплоемкость тела, Дж/К; F – площадь поверхности теплообмена с окружающей средой. Полную теплоемкость можно записать так:

(2.22)

где с – массовая теплоемкость, Дж/(кгК);  – плотность, кг/м³; – объем тела;– коэффициент, зависящий от геометрической формы тела.

Разделяя переменные в уравнении (2.21), с учетом (2.22) получим:

(2.23)

Интегрируя уравнение (2.23), получим:

или

(2.24)

Таким образом, при малых значениях числа Bi, уравнение подобия описывается выражением (2.24), где

В качестве примера в следующем пункте рассмотрим уравнения подобия при охлаждении (нагреве) плоской неограниченной пластины.

2.4 Охлаждение (нагревание) неограниченной пластины

Пластина толщиной  (толщина пластины много меньше ее других размеров) с начальной температурой t₀ в момент времени  = 0 начинает с одной стороны омываться жидкостью с температурой t_ж. Коэффициент теплоотдачи от пластины к жидкости равен . Другая сторона пластины остается адиабатной (плотность теплового потока через нее равна нулю: q = 0) и через нее теплота не передается. Коэффициент температуропроводности пластины а является постоянным.

На рис. 3 показана схема охлаждения пластины. Если ось х декартовой системы координат направить перпендикулярно пластине, то температура пластины будет зависеть от координаты х и от времени : t = t(x,).

Рис. 3. Схема охлаждения пластины.

Система уравнений (2.8) в данном случае принимает вид

(2.25)

где нормаль к поверхности пластины n совпадает по направлению с декартовой координатой x.

После приведения уравнений (2.25) к безразмерному виду получится система уравнений:

(2.26)

где Х = х/; Fo = a/²; Bi = /.

Аналитическое решение системы уравнений (2.26) известно и имеет вид:

(2.27)

где ₁, ₂, …, _n, …  бесконечный ряд возрастающих чисел  корней характеристического уравнения для пластины:

(2.28)

D_n – безразмерные коэффициенты:

Анализ показывает, что при Fo  0,3 ряд в (2.27) становится настолько быстросходящимся, что распределение температуры достаточно точно описывается первым членом ряда:

(2.29)

Выражение (2.29) соответствует случаю регулярного режима охлаждения, причем корень ₁ является функцией числа Bi.

Рассмотрим два частных случая: очень малого и очень большого числа Bi.

При Bi  0 (практически Bi < 0,1) корни характеристического уравнения (2.28) имеют значения:

₂ = ; ₃ = 2;…, _n =(n 1) .

Все коэффициенты ряда D_n  0, за исключением n = 1: D₁  1. Выражение (2.27) принимает вид:

(2.30)

В случае пластины ее характерным размером l является толщина : l = . Объем пластины равен V = F, где F – площадь охлаждаемой поверхности; тогда для пластины коэффициент и выражение (2.30) является частным случаем выражения (2.24).

При Bi   (практически Bi > 100) корни характеристического уравнения (2.28) имеют значения:

₁ = /2; ₂ = 3/2; ₃ = 5/2;…, _n =(2n 1) /2.

Коэффициенты D_n в этом случае имеют значения:

Решение (2.27) принимает следующий вид:

(2.31)

Из выражения (2.31) следует, что в случае Bi    зависит от X и Fo, и не зависит от Bi.

На охлаждаемой поверхности пластины при Х = 1 безразмерная температура  = 0, т.е. охлаждение пластины происходит при граничных условиях I-ого рода, когда температура на поверхности тела практически равняется температуре охлаждающей жидкости.

2.5 Нагревание тела в условиях теплообмена излучением

В высокотемпературных печах (температура в рабочем пространстве превышает 1000 С) нагревание твердого тела протекает в основном за счет теплообмена излучением на поверхности тела, и теплообмена за счет теплопроводности внутри тела. В вакууме охлаждение тела также протекает за счет излучения с поверхности. Примем, что в начальный момент времени  = 0 начальная температура тела во всех точках одинакова и равна t₀. Внутренние источники теплоты отсутствуют.

Температурное поле в твердом теле в декартовой системе координат описывается дифференциальным уравнением теплопроводности:

, (2.32)

где t = t(x,y,z,) – температурное поле; x, y, z – декартовы координаты;  – время; а – коэффициент температуропроводности.

Начальное условие для уравнения (2.32) записывается так:

(2.33)

На адиабатной поверхности тела условие теплообмена имеет вид:

(2.34)

где n – координата нормали к поверхности тела.

Теплообмен излучением поверхности тела с рабочим пространством печи (газом, вакуумом или окружающими телами) описывается законом излучения:

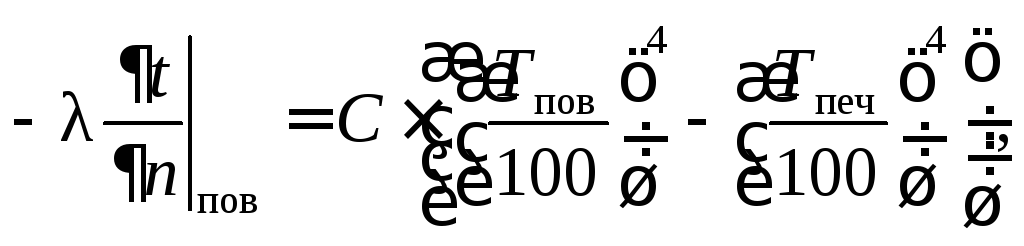(2.35)

где С  коэффициент излучения, Вт/(м²К⁴); Т_пов = t_пов + 273,15 – абсолютная температура поверхности тела, К; Т_печ = t_печ + 273,15 – абсолютная температура рабочего пространства печи (окружающей среды), К.

Вместо температуры t, C, удобно использовать абсолютную температуру T = t + 273,15 К. Тогда уравнения (2.32) – (2.34) можно записать в виде:

(2.36)

где Т = t(x,y,z,) + 273,15 – абсолютная температура тела;

(2.37)

где Т₀= t₀ + 273,15 – абсолютная начальная температура тела;

(2.38)

Приведем уравнения (2.36) – (2.38) к безразмерному виду. Пусть l – характерный размер тела. Безразмерные декартовые координаты:

Размерные координаты можно записать так:

(2.39)

В качестве масштаба для измерения температуры используем величину Т_печ, используя которую введем безразмерную температуру:

Размерную температуру можно выразить так:

(2.40)

Подставив выражения (2.39) и (2.40) в уравнения (2.36) – (2.38), получим:

(2.41)

(2.42)

где – число Фурье;– безразмерная начальная температура;N = n/l – безразмерная координата нормали.

Приведем уравнение (2.35), описывающее теплообмен излучением, к безразмерному виду, используя выражения (2.39) и (2.40):

или

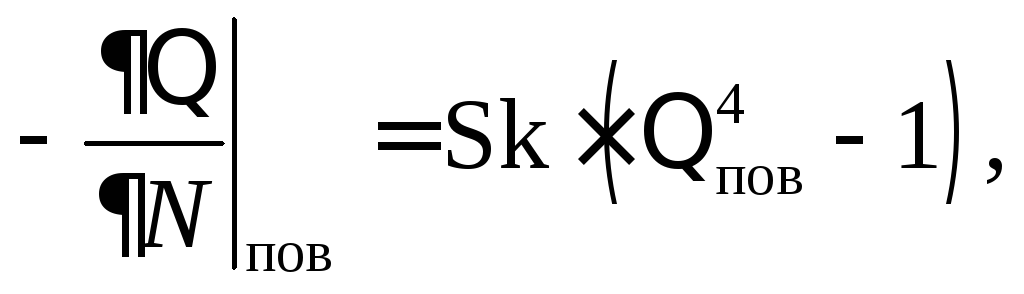(2.43)

где  безразмерная температура поверхности тела; Sk  безразмерный критерий Старка:

Таким образом, нагревание (охлаждение) твердого тела в условиях теплообмена излучением в безразмерном виде описывается системой уравнений (2.41) – (2.43). Уравнением подобия является решение данной системы в следующем виде: (2.44)

Отметим, что в отличии от задачи охлаждения при конвективном теплообмене, рассмотренной в п. 2.2, безразмерная температура ₀ в данном случае не равна единице, и входит дополнительным критерием подобия в уравнение (2.44).

Если рассматривать конкретные точки тела, например, центра и поверхности, то уравнения подобия принимают вид:

2.6 Процессы стационарной теплопроводности

В случае стационарной теплопроводности в твердом теле температурное поле не зависит от времени: t/ = 0. Стационарное температурное поле в твердом теле без внутренних источников теплоты с постоянным коэффициентом теплопроводности в декартовой системе координат описывается дифференциальным уравнением теплопроводности:

(2.45)

Начальное условие (2.3) в данном случае исключается.

Чтобы имелось нетривиальное решение уравнения (2.45), тело должно иметь как минимум две теплообменных поверхности, через одну из которых оно будет получать теплоту от горячего теплоносителя с температурой t_ж1, а через другую – отдавать теплоту холодному теплоносителю с температурой t_ж2. Также у тела могут быть адиабатные поверхности, на которых теплообмен отсутствует и описывается выражением (2.4).

Конвективный теплообмен на горячей и холодной поверхностях тела описывается выражениями:

(2.46)

где ₁ и ₂  коэффициенты теплоотдачи на горячей и холодной поверхностях, Вт/(м²К); t_пов1, t_пов2 – температуры горячей и холодной поверхностей тела; t_ж1, t_ж2 – температуры горячего и холодного теплоносителя.

Схема теплообмена при стационарной теплопроводности показана на рис. 4.

После приведения к безразмерному виду уравнения (2.45) и (2.46) примут вид:

(2.47)

где безразмерная температура определяется выражением:

критерии Био для горячей и холодной поверхности:

Bi₁ = ₁l/; Bi₂ = ₂l/.

Рис. 4. Схема теплообмена при стационарной теплопроводности.

Решением системы уравнений (2.47) является уравнение подобия:

(2.48)

При Bi₁   температура горячей поверхности становится равной температуре горячего теплоносителя: t_пов1 = t_ж1. В этом случае уравнение подобия (2.48) переходит в такое:

(2.49)

При Bi₂   температура холодной поверхности становится равной температуре холодного теплоносителя: t_пов2 = t_ж2, и (2.49) примет вид:

(2.50)

В качестве примера рассмотрим стационарную теплопроводность в плоской пластине толщиной , при условии Bi₁  , Bi₂  , таким образом, на поверхностях пластины заданы постоянные температуры t_пов1, t_пов2. Если ось х направить перпендикулярно пластине, температура будет зависеть только от х. Схема стационарной теплопроводности в пластине показана на рис. 5.

Рис. 5. Стационарная теплопроводность в пластине.

Система уравнений (2.47) в данном случае принимает вид:

; (2.51)

где безразмерная температура определяется выражением:

Решением системы (2.51) является выражение:

(2.52)

Как следует из выражения (2.52), при стационарной теплопроводности температура изменяется линейно по толщине пластины. Простота уравнения (2.52) связана с простой геометрической формой пластины, а также постоянством коэффициента теплопроводности , в результате чего уравнение теплопроводности имеет простой вид.

2.7 Моделирование процессов теплопроводности

При физическом моделировании теплопроводности необходимо обеспечить геометрическое подобие образца и модели. Модель выполняется как уменьшенная копия реального твердого тела с линейным масштабом с_l = l/l, где l и l  характерные линейные размеры образца и модели. Выбираются геометрически подобные системы координат для образца (х,y,z) и модели (х,y,z), как показано на рис. 6.

Рис. 6. Геометрическое подобие образца и модели.

На поверхности модели организуются условия теплообмена, подобные условиям на поверхности образца. Так, при конвективном теплообмене нужно обеспечить адиабатность соответствующих поверхностей и равенство чисел Био для образца и модели на поверхности (или поверхностях) теплообмена: Bi = Bi, или

l/ = l/, (2.53)

где ,   коэффициенты теплоотдачи, ,   коэффициенты теплопроводности на поверхности образца и модели.

Из условия (2.53) вытекает, что коэффициенты теплопроводности материалов образца и модели должны соотноситься так:

/= с_l /. (2.54)

Если охлаждение (нагревание) образца и модели происходит в одинаковой среде, то коэффициенты теплоотдачи  и  имеют одинаковый порядок величины. Допустим,  = . Тогда, если модель имеет линейный размер в 10 раз меньше (с_l = 10), то из (2.54) следует, что коэффициент теплопроводности модели  должен быть в 10 раз меньше, чем у образца.

Поскольку условие (2.53) сложно выдержать точно, то исследования на модели проводят при разных числах Bi. Для этого на поверхности модели за счет изменения скорости циркуляции среды или вида среды обеспечивают разные коэффициенты теплоотдачи ₁, ₂,…, _n, которым соответствует ряд чисел Био: Bi₁, Bi₂,…, Bi_n.

Достаточно просто организовать условия теплообмена I-ого рода, когда критерий Bi выбирается достаточно большим (Bi ), что на практике требует значения Вi > 100. Для этого нужно выбрать материал модели, имеющий достаточно низкий коэффициент теплопроводности .

При изучении процесса охлаждения (нагревания) модель предварительно разогревают до температуры t₀, превышающей на несколько десятков градусов температуру t_ж охлаждающей среды (жидкости, неизлучающего газа). Температура t_ж как правило равна температуре окружающей среды.

Равномерно разогретая модель в момент времени  = 0 помещается в охлаждающую среду. В процессе охлаждения в характерных точках модели (обычно в центре и на поверхности) с безразмерными координатами X_x, Y_x, Z_x измеряется изменяющаяся со временем температура t_х(), где   время, прошедшее с начала охлаждения модели. Для измерения нужно использовать достаточно быстродействующие датчики температуры (например, термопары), предварительно установленные в характерные точки модели. Вторичный прибор должен регистрировать значения температуры и времени.

Результаты измерений обрабатываются в виде уравнения подобия:

(2.55)

где безразмерные критерии определяются выражениями

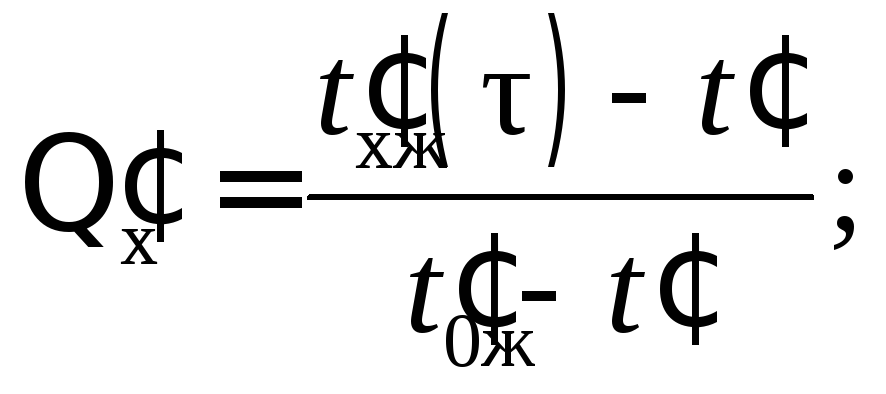
где а = /(с)  коэффициент температуропроводности; с,   массовая теплоемкость и плотность материала модели.

Зависимость (2.55) графически имеет вид, показанный на рис. 7, где по шкале ординат отложена безразмерная температура  в логарифмических координатах. При регулярном режиме охлаждения ln() линейно уменьшается в зависимости от Fo при данном значении числа Bi.

Рис. 7. Графическая зависимость

При выполнении условий подобия, уравнение подобия (2.55) будет применимо для расчета процесса охлаждения (нагревания) образца, т.е. при наличии геометрического подобия модели и образца, при равенстве чисел Био и Фурье, будут одинаковыми безразмерные температуры:

где Fo и _х  число Фурье и безразмерная температура образца:

;

где t₀ – начальная температура образца; t_ж – температура среды, где охлаждается (нагревается) образец; t_х() – температура в характерной точке образца в момент времени  после начала охлаждения.

Характерные точки образца должны иметь такие же безразмерные координаты, как и координаты модели:

X_x=X_x, Y_x = Y_x, Z_x= Z_x.

Размерная температура в характерной точке образца в нужный момент времени определяется выражением:

(2.56)

В случае нагревания (охлаждения) тела в условиях теплообмена излучением вместо чисел Био нужно обеспечить равенство чисел Старка для модели и образца: Sk = Sk, или:

(2.57)

где С, С – коэффициенты излучения для модели и образца; Т_печ, Т_печ – температуры окружающей среды в случае модели и образца.

Кроме того, в случае теплообмена излучением нужно обеспечить равенство безразмерных начальных температур: ₀ = ₀, или:

(2.58)

где Т₀, Т₀ – начальные температуры модели и образца, К.

Условие (2.58) накладывает серьезное ограничение на выбор температур Т₀ и Т_печ в образце; поэтому обычно принимают:

Т₀ = Т₀; Т_печ = Т_печ,

тогда автоматически выполняется условие (2.58).

Если принять, что Т_печ = Т_печ, и С С, то из условия (2.57) вытекает, что коэффициенты теплопроводности в модели и образце соотносятся так:

/  l/l = c_l. (2.59)

Т.е., если модель имеет линейный размер в 10 раз меньше (с_l = 10), то из (2.59) следует, что коэффициент теплопроводности модели  должен быть в 10 раз меньше, чем у образца.

Так как условие (2.57) сложно выдержать точно, то проводят исследование при различных числах Sk. Для этого можно, например, изменять в модели линейный размер тела l. Результаты исследования представляют в виде графических зависимостей:

(2.60)

где Т_х – абсолютная температура в характерной точке модели; а = /(с)  коэффициент температуропроводности; с,   массовая теплоемкость и плотность материала модели.

Полученные зависимости (2.60) можно применять для реального образца, если имеется подобие. Если выполняется равенство

Fo = Fo, Sk = Sk , ₀ = ₀,

то будет выполняться равенство

_х = _х.

Размерная температура образца находится по выражению:

В случае стационарной теплопроводности необходимо обеспечить подобие условий теплообмена поверхностях образца и модели, где подводится или отводится теплота:

Bi₁ = Bi₁; Bi₂ = Bi₂, или

₁l/= ₁l/; (2.61)

₂l/= ₂l/,

где ₁, ₁ – коэффициенты теплоотдачи на обогреваемой поверхности модели и образца; ₂, ₂ – коэффициенты теплоотдачи на охлаждаемой поверхности модели и образца.

При выполнении условий (2.61) безразмерные температуры образца и модели будут одинаковы:

где t(x,y,z), t(x,y,z) – температурные поля образца и модели; х = с_lx; y = с_ly; z = с_lz; t_ж1, t_ж1 – температуры горячей среды; t_ж2, t_ж2 – температуры холодной среды в случае образца и модели.

Размерная температура образца определятся по выражению: