1 Теория подобия

В данном разделе введены основные понятия теории подобия, рассмотрено применение теории подобия к потокам реальной жидкости, сформулированы основная теорема теории подобия и понятие автомодельности. Рассмотрены метод размеренностей и сформулировано основное правило моделирования.

1.1 Основные понятия теории подобия

В большинстве случаев процессы, протекающие в технических устройствах, настолько сложны, что получить для них аналитические, хотя бы и приближенные, решения невозможно. Очень часто и численное решение соответствующих задач либо сопряжено с большими трудностями, либо также при современных возможностях ЭВМ, практически не возможно.

В такой ситуации единственной возможностью решения задачи оказывается экспериментальное исследование. Однако экспериментальные данные, полученные в результате такого исследование справедливы, строго говоря, только для конкретных условий данного единственного эксперимента. Таким образом, возникают следующие два вопроса:

1) Каким образом должны быть обработаны экспериментальные данные, чтобы они имели некоторую общность, то есть были бы справедливы не для единственного явления или процесса, а для некоторой их совокупности?

2) На какую совокупность явлений можно распространять обработанные указанным способом результаты единичного экспериментального исследования?

С этими двумя вопросами тесно связана проблема моделирования физических и физико-химических процессов, протекающих в технических устройствах. Дело в том, что непосредственное экспериментальное исследование этих процессов на натурных объектах часто оказывается весьма затруднительным, или вообще невозможным. В результате возникает необходимость моделирования этих процессов в лабораторных условиях и на лабораторных установках. Понятно, что модель должна быть сооружена так и процессы в ней должны протекать таким образом, чтобы результаты их экспериментального исследования могли быть перенесены на образец.

Ответ на все эти вопросы и должна дать теория подобия, которая представляет собой научную основу обобщения экспериментальных данных и моделирования различных физических и физико-химических процессов.

Наибольший вклад в создание теории подобия применительно к тепловым процессам внесли ученые Кирпичев М.В., Михеев М.А., Эйгейсон Л.С., Гухман А.А.

Важнейшими понятиями теории подобия являются понятия класса и группы явлений. Классом физических явлений (процессов) называется такая их совокупность, которая характеризуется физическим механизмом, лежащим в основе этих явлений и потому описывается одной и той же системой дифференциальных уравнений. Класс представляет собой наиболее широкую совокупность явлений одной и той же физической природы. Примерами классов явлений могут служить течение идеальной и реальной жидкости. Понятно, что в класс входит бесчисленное множество единичных явлений. В соответствии с этим система дифференциальных уравнений, описывающая все явления данного класса, имеет бесчисленное множество частных решений, каждое из которых соответствует определенному единичному явлению из данного класса.

Для того чтобы выделить из класса определенное единичное явление и, соответственно, для того чтобы получить частное решение системы уравнений необходимо задать условия однозначности определяющие всю специфику данного единичного явления. В условия однозначности входят геометрические и физические свойства системы, а также краевые условия.

Под геометрическими свойствами системы понимают форму и размеры тел, составляющих систему. Например, если речь идет о течении жидкости, должны быть заданы форма и размеры сосуда, либо канала, где проходит движении или форма и размеры тела обтекаемого потоком жидкости.

В физические свойства системы входят значения физические параметра тел, составляющих систему, или их зависимость от характеристик процесса, либо от координат и времени, если эти параметры изменяются. Например, в случае движения жидкости должны быть заданы ее плотность и вязкость, а также ускорение силы тяжести, либо зависимость плотности и вязкости от температуры и давления, если эти параметры рассматриваются как переменные величины.

Краевые условия содержат начальные и граничные условия задачи. В качестве начальных условий, имеющих смысл лишь для нестационарных процессов, задаются распределения величин, подлежащих определению (теоретическому или экспериментальному), в начальный момент времени. В случае нестационарного движения жидкости в этот момент должны быть заданы распределения скорости и давления.

Граничные условия описывают взаимодействие системы с окружающей средой. Например, в качестве граничных условий могут быть заданы значения определяемых величин на границах системы. В случае движения реальной жидкости сначала задаются распределения скорости и давления на входе в канал и на выходе из него, а также условия прилипания на твердых поверхностях, то есть нулевое значение скорости на стенках канала.

Таким образом, класс  это наиболее широкая совокупность однотипных явлений, единичное явление  наиболее узкая. Промежуточное положение между этими совокупностями занимает группа явлений представляющая собой совокупность подобных физических явлений.

Теория подобия физических явлений возникла как последовательное обобщение представленией о геометрическом подобии. Поэтому поясним некоторые важные понятия теории подобия вначале на геометрическом примере.

Рассмотрим класс плоских фигур, называемых прямоугольниками, и представляющих собой четырехугольники с прямыми углами между сторонами. В этот класс входит бесчисленное множество единичных фигур, отличающихся одна от другой численным значением длин сторон.

Если две стороны а и b какого либо прямоугольника умножить на одну и туже величину k_l, получим прямоугольник со стороной и, подобный первому. Придавая множителю преобразованияk_l разные значения получим бесчисленное множество фигур, входящих в класс прямоугольников и составляющих группу фигур, то есть совокупность подобных прямоугольников.

Понятно, что множитель преобразования k_l связывает между собой не только сходственные стороны, но и все сходственные линейные элементы подобных геометрических фигур и тел. Например диагональ m второго из упомянутых выше подобных прямоугольников также связана с диагональю первого m соотношением . Ясно также, что множитель преобразования для нелинейных элементов подобных фигур или тел будет отличаться от множителя преобразования линейных элементов, но будет одним и тем же для всех сходных одноименных элементов. В данном примере множитель преобразованииk_s площадей подобных прямоугольников определяемый соотношением , разумеется, не равенk_l. Легко сообразить, что k_s = k_l². Однако он будет одним и тем же для всех сходственных элементов площади. Например, площади треугольников образованные отрезками диагоналей и сходственными сторонами, будут в подобных прямоугольниках связаны между собой тем же множителем преобразования k_s..

Таким образом, применительно к геометрическому подобию множитель преобразования может быть определен как безразмерная величина, представляющая собой отношение сходственных однокомпонентных элементов двух различных фигур или тел. Если эти две фигуры и тела подобны, то множители преобразования для всех одноименных, то есть имеющих одинаковую размерность, элементов одинаковы.

Точно также можно ввести понятие множителя преобразования и для физических явлений (процессов), определив его как отношение одноименных (например, скоростей или давлений) характеристик двух физических процессов в сходственные моменты времени в сходственных точках. Если эти два процесса подобны, то множители преобразования представляют собой постоянные величины, не зависящие от координат и времени.

Однако в подобии геометрических фигур можно убедиться и другим способом. Рассмотрим, например безразмерную величину k_l = a/b, представляющих собой отношение двух сторон какого-либо прямоугольника. Ясно, что эта величина, называемая критерием или числом подобия будет одной и той же для всех подобных между собой прямоугольников, то есть для всех этой группы фигур:

k_l = a/b =a/b=a″/b″=….

Это обстоятельство принято обозначать следующим образом: k_l = idem, где idem обозначает «тоже самое», т.е. для всех подобных фигур критерий подобия имеет одну ту же величину.

Таким образом, критерий подобия представляет собой безразмерную величину, представляющую собой комбинацию величин определяющих элементы данной фигуры или тела. Для всех подобных фигур или тел такая комбинация имеет одно и тоже значение.

Заметим, что критерий или число подобия не обязательно должен быть выражен как отношение элементов, имеющих одну и ту же размерность. Например, ясно, что для всех подобных прямоугольников отношение площади к квадрату одной из сторон так же является одной и той же величиной, т.е. также представляет собой критерий подобия. Действительно, величина

,

очевидно, будет одинакова для всех подобных прямоугольников.

Точно также для подобных физических явлений могут быть записаны безразмерные величины, критерии или числа подобия, образованные из величин, характерных для каждого данного явления и одинаковые для всех подобных явлений или процессов.

Таким образом, подобными физическими явлениями, образующими группу, называются явления одной физической природы принадлежащих к одному классу (и, следовательно описываемые одной и той же системой дифференциальных уравнений) и отличающихся одно от другого лишь масштабами. Все характеристики любого из таких явлений, либо могут быть получены из одноименных характеристик любого другого явления подобному данному, т. е. принадлежащего к той группе, путем умножения на соответствующие множители преобразования, являющимися постоянными величинами.

Понятно, что все многообразие каждого единичного явления, входящего в группу подобных явлений, сосредоточено в условиях однозначности, эти условия для явлений одной группы должны быть подобны, т.е. должны отличатся лишь множителем преобразования. Ясно, в частности, что подобными могут быть, лишь такие процессы, которые происходят в геометрически подобных системах, поскольку геометрические свойства системы входят в условия однозначности.

1.2 Применение теории подобия к потокам реальной жидкости

Введенные выше понятия теории подобия рассмотрим на примере движения жидкости и газа. На рис. 2 показаны два случая движения жидкости в круглой трубе.

Для потока жидкости представленного на рис. 2а, на некотором расстоянии x от входа в трубу распределение скорости изображается кривой u(y), где y  текущий радиус, изменяющийся от 0 до r₀ (r₀  радиус трубы). Если теперь рассмотреть распределение скорости в сходственном сечении второй трубы (рис. 2б), отстающем на расстоянии x = k_lx от входа в нее, и если при этом окажется, что в каждой точке этого сечения с текущим радиусом y= k_lу скорость u определяется соотношением u(y) = k_uu(y), где k_u – множитель преобразования скорости, то это означает что второй поток подобен первому потоку жидкости. Очевидно, что при этом линейный множитель преобразования k_l определяется как отношение диаметров (или радиусов) труб k_l = r₀/r₀, а множитель преобразования скорости k_u – как отношение характерных скоростей, например средних по сечению k_u = u₀/u₀.

а)

б)

Рис. 2. Подобные течения вязкой жидкости в круглой трубе.

В подобии рассмотренных потоков можно убедиться и другим способом, используя понятие критериев подобия. Эти потоки будут подобны, если при одинаковых значениях безразмерного расстояния от входа, т.е критерия X = x/r₀ = x/r₀ и при одинаковых значениях безразмерного расстояния от оси, т.е критерия Y = y/r₀ = y/r₀, безразмерные скорости будут одинаковы, т.е. U = u/u₀ = u/u₀. Таким образом, эти потоки будут подобны, если при выполнении условий X = idem и Y = idem, получим U = idem.

Понятно, что можно реализовать бесчисленное множество таких подобных течений, образующих группу подобных явлений.

Важным вопросом, имеющим практическое значение при моделировании различных процессов является вопрос о том, являются ли все множители преобразования независимыми или между ними имеются какие-то связи. С точки зрения моделирования этот вопрос сводится к проблеме выбора множителей преобразования. Решая эту проблему, необходимо знать, можно ли придавать множителем преобразования произвольные, например удобные для моделирования значения, если при этом имеются некоторые ограничения.

Для отыскания ответа на указанный вопрос рассмотрим два нестационарных потока реальной жидкости, движущейся в поле силы тяжести. Будем считать, что эти потоки подобны между собой и выясним, имеются ли при этом какие-то связи между множителями преобразования.

Пусть уравнение движения для первого из рассматриваемых потоков имеет вид:

(1.1)

где u = u(x,y,)  поле скорости жидкости; х, у  декартовы координаты;   время; g  ускорение свободного падения; р, ,   давление, плотность и коэффициент кинематической вязкости жидкости.

Поскольку второй поток подобен первому, он описывается таким же уравнением:

(1.2)

в котором штрихом отмечены параметры, независимые переменные и функции, относящиеся ко второму потоку. При этом из подобия рассматриваемых потоков следует, что все эти величины пропорциональны соответствующим величинам для первого потока, а коэффициентами пропорциональности являются множитель преобразования, т.е.

g = k_gg; ρ = k_ρρ; ν = k_νν; τ = k_ττ;

x = k_lx; y = k_ly; u = k_uu; p = k_pp.

Подставляя эти выражения в уравнения (1.2) и учитывая, что множители преобразования постоянны, а потому могут быть вынесены за знаки производных и дифференциалов, получим:

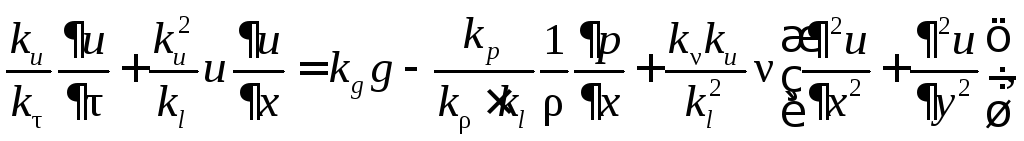(1.3)

или разделив обе части (1.3) на , получим:

(1.4)

Поскольку рассматриваемые потоки подобны, они должны описываться тождественными уравнениями. Следовательно, уравнение (1.4) должно быть тождественно уравнению (1.1). Это требование будет выполнено только в том случае, если постоянны коэффициенты перед всеми членами в уравнении (1.4), составление из множителей преобразования, будет равны единице, как это уже имеет место для второго слагаемого в левой части уравнения (1.4).

Таким образом, получим следующие соотношения между множителями преобразования:

(1.5)

Равенства (1.5) найдены, исходя из условия, что рассматриваемые потоки подобны, а потому представляют собой необходимые условия подобия двух потоков жидкости.

Таким образом, из семи множителей преобразования (k_g, k_ρ, k_ν, k_l, k_p, k_u и k_τ) лишь любые три можно выбрать произвольно. Четыре остальные должны определяться из условий (1.5).

Равенства (1.5) можно записать в ином виде. Для этого множители преобразования выразим как отношения соответствующих для первого и второго потоков, подставим эти выражения в равенства (1.5) и разнесем величины, характерные для каждого из потоков, по разные стороны от знака равенства. Например, в первое соотношение (1.5) подставим k_l = l/l , где l и l  характерные размеры первого и второго потоков, соответственно, k_u = u₀/u₀, где u₀ и u₀ – характерные (заданные) скорости для первого и второго потоков, соответственно, k_τ = τ/τ.

В результате вместо первого из равенств (1.5) получим:

.

Полученная безразмерная величина

называется критерием или числом гомохронности. Таким образом, одним из условий подобия является равенство чисел гомохронности для двух потоков, т.е. Но = idem.

Легко видеть, что в число гомохронности входят два постоянных параметра задачи – характерная скорость и характерный размер и независимая переменная – время. Таким образом, число гомохронности также является переменной величиной и представляет собой безразмерное время. Смысл этого утверждения заключаются в том что равенство чисел гомохронности, т.е. условия Но = idem, определяет сходственные моменты времени для двух сравниваемых потоков. Например, распределения скоростей в этих двух потоках будет подобным не в один и тот же момент времени τ = τ, а в сходственные моменты времени, определяемые условием Но = idem, т.е. условием .

Проделав такую же операцию со вторым из равенств (1.5) получим:

. (1.6)

Безразмерная величина

называется числом или критерием Фруда, представляет собой безразмерный параметр задачи, так как все ее величины, входящие в выражения для Fr, являются постоянными параметрами.

Из третьего равенства (1.5) получаем:

(1.7)

где безразмерная величина

называется критерием или числом Эйлера. Этот критерий представляет собой безразмерное давление, т.е. безразмерную исконную функцию в рассматриваемой задаче. В выражение для критерия Эйлера входят два постоянных параметра (ρ и u₀) и искомая функция  давление, являющееся переменной величиной. Таким образом, критерий Эйлера также является переменной величиной.

Наконец, используя последнее из равенств (1.5) получим

. (1.8)

Безразмерная величина

называется критерием Рейнольдса. В данной задаче критерий или число Рейнольдса есть безразмерный постоянный параметр, так как все входящие в него размерные величины u₀, l и ν являются постоянными параметрами.

Проведенный анализ условий подобия двух потоков реальной жидкости позволяет сделать два важных вывода:

1) для подобия таких потоков необходимо, чтобы они протекали в геометрически подобных системах, чтобы подобными были условия однозначности и чтобы выполнялись следующие четыре условия: Но = idem; Еu = idem; Fr = idem; Re = idem, из которых первое просто определяет сходственные моменты времени, а три других являются необходимыми условиями подобия;

2) все безразмерные числа или критерии подобия можно разделить на три вида: безразмерные аргументы (например критерий гомохронности Но = u₀l/τ), безразмерные искомые функции (например критерий Эйлера ) ибезразмерные параметры (например число Фруда и Рейнольдса ).

Для выяснения физического смысла полученных критериев подобия (Eu, Fr, Re) рассмотрим поток реальной жидкости, который описывается тем же уравнением, что и проанализированные течения, но в стационарном режиме, когда , т.е. уравнением:

. (1.9)

Это уравнение представляет собой частный случай уравнения Навье-Стокса, и, следовательно, каждое слагаемое в нем имеет смысл массовой плотности определенной силы, действующей в потоке жидкости. В частности левая часть этого уравнения есть массовая плотность силы инерции f_ин, первое слагаемое в правой части – массовая плотность гравитационной силы тяжести f_т, второе слагаемое – массовая плотность силы давления f_д, и третье – массовая плотность силы внутреннего трения f_тр.

Найдем теперь порядок, т.е. приближенное значения каждой из этих величин, считая что, порядок скорости равен ее характерному значению u₀, т.е. О(u) = u₀, порядок координат равен характерному размеру потока l, т.е. О(x) = l, О(y) = l, а порядки g, p и ρ просто равны этим величинам. Тогда порядок массовой плотности силы инерции выразится как

;

порядок массовой плотности силы тяжести

О(f_т) = g;

порядок массовой плотности силы давлении

;

наконец порядок массовой плотности силы внутреннего трения

.

Сопоставляя эти выражения для порядков четырех сил, действующих в потоке с выражениями для критериев подобия, легко найдем что

Таким образом, критерий Эйлера, представляющий собой отношение порядков сил давления и инерции, является приближенной характеристикой соотношения этих сил. Точно также критерий Фруда характеризует соотношение сил инерции и гравитационных, а критерий Рейнольдса  сил инерции и внутреннего трения.

0. 1.3 Основная теорема теории подобия.

Выше было показано, что в том случае, когда два потока реальной жидкости являются подобными, все одноименные критерии подобия для этих потоков имеют одинаковые значения, т.е. равны между собой. Теперь необходимо выяснить, необходимо ли выполнения всех этих условий или достаточно обеспечить равенство лишь некоторых критериев, для того чтобы другие также оказались равными, и чтобы таким образом рассматриваемые потоки были подобными. Этот вопрос имеет непосредственное практическое значение с точки моделирования течения реальной жидкости.

Для решения указанной задачи рассмотрим двухмерное стационарное течение реальной несжимаемой жидкости, протекающей в поле действия силы тяжести, вектор массовой скорости (ускорения) которой направлен в вдоль оси 0х. Это течение описывается системой из трех уравнений с тремя неизвестными включающей два уравнения движения (Навье-Стокса) для осей х и у и уравнение неразрывности:

(1.10)

где u и w  компоненты скорости на оси х и у.

В результате решения сформулированной таким образом задачи (дополненную соответствующими граничными условиями) три искомые величины (два компонента вектора скорости u и w и давления р) определяются в виде функций от двух аргументов х и y и всех параметров задачи, в число которых входят плотность  и вязкость жидкости , ускорение силы тяжести g, характерное значение скорости u₀, заданное в граничных условиях задачи, и характерный размер потока l. Это решение, следовательно, должно иметь вид:

(1.11)

Такими образом каждая искомая величина является функцией двух аргументов и пяти параметров.

Выполним операцию приведения задачи к безразмерному виду. Это означает, что переменные величины, как функции, так и аргументы, фигурирующие в уравнениях (1.10) должны быть представлены безразмерными величинами, которые получаются путем деления размерной величины на соответствующий масштаб. В качестве масштаба приведения для скорости используют ее характерное значение u₀, для давления – величину , имеющую размерность давления, и для координат – характерный размер потокаl. Таким образом, получим безразмерные компоненты скорости

; ;

давления

,

и координат

;.

Для того чтобы ввести эти безразмерные величины в уравнение (1.10), подставим в них вместо размерных величин произведение безразмерных на соответствующие масштабы приведения. При этом масштабы как величины постоянные вынесем за знак производных и дифференциалов. В результате получим:

(1.12)

Для того чтобы все величины, фигурирующие в этих уравнениях, были безразмерными, необходимо обе части первых двух уравнений разделить на величину , а третье на величину. Тогда получим:

(1.13)

В этой системе в отличие от исходной (1.10) функционируют всего два безразмерных параметра Re и Fr и, следовательно, решение ее должно иметь вид зависимости трех безразмерных искомых функций U, W и Eu от двух безразмерных координат X, Y и от этих двух параметров, т.е.

U = U(X,Y,Re,Fr);

W =W(X,Y,Re,Fr); (1.14)

Eu = Eu(X,Y,Re,Fr).

Из полученного результата вытекают весьма важный вывод, заключающийся в следующем: для двух потоков, описываемых одинаковой системой уравнений, распространяющихся в геометрически подобных системах и характеризующихся подобием условий однозначности, зависимость безразмерных искомых величин скоростей и давления U, W и Eu и от безразмерных координат X, Y оказывается одинаковой, т.е. условия U = idem, W = idem, Eu = idem в сходственных точка (X = idem, Y = idem) выполняются при одинаковых значениях критериев Рейнольдса и Фруда, т.е. при выполнении условий Re = idem, Fr = idem. Следовательно, для таких потоков одинаковые значения критериев Рейнольдса и Фруда (Re = idem, Fr = idem) являются необходимыми и достаточными условиями подобия потоков. При этом условия U = idem, W = idem, Eu = idem в сходственных точках выполняются автоматически.

Критерии подобия, имеющие смысл безразмерных постоянных параметров задачи (в данном случае Re и Fr) и, следовательно, составленные из параметров, т.е. из условий однозначности, называются определяющими критериями. Критерии, имеющие смысл безразмерных искомых величин (в данном случае безразмерные скорости U, W и безразмерное давление, т.е. критерий Эйлера Eu) называются определяемыми критериями.

Определяющие критерии, как правило, характеризуют соотношение важнейших факторов, влияющих на развитие процесса, например, как показывает проведенный анализ, критерий Рейнольдса характеризует соотношение сил инерции и внутреннего трения, а критерий Фруда – силы инерции и гравитации.

Такой же анализ может быть проведен для любых процессов, имеющих математическое описание, что позволяет сформулировать необходимые и достаточные условия подобия таких процессов.

Процессы являются подобными, если они принадлежат к одному классу, т.е. описываются тождественными уравнениями, протекают в геометрически подобных системах, характеризуются подобием условий однозначности и равенством одноименных критериев, составленных из условий однозначности (определяющих). Приведенная формулировка составляет содержание так называемой основной теоремы теории подобия.

Таким образом, получен ответ на все вопросы, поставленные в начале настоящего раздела. Оказывается, что результаты единственного эксперимента можно распространять на группу явлений, т.е. на совокупность подобных явлений. При этом указанные результаты должны быть обработаны виде зависимостей безразмерных искомых величин (определяемых критерий) от безразмерных аргументов и от безразмерных параметров (определяющих критериев).

Сопоставление вида решений рассмотренной задачи, сформулированной в размерных величинах (1.11) и безразмерных (1.14), позволяет сделать еще один важный вывод, Оказывается, что в результате приведения задачи к безразмерному виду число величин, от которых зависят искомые функции, существенно сокращается. Действительно, если в решении (1.11), каждая из искомых функций зависит от двух аргументов и пяти параметров, то в решении (1.14) каждая из безразмерных искомых функций зависит от двух безразмерных аргументов и всего от двух безразмерных параметров. Это обстоятельство имеет большое практическое значение, так как облегчает графическое или табличное представление результатов теоретического или экспериментального решения задачи.

Возможность, сокращения числа аргументов или параметров задачи в результате перехода к безразмерным величинам утверждается так называемой π-теоремой теории подобия, в соответствии с которой любое уравнение (или система уравнений), связывающее между собой N физических величин, из которых К величин обладают независимыми размерностями, можно преобразовать к уравнению (или системе уравнений), связывающему N  К безразмерных критериев.

В рассматриваемой задаче в соответствии с этой теоремой число параметров уменьшилось на три.

1.4 Автомодельность

Как было сказано выше, каждый из определяющих критериев характеризует соотношение определенных физических факторов, оказывающих решающее влияние на рассматриваемый процесс. Очевидно, что в случае, когда один из этих факторов оказывается очень большим или напротив, очень малым, их соотношение перестает оказывать влияние на протекание процесса. При этом соответствующий критерий также оказывается либо очень большим, либо очень малым, а его изменение не сказывается более на ходе процесса. Это явление называют вырождением критерия или автомодельностью процесса (явления) по отношению к данному критерию. Смысл последнего термина заключается в том, что при изменении вырожденного критерия безразмерные характеристики процесса не изменяются, т.е. он остается подобным самому себе, моделирует сам себя.

Можно привести многочисленные примеры автомодельности различных явлений по отношению к некоторым определяющим критерием. Явление автомодельности существенно облегчает моделирование тех процессов, в которых оно реализуется.

5. Метод размеренностей

Метод основан на том факте, что решение физических задач не должно зависеть от выбора системы единиц, которая отражается только на численных коэффициентах уравнений, но не на их структуре. Безразмерные характеристики физического процесса подчиняются теореме Бэкингема (π-теореме) i = n  m, где i  наибольшее число безразмерных комплексов; n  число размерных параметров, характеризующих процесс; m  число первичных размерностей.

Анализ размерности рассмотрим на примере задачи о теплообмене в трубе при турбулентном течении.

Коэффициент теплоотдачи

зависит от скорости теплоносителя

,

коэффициента динамической вязкости

,

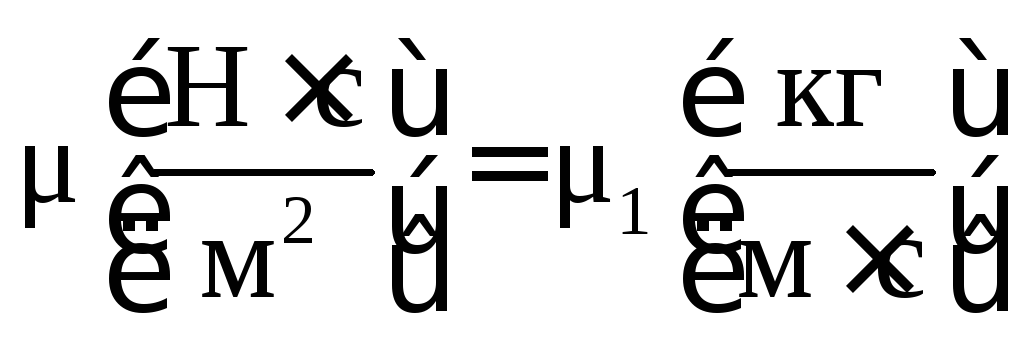удельной теплоемкости

,

коэффициента теплопроводности

,

ускорения силы тяжести

,

диаметра трубы d[м] и плотности

.

Длину трубы исключим из рассмотрения, так как рассматривается стабилизированный процесс теплообмена. Итого имеет 8 различных параметров, описывающих процесс. Число первичных размерностей равно пяти (джоуль (Дж), килограмм (кг), метр (м), кельвин (К), секунда (с)). Число безразмерных комплексов, характеризующих процесс, i = 8  5 = 3. Для определения этих комплексов применим алгебраический метод Рэлея. Для упрощения уравнений целесообразно сгруппировать некоторые величины, например, использовать не линейную скорость, а весовую w₁ = wρ. Тогда:

Суммирование показателей степени при одинаковых единицах приводит к следующей системе уравнений:

Дж… ;

кг… ;

м… ;

с…;

К… ;

Совместное решение этих уравнений дает:

; ;

;.

После подстановки в основное уравнение получим:

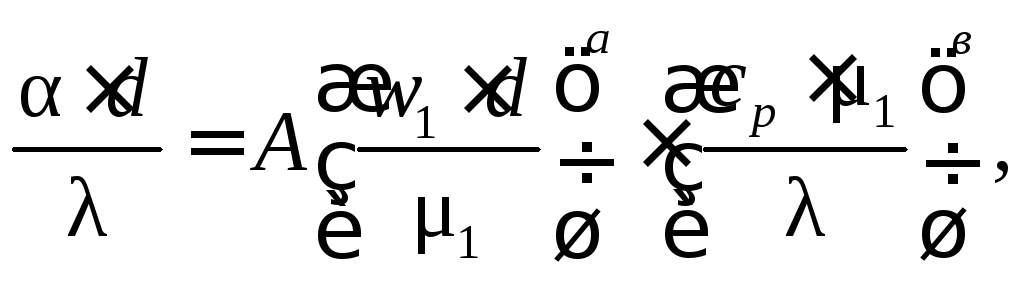
или

где Re – число Рейнольдса; Pr – число Прандтля;  число Нуссельта. Постоянные А, а, в должны определятся на основе модельных экспериментов.

Анализ размерностей является первичным звеном изучения процессов, когда еще не составлены уравнения, описывающие процесс. Успех дела здесь зависит от правильности определения физических величин, влияющих на процесс, что часто определяется интуицией исследователя. Наоборот, включение в рассмотрение величин, несущественных для данного процесса, приводит к неправильным критериям.

В приведенном выше примере числа Re и Pr являются определяющими критериями, а число Nu  определяемым. Если при использовании метода размерности решение задачи зависит от квалификации исследователя, то система критериев из анализа дифференциальных уравнений получается автоматически путем представления уравнений в безразмерной форме.

1.6 Основное правило моделирования

Как известно, метод моделирования позволяет распространить результаты исследования моделей технических устройств на натурные условия и получить обобщенные результаты, или, иными словами, осуществить на модели явление подобное натурному.

При моделировании процессов аэродинамики и теплообмена в технических устройствах, одноименные характеристики образца и модели должны отличатся друг от друга постоянными множителями – быть подобными. Простейшим аналогом такого условия является геометрическое подобие, например, подобие треугольников, при котором стороны треугольников отличаются одна от другой по длине соответственно в n раз.

Основное правило моделирования сформулировано впервые Кирпичевым М. В. и Гухманом А.А., гласит: подобны те системы, условия однозначности которых подобны, а критерии, составленные из условий однозначности, численно равны.

Полное подобие модели образцу определяется следующими условиями:

1. процессы в модели и в образце относятся к одному классу явлений;

2. эти процессы описываются одними и теме же уравнениями;

3. соблюдается геометрическое подобие;

4. безразмерные краевые условия численно равны;

5. определяющие критерии подобия численно равны.

Указанные пять условий определяют полное моделирование процесса. Точное воспроизведение в модели численных значений всех определяющих критериев при большом их числе и при условии геометрического подобия практически невозможно.

Как правило, прямое моделирование различными жидкостями можно проводить в случае одного определяющего критерия. Так, например, для задачи определения коэффициента гидравлического сопротивления в пучках труб в воздушном потоке таким критерием является число Re. В этом случае моделирование можно проводить как на воздухе, так и на жидкости. Если же необходимо определить и теплообменные характеристики, то вторым определяющим критерием будет число Прандтля Pr, значение которого для воздуха и жидкости существенно различны, и применение этой жидкости в качестве моделирующей для газовой задачи неприменимо. Так обстоит дело в случае двух определяющих критериев. При увеличении их числа задача еще более усложняется.

На практике, как правило, эти условия полного подобия не выполняются, что вынуждает переходить на приближенное моделирование, при котором в модели воспроизводится тот же физический процесс, что и в образце, при частичном нарушении некоторых из перечисленных пяти условий полного моделирования.

Одной из возможностей приближенного моделирования является проявление автомодельности процесса относительно какого-либо критерия. Говорят, что определяемая величина автомодельна относительно критерия подобия, если она не зависит от него. Если процесс автомоделен относительно какого-либо критерия подобия, то при моделировании отпадает необходимость соблюдать равенство этого критерия для образца и модели. Явление автомодельности дает возможность упрощения дифференциальных уравнений и условий однозначности. Члены уравнений (или условий однозначности), учитывающие факторы, относительно которых процесс оказывается автомодельным, могут быть опущены или видоизменены.

Возможна так же ситуация, когда воспроизводится только часть физического процесса. Применительно к теплообменникам используется метод локального теплового моделирования и локального аэродинамического моделирования. Особенность данного метода заключается в том, что подобие процессов стараются осуществить лишь в том месте, где производится исследование теплоотдачи. Например, если изучается теплоотдача при омывании жидкостью пучка труб, то в опытах в теплообмене может участвовать только одна из труб. Остальные трубы служат только для придания модели формы, подобной образцу. Данные по теплоотдаче получают из измерений, проведенных на единичной трубе. Предполагается, что теплоотдача испытуемой трубы в основном зависит от характера ее омывания, определяемого расположением системы труб, а не тепловыми условиями. Метод локального моделирования сравнительно прост и в ряде случаев позволяет получать достаточно точные результаты. Следует однако учитывать, что необоснованное применение метода локального теплового моделирования может привести и к значительным ошибкам.

Возможно так же моделирование по аналогии, когда в модели воспроизводится процесс другой физической природы, чем в образце, но описываемый одинаковыми безразмерными уравнениями. Примером моделирования по аналогии является моделирование процесса теплопроводности и потенциального в обтекания идеальной жидкостью процессом электропроводности.

Критерии подобия на практике определяются, или в результате анализа размерностей параметров, или в результате анализа дифференциальных уравнений, описывающих процесс.