
- •Министерство образования и науки российской федерации
- •Дифференциальные уравнения первого порядка
- •Уравнения с разделёнными и разделяющимися переменными
- •Однородные уравнения первого порядка
- •Линейные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Интегрирующий множитель
- •Дифференциальные уравнения высших порядков
- •Уравнения вида
- •Уравнения второго порядка, приводящиеся к уравнениям первого порядка
- •Линейные однородные уравнения. Определения и общие свойства
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения го порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения высших порядков
- •Системы обыкновенных дифференциальных уравнений
- •Системы линейных дифференциальных уравнений с постоянными коэффициентами
- •Р я д ы Числовые ряды Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакопеременные ряды
- •Функциональные ряды
- •Ряды Тейлора и Маклорена
- •Ряды Фурье
- •Ряды Фурье для четных и нечетных функций
- •Ряд Фурье для функции с периодом
- •К о м б и н а т о р и к а
- •Общие правила комбинаторики
- •Соединения в комбинаторике
- •Размещения без повторений
- •Перестановки без повторений
- •Сочетания без повторений
- •Размещения с повторениями
- •11 12 13 14 15 16 17 19
- •Перестановки с повторениями
- •Т е о р и я в е р о я т н о с т е й Случайные события Основные понятия теории вероятностей
- •Основные теоремы теории вероятностей Теорема сложения вероятностей несовместных событий
- •Зависимые и независимые события. Условная вероятность
- •Теорема умножения вероятностей
- •Теорема сложения вероятностей совместных событий
- •Вероятность появления хотя бы одного события
- •. Формула полной вероятности
- •Формула Бейеса
- •Повторение испытаний
- •Формула Бернулли
- •Локальная теорема Лапласа
- •. Формула Пуассона
- •Интегральная теорема Лапласа
- •Случайные величины Случайная величина. Виды случайных величин
- •Закон распределения вероятностей дискретной случайной величины
- •Числовые характеристики дискретных случайных величин
- •Математическое ожидание дискретной случайной величины
- •Дисперсия дискретной случайной величины
- •Плотность распределения вероятностей непрерывной случайной величины
- •Числовые характеристики непрерывных случайных величин
- •Законы распределений
- •Равномерное распределение
- •Нормальное распределение
- •. Правило трёх сигм
- •Показательное распределение
- •Функция надёжности
- •Элементы математической статистики Основные сведения из математической статистики
- •Статистическое распределение выборки. Полигон и гистограмма
- •1 4 6
- •10 15 25
- •Статистические оценки параметров распределения
- •Оценка генеральной дисперсии по исправленной выборочной
- •Точность оценки, доверительная вероятность (надёжность). Доверительный интервал
- •Методы расчёта сводных характеристик выборки
- •Сведение первоначальных вариант к равноотстоящим
- •Оценка отклонения теоретического и эмпирического распределений от нормального. Асимметрия и эксцесс
- •Элементы теории корреляции
- •. (1)
- •(4) . (5) Корреляционная таблица
- •Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
- •Методика вычисления выборочного коэффициента корреляции
- •. Статистическая проверка статистических гипотез
- •Линейное программирование Задача линейного программирования
- •Построение математической модели
- •Графическое решение задачи линейного программирования
- •Симплексный метод решения задачи линейного программирования
- •Решение задачи 1 симплексным методом
- •Искусственное начальное решение. Метод больших штрафов.
- •Особые случаи применения симплекс-метода
- •1.7.2 Бесконечное множество решений
- •1.7.4 Неограниченные решения
- •1.7.5 Промежуточное вырожденное решение
- •Задача о назначениях
- •4 Изменение запаса ресурса продукта а 7
- •1 Изменение единицы стоимости продукта а 4
- •Заключение
Симплексный метод решения задачи линейного программирования
Пусть имеется ЗЛП, записанная в стандартной форме:
max
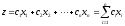 ,
(1)
,
(1)
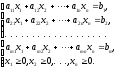 (2)
(2)
Обозначим
через
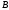 и
и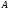 векторы-столбцы:
векторы-столбцы:

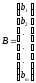 ,
,
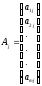
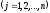 и через
и через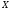 - вектор-строку
- вектор-строку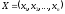 .
.
Тогда условия (1) и (2) можно записать в виде
max
 ,
,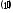 или
max
или
max
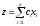 ,
,

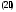
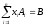
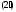
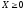
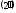
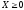
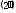
Прежде чем приступить
к обоснованию симплексного метода,
множество всех векторов
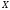 ,
удовлетворяющих условию
,
удовлетворяющих условию
 ,
обозначим через
,
обозначим через
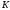 и
введем несколько определений:
и
введем несколько определений:
Определение 1. Линейная функция, определенная на выпуклом многограннике К, достигает своего оптимального значения в крайней точке этого многогранника.
Определение 2. Допустимая точка называется базисной или опорной (опорным планом), если она соответствует крайней точке многогранника решений;
Определение 3.
Допустимая точка называется вырожденной,
если менее чем
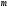 значений
значений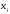 отличны от нуля (
отличны от нуля (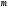 - число ограничений в задаче);
- число ограничений в задаче);
Определение 4.
Если X
– крайняя точка многогранника К, то не
более
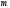 её координат
её координат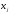 отличны от нуля, и векторы
отличны от нуля, и векторы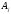 ,
коэффициенты
,
коэффициенты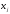 при которых отличны от нуля, линейно
независимы.
при которых отличны от нуля, линейно
независимы.
Пусть
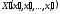 - крайняя точка многогранника решений
- крайняя точка многогранника решений ,
определяемого равенством
,
определяемого равенством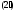 ,
причем
,
причем
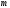 координат
координат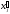 точки
точки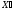 отличны от нуля, т.е.
отличны от нуля, т.е.
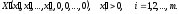
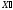 - невырожденный
опорный план задачи.
- невырожденный
опорный план задачи.
Согласно определению
4, векторы
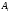
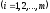 линейно независимы и образуют базис
линейно независимы и образуют базис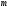 -мерного
пространства. Функция цели
-мерного
пространства. Функция цели в точке
в точке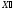 принимает значение
принимает значение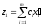
и
равенство
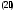 объединяется
в равенство
объединяется
в равенство
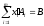 (3)
(3)
Найдём опорный план
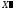 ,
которому соответствует значение
,
которому соответствует значение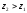 функции цели
функции цели .
Поскольку векторы
.
Поскольку векторы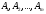 образуют базис, то любой вектор
образуют базис, то любой вектор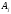 может быть представлен в виде линейной
комбинации этих векторов
может быть представлен в виде линейной
комбинации этих векторов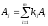 .
Выберем вектор
.
Выберем вектор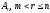 и, умножив его на число
и, умножив его на число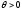 ,
прибавим к левой части равенства (3), а
затем вычтем из неё
,
прибавим к левой части равенства (3), а
затем вычтем из неё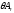 ,
в результате получим
,
в результате получим
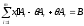 (4)
(4)
Так
как
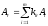 ,
то получим
,
то получим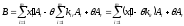 .
.
Таким образом, если
выбрать точку
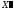 с координатами
с координатами
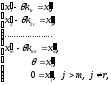
то
она будет удовлетворять условию
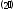 и, если при этом все координаты точки
и, если при этом все координаты точки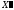 будут неотрицательны, т.е.
будут неотрицательны, т.е.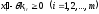 (5) , то
(5) , то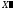 будет допустимой точкой задачи. Условие
(5) выполняется, если выбрать
будет допустимой точкой задачи. Условие
(5) выполняется, если выбрать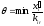 , (6)
, (6)
где
берётся min
только положительных отношений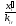 и
и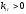 .
В случае, когда все
.
В случае, когда все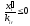
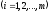 ,
величину
,
величину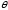 можно выбрать как угодно большой. Это
свидетельствует о неограниченности
многогранника решений. Пусть выбрано
можно выбрать как угодно большой. Это
свидетельствует о неограниченности
многогранника решений. Пусть выбрано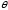 ,
удовлетворяющее условию (6); тогда имеем
в предположении, что
,
удовлетворяющее условию (6); тогда имеем
в предположении, что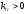 :
: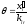 .
Координаты второй точки будут:
.
Координаты второй точки будут:
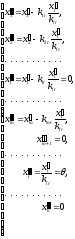
При
выборе
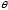 в соответствии с (6) обращается в нуль
лишь одна координата
в соответствии с (6) обращается в нуль
лишь одна координата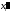 ,
поэтому новое решение
,
поэтому новое решение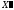 ,
как и старое
,
как и старое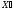 ,
содержит
,
содержит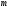 положительных координат. Таким образом
точка
положительных координат. Таким образом
точка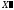 является опорным планом задачи и переход
от плана
является опорным планом задачи и переход
от плана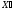 к плану
к плану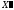 соответствует переходу от одной крайней
точки многогранника решений к другой.
соответствует переходу от одной крайней
точки многогранника решений к другой.
Выясним,
как следует выбирать вектор
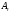 ,
чтобы при переходе от одной крайней
точки к другой линейная функция
,
чтобы при переходе от одной крайней
точки к другой линейная функция по крайней мере не убывала.
по крайней мере не убывала.
Точке
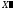 соответствует значение функции цели
соответствует значение функции цели ,
равное
,
равное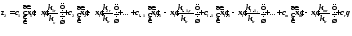
Преобразовав
это выражение для
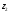 ,
получим
,
получим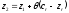 ,
где
,
где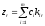 .
Очевидно
.
Очевидно ,
если
,
если .
.
Решение задачи 1 симплексным методом
max
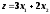 Стандартная формаmax
Стандартная формаmax
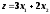
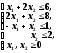
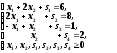
|
Ба- зис |
сz |
bi |
|
|
|
|
|
|
θ |
Замечания |
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
Результи- рующая строка |
zопт |
|
|
|
|
|
|
| ||
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
Результи- рующая строка |
zопт |
|
|
|
|
|
|
| ||
|
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
Результи- рующая строка |
zопт |
|
|
|
|
|
|
| ||
|
| ||||||||||
Презентация решения задачи 1 симплексным методом
