Линейное программирование Задача линейного программирования

Многие важные задачи экономики и планирования народного хозяйства, управления промышленностью тесно связаны с отысканием оптимального плана использования ограниченных ресурсов. Необходимость решения таких задач привела к широкому применению математических методов в экономике и планировании народного хозяйства и появлению нового раздела математики – математического программирования. В настоящее время завершена наиболее основательно часть этого нового раздела – линейного программирования.

Задача линейного программирования (ЗЛП) состоит в отыскании оптимального значения заданной линейной функции

( 1)

при условии, что на переменные 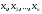наложены ограничения в виде линейных равенств или неравенств:

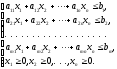( 2 )

Линейная функция Z, оптимальное значение которой отыскивается в ЗЛП, называется целевой функцией, или функцией цели.

Совокупность значений переменных 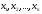, удовлетворяющих условиям ЗЛП и образующих область определения функцииZ, называется областью допустимых значений переменных, или просто допустимой точкой.

Набор значений 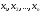из допустимой области, при котором целевая функцияZ принимает оптимальное значение, называется решением ЗЛП, или оптимальным планом.

Из теории экстремума функции многих переменных известно, что оптимальное значение функция нескольких переменных достигает или на границе области её определения, или внутри области определения, а именно, в одной из точек экстремума. Известно также, что необходимым условием экстремума функции многих переменных является обращение в нуль всех её частных производных во внутренней точке области определения. Но частные производные 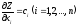линейной функции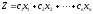нигде в области её определения одновременно в нуль не обращаются, следовательно, оптимальное значение функцияZ может принимать только на границе области.

Таким образом, рассматриваемая задача не может быть решена с помощью теории экстремума функции многих переменных, для решения её требуется применение особых математических приёмов, называемых методами линейного программирования.

Стандартная (каноническая) форма задачи линейного программирования

В практических задачах формы линейных условий, определяющих многогранник решений ЗЛП, могут быть очень разнообразны. Часть условий может быть задана в виде равенств, причем на некоторые переменные могут не налагаться требования неотрицательности. Это затрудняет исследование ЗЛП и главное – требует разработки специальных методов для решения каждого варианта задачи. Поэтому возникает необходимость ввести понятие стандартной формы ЗЛП.

При стандартной форме линейной модели

а) все ограничения записываются в виде равенств с неотрицательной правой частью;

б) значения всех переменных модели неотрицательны;

в) целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1. Исходное ограничение, записанное в виде неравенства типа 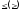, можно представить в виде равенства, прибавляяостаточную переменную к левой части ограничения (вычитая избыточную переменную из левой части).

Например, в левую часть исходного ограничения 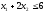вводится остаточная переменная, в результате чего исходное неравенство обращается в равенство.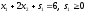

2. Рассмотрим исходное ограничение другого типа: 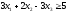. Для обращения исходного неравенства в равенство, вычтем из его левой части избыточную переменную. В результате получим.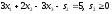

3. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части на -1. Например, неравенство 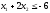заменить.

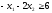Переменные

Любую переменную 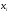, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных:.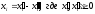

Целевая функция

Целевая функция линейной оптимизационной модели, представленной в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например, максимизация функции 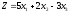эквивалентна минимизации функции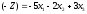. 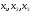Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменныхв обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.