3.2.4. Вывод в условиях неопределенности

Ситуации, когда определенный вывод по имеющимся фактам невозможен, часто встречаются в реальной жизни. Один из примеров - медицина. По одной и той же совокупности симптомов может быть сделан вывод о наличии у больного различных болезней. Вывод в этом случае будет зависеть в первую очередь от размеров и характера опыта врача (имеющихся у него эвристик и степени его в них уверенности) и от яркости проявления тех или иных симптомов (уверенности в правильности идентификации симптомов). Причем, откладывать решение о направлении лечения "до выяснения" иногда бывает неприемлемо.

Основные вопросы теории рассуждений в условиях неопределенности:

• количественное выражение степени уверенности в истинности или ложности факта;

• количественное выражение степени поддержки заключения конкретной посылкой;

• совместное использование нескольких посылок, независимо влияющих на заключение.

3.2.4.1. Математические основы вероятностных рассуждений

Математической основой вероятностных рассуждений являются формулы Байеса (условной вероятности). Вероятность события Aпри условии событияBравна:

p(A|B) = p(AB)/p(B)

Поскольку p(B|A) =p(AB)/p(A), то, выразив из этих формулp(AB) и приравняв два полученных выражения, имеем

p(A)*p(B|A) = p(B)*p(A|B).

Следующее важное правило - правило И/ИЛИ. Оно связывает вероятность появления хотя бы одного из заданных событий с вероятностью появления каждого из них и вероятностями их совместного появления.

Рассмотрим пример, наглядно иллюстрирующий все правила условной вероятности. Пусть из урны извлекаются шарики с пометками AиB, которые расставлены независимо друг от друга и могут присутствовать на шарике одновременно.

В этом случае

n- общее число шариков;

n₁- число шариков только с меткойA;

n₂- число шариков только с меткойB;

n₃- число шариков с меткамиAиB.

Вероятность извлечения помеченного шарика равна:

p(AB) = (n₁+n₂+n₃)/n

Произведем следующие допустимые преобразования:

p(AB) = (n₁+n₂+n₃)/n + n₃/n - n₃/n = (n₁+n₃)/n + (n₂+n₃)/n - n₃/n = p(A)+p(B)-p(AB)

Как нетрудно показать при помощи аналогичных преобразований, для случая трех разновидностей меток - A,BиCполучается:

p(ABC) = p(A)+p(B)+p(C) -p(AB) -p(AC)-p(BC)+p(ABC).

Общая формула для произвольного количества типов меток:

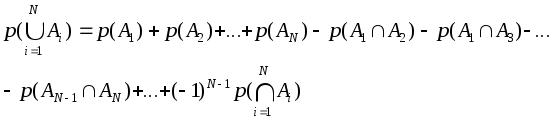
Следующее правило называется правилом композиции. Для описанного случая с метками двух типов справедливо:

p(A) = (n₁+n₃)/n = n₃/n + n₁/n = p(AB) + p(AB)

Или из определения условной вероятности

p(A) = p(A|B)*p(B) + p(A|B)*p(B)

3.2.4.2. Точные вероятностные рассуждения

Рассмотрим простейшую продукцию:

Если A, тоB.

Необходимо выяснить истинность B. Неопределенными могут быть два факта: посылкаA, истинность самой импликации.

Пусть мы на 90% уверены в истинности Aи на 95% уверены в том, что изAвсегда следуетB. Т.е.p(A) = 0.9,p(B|A) = 0.95.

Из правила композиции:

p(B) = p(B|A)*p(A) + p(B|A)*p(A)

Нам известны p(A) иp(B|A). Кроме того,p(A) = 1 -p(A).

В случае, если база знаний не содержит продукции "Если A, тоB" с указанием вероятности импликации, величинаp(B|A) остается неизвестной. Т.е., подставив известные величины, получаем

p(B) = 0.95*0.9 + p(B|A)*0.1 = 0.855 + p(B|A)*0.1

Откуда можно заключить лишь, что p(B) лежит в пределах от 0.855 до 0.955

Конъюнктивная посылка

Рассмотрим импликацию, в которой две посылки объединены с помощью правила И:

Если AИB, тоC.

Типичной ситуацией является наличие сведений о вероятности A,Bи импликации. Например,p(A) = 0.8,p(B) = 0.7,p(C|AB) = 0.95. Однако, записав при помощи правила композиции формулу для нахожденияp(C), мы видим, что данных недостаточно:

p(C) = p(C|AB)*p(AB) + p(C|~(AB))*p(~(AB))

Кроме того, в данной формуле отсутствуют p(A) иp(B). Существует методика оценкиp(AB) при известныхp(A) иp(B):

min {p(A), p(B)}  p(AB)  max{p(A) + p(B) – 1, 0}

Или в общем виде:

Дизъюнктивная посылка

Импликация, в которой посылки объединены по ИЛИ, менее жестка, чем предыдущая:

Если AИЛИB, тоC.

Вероятность можно оценить следующим образом:

Однако надежнее с теоретических позиций расписать формулу полной вероятности:

p(C) = p(C|AB)*p(AB) +

p(C|AB)*p(AB) +

p(C|AB)*p(AB) +

p(C|AB)*p(AB)

Отсюда видно, что для исчисления импликаций такого рода нужно обладать большим количеством информации, что не всегда возможно технически.

Из рассмотренных случаев можно заключить, что попытки в условиях неопределенности произвести точное вероятностное рассуждение часто (даже при незначительном возрастании сложности импликаций) приводят к приближенности. Основные два приема, которые можно рекомендовать для таких случаев:

1. При получении оценочного интервала для какой-либо величины брать среднее значение, либо проводить вычисление до конца, получая максимум и минимум всего выражения.

2. При наличии неизвестных величин типа p(C|AB) илиp(C|~(AB)) считать их равными 0 из логических соображений.

3.2.4.3. Приближенные вероятностные рассуждения

Как сказано выше, точные вероятностные рассуждения во многих случаях значительно менее применимы и надежны, чем приближенные. Рассмотрим схему приближенного рассуждения, использованную в ЭС MYCINиEMYCIN.

В этой схеме вместо вероятности использованы так называемые коэффициенты определенности. Если есть посылка A, импликацияABи заключениеB, то коэффициент определенности посылкиct(A) эквивалентен вероятности посылкиp(A), коэффициент определенности импликацииct(AB) эквивалентен условной вероятности заключения при истинности посылкиp(B|A), а коэффициент определенности заключения находится следующим образом:

ct(B) = ct(A)ct(AB)

Конъюнктивная посылка

Для конъюнкции посылок:

Коэффициент определенности конъюнкции посылок равен коэффициенту определенности наименее надежной из посылок:

Дизъюнктивная посылка

Для дизъюнкции посылок:

Коэффициент определенности дизъюнкции посылок равен коэффициенту определенности наиболее надежной из посылок:

Если сравнить эти формулы с формулами оценок вероятностей конъюнкций и дизъюнкций посылок для точных вероятностных рассуждений, то первую из них можно квалифицировать как оптимистическую, а вторую как пессимистическую. Коэффициент определенности заключения будет равен произведению коэффициента определенности логической комбинации посылок на коэффициент определенности импликации.

Как правило, посылки не формулируют в виде дизъюнкций. Импликацию с дизъюнкцией в посылке можно разбить на совокупность отдельных импликаций с указанием вероятностей для каждой посылки и импликации:

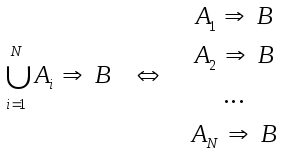
Решение о той или иной формулировке принимается экспертом в соответствии с его представлениями о данном правиле.

Поддержка одного заключения множеством правил

Если есть множество независимых правил с одним заключением:

,

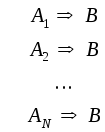то коэффициент определенности заключения ct_i(B) для каждого из этих правил находится независимо. Рассмотрим, как рассчитать единый коэффициент определенности заключения.

Для случая двух правил ct(B) =ct₁(B) +ct₂(B) -ct₁(B)*ct₂(B). Это выражение удачно иллюстрируется кругами Эйлера.

В общем случае:

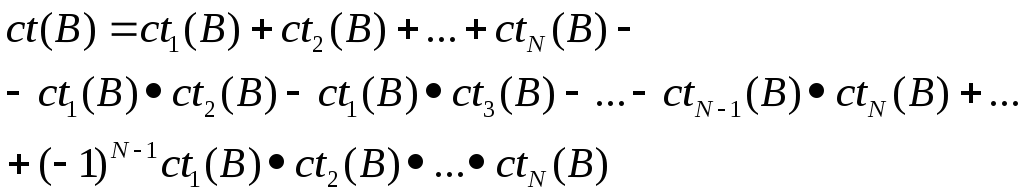
Это правило есть прямая аналогия правила И/ИЛИ.

Биполярные коэффициенты уверенности

В системе EMYCINиспользуется схема коэффициентов определенности с одним дополнением, а именно - с биполярностью. +1 обозначает полную уверенность, -1 - полную неверность заключения или посылки, 0 - отсутствие информации. Определенный положительный момент этой схемы состоит в том, что коэффициент определенности отрицания утверждения противоположен коэффициенту определенности утверждения. В этом случае вышеприведенные формулы преобразятся следующим образом:

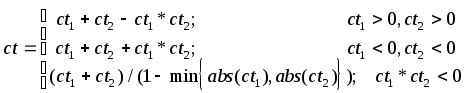
Недостатком схемы можно назвать тот факт, что коэффициенты определенности для большего числа посылок должны вычисляться рекуррентно через формулу для двух посылок.