
КМиИсО
.pdf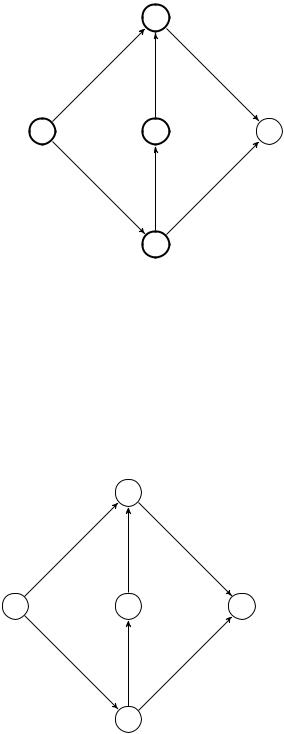
a (s+;3)
(5; 2) |
(2; 2) |
(1; 0)
(s+;1)
(4; 3)
(s+;1) s  b
b  t
t
(4; 4)
(1; 1)
(4; 4) |
(5; 3) |
d (b ;1)
ØÀÃ 5. . Óçåë t получает метку (d+; 2), поскольку является смежным с отмеченным и не просмотренным узлом d,(d; t) - äóãà, è f(d; t) = 3 < c(d; t) = 5: Определим путь P , увеличивающий поток. Так как
(b ; 1); b |
= |
(s+; 1), то имеем следующий увеличивающий (s; t)- ïóòü: |
s ! b |
d |
! t. На прямых дугах (s; b) è (d; t) этого пути увеличим |
поток на "t = 1, а на обратной дуге (d; b) уменьшим на 1. Мы получим новый, больший, чем исходный, поток.
|
a |
(5; 2) |
(2; 2) |
(1; 0)
(4; 4)
s  b
b  t
t
(4; 4)
(1; 0)
(4; 4) |
(5; 4) |
d
Попробуем опять увеличить поток.
31
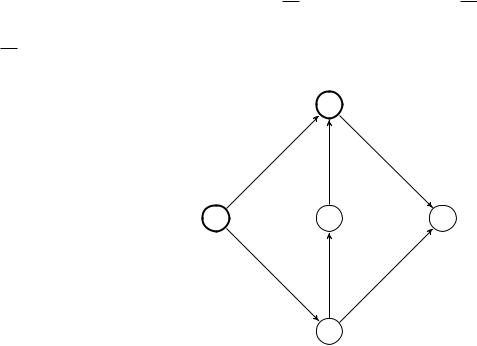
Отметим узел s - (s+; 1). Из узлов, соседних с s, можно отметить лишь узел a (s+; 3). Óçåë s переходит в множество просмотренных узлов.
Рассмотрим неотмеченные узлы, соседние с узлом a.
Óçåë t не отмечается, так как (a; t) - äóãà è f(a; t) = 2 = c(a; t):
Óçåë b не отмечается, так как (b; a) - äóãà è f(b; a) = 0:
Óçåë a переходит в множество просмотренных узлов. Поскольку в сети
нет отмеченных и не просмотренных узлов, то полученный поток является максимальным.
Определим минимальный разрез. Ко множеству X относятся все отмеченные узлы: X = fs; ag, ê X - все остальные: X = fb; d; tg. В разрез входят дуги, идущие из узлов множества X в узлы множества
X : (s; b); (s; d); (a; t):
a (s+;3)
(5; 2) |
(2; 2) |
(1; 0)
(4; 4)
(s+;1) s  b
b  t
t
(4; 4)
(1; 0)
(4; 4) |
(5; 4) |
d
Величина потока V = 10 равна суммарной пропускной способности дуг разреза.
Теорема 4.2 Если пропускные способности всех дуг сети рациональны и изначально в ней пропущен поток с рациональными значениями на всех дугах, то алгоритм Форда-Фалкерсона строит поток максимальной мощности за конечное число шагов.
32
Если в сети есть дуги с иррациональными пропускными способностями, то их можно заменить на чуть меньше рациональные и для новых пропускных способностей построить максимальный поток. Его мощность будет близка к максимальной мощности исходной сети, так как минимальная пропускная способность уменьшается на очень малую величину.
33
5Задача нахождения потока заданной мощности минимальной стоимости. Алгоритмы Басакера-Гоуэна и Клейна.
5.1Основные определения
Пусть снова задана сеть G = (V; E), в которой пропущен допустимый поток f. При этом, кроме пропускной способности каждой дуге поставлено в соответствие еще одно значение d(x; y)(любого знака), называемое стоимостью доставки единицы потока по дуге. Тогда каждой дуге e â ñåòè G будут соответствовать три значения: c(e); f(e); d(e): Обозначения рассмотрим на следующем примере.
5.2Пример
|
b |
|
|
3;2 |
|
5;3 |
|
1 |
|
2 |
|
a |
1;1 |
d |
|
1 |
|||
|
|
||
2;2 |
|
4;1 |
|
3 |
|
1 |
c
В этих обозначениях два числа над чертой обозначают соответственно пропускную способность дуги и мощность пропущенного по ней потока, а число под чертой - стоимость доставки единицы потока по дуге. Например, в дан-
íîé ñåòè äóãà (a; b) имеет пропускную способность 3, по ней пропущен поток мощности 2, а стоимость доставки единицы потока по данной дуге равна 1. Для дуги (c; b) и пропускная способность, и мощность, и стоимость одинаковы и равны 1.
Определение 5.1 Если в сети пропущен поток f, то стоимостью по-
34
тока называется число
|
X |
S(f) = |
d(x; y)f(x; y) |
|
(x;y)2E |
5.3Постановка задачи
Постановка задачи.
Пусть G = (V; E) - сеть, в которой для любой дуги (x; y) 2 E заданы пропускная способность c(x; y) 0 и стоимость d(x; y);. Среди допустимых потоков (то есть удовлетворяющих условиям
0 f(x; y) c(x; y); 8(x; y) 2 E)
заданной мощности
M(f) = ;
найти поток минимальной cтоимости S(f):
При этом подразумевается, что величина не превышает максимальной мощности допустимого потока из s â t, иначе задача не имеет решения.
5.4Пример
Вернемся к задаче о туристах предыдущего параграфа. Предположим, нам необходимо отправить именно сегодня группу всего из 25 туристов (так как они едут не на отдых и привязаны к конкретным срокам), но таким образом, чтобы суммарная стоимость всех билетов была минимальной, при условии, что цены на билеты, выраженные в некоторых условных единицах, на сегоднящние рейсы заданы.
Задачи такого типа решаются с помощью алгоритмов, созданных для нахождения оптимальных потоков заданной мощности. Два таких алгоритма и рассматриваются в настоящем параграфе.
В каждом из них существенную техническую роль играет так называемый граф модифицированных стоимостей Gf .
35
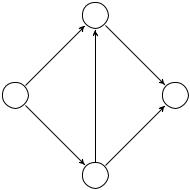
Пусть дана сеть G = (V; E), в которой пропущен допустимый поток f. Ãðàô Gf = (Vf ; Ef ) строится следующим образом: множество вершин совпа-
дает с множеством вершин графа G, ò.å. Vf = V ; множество Ef определяется правилами:
1.Åñëè (x; y) 2 E è f(x; y) = 0, то в графе Gf вводится одна дуга (x; y) 2 Ef , имеющая длину (модифицированную стоимость)
df (x; y) = d(x; y):
2. Åñëè (x; y) 2 E è f(x; y) = c(x; y), то в графе Gf задают одну дугу (y; x) 2 Ef , имеющую длину (модифицированную стоимость)
df (y; x) = d(x; y):
3. Åñëè (x; y) 2 E è 0 < f(x; y) < c(x; y), то в графе Gf
äóãè (x; y) 2 Ef è (y; x) 2 Ef , имеющие соответственно длины df (x; y) = d(x; y) è df (y; x) = d(x; y).
5.5Пример
f(ñì.
a |
1;1 |
d |
|
1 |
|||
|
|
где указанные над каждой дугой (x; y) числа c(x;y);f(x;y)
d(x;y) показывают соответственно пропускную способность, пропущенный поток и стоимость едини-
цы потока.
36
Тогда граф Gf = (V; Ef ) имеет вид:
|
|
b |
|
1 |
2 |
|
1 |
2 |
a |
1 |
d |
|
1
3
 1 c
1 c
Теорема 5.1 Поток мощности оптимален (то есть имеет минималь-
ную стоимость среди всех потоков сети, имеющих заданнную мощность) тогда и только тогда, когда граф модифицированных стоимостей Gf íå содержит ориентированных циклов отрицательной длины.
Для решения задачи о нахождении оптимального потока нужной мощности обычно используют один из двух следующих алгоритмов:
5.6Алгоритм Басакера-Гоуэна
ШАГ 0: Решение начинаем с нулевого потока M(f) = 0. Полагаем 0 = 0:
Пусть в сети пропущен поток f мощности M(f) < :
ШАГ 1: Строим граф модифицированных стоимостей Gf .
ШАГ 2: Если в графе модифицированных стоимостей Gf нет ни одной цепи из s â t è 0 < , то задача нахождения потока минимальной стоимости,
имеющего заданную мощность , не имеет решения. В исходной сети G пропущен поток максимальной мощности 0( 0 < ) минимальной стоимости.
Åñëè â Gf существуют пути из s â t, находим среди них кратчайший ïóòü P (роль длин дуг играют их модифицированные стоимости).
37
ШАГ 3: В исходном графе определяем элементарную (s; t) - öåïü P , соответствующую пути P . На прямых дугах цепи P вычисляем:
"1 = minfc(x; y) f(x; y)g;
на обратных -
"2 = minff(y; x)g:
Находим
" = minf"1; "2; 0g:
На прямых дугах пути P величину потока увеличиваем, а на обратных уменьшаем на ".
ШАГ 4: Полагаем
0 = 0 + ":
Åñëè 0 < , то переходим к Шагу 1; если 0 = , то алгоритм свою работу закончил, в сети построен оптимальный поток.
Теорема 5.2 Если в сети G нет циклов отрицательной стоимости, то алгоритм Басакера-Гоуэна на каждом шаге строит оптимальный поток.
Упражнение 1. Доказать, что если пропускные способности всех дуг рациональны, то алгоритм Басакера-Гоуэна строит решение за конечное число шагов.
Упражнение 2. Верен ли результат упражнения 1 в случае, когда пропускные способности дуг произвольны? Как можно решить задачу нахождения оптимального потока в этом случае?
5.7Пример
Построить поток заданной мощности = 3 минимальной стоимости в сети
G:
38
|
a |
|
|
4;0 |
|
2;0 |
|
5 |
|
1 |
|
s |
3;0 |
t |
|
1 |
|||
|
|
||
2;0 |
|
3;0 |
|
1 |
|
6 |
b
Итерация 1.
Полагаем 0 = 0. Строим граф модифицированных стоимостей Gf :
a
5  1
1
s |
1 |
t |
1  6 b
6 b
Находим кратчайший(наиболее дешевый) путь P èç s â t:
P : s ! b ! a ! t;
длина которого (модифицированная стоимость) равна 3. Соответствующая ей элементарная (s; t) - öåïü
P : s ! b ! a ! t
è
" = minf2; 3; 2g = 2:
Так как все дуги цепи - прямые, то увеличивая на пути P величину потока на 2, получаем
39

|
a |
|
|
4;0 |
|
2;2 |
|
5 |
|
1 |
|
s |
3;2 |
t |
|
1 |
|||
|
|
||
2;2 |
|
3;0 |
|
1 |
|
6 |
b
Пересчитываем
0 = 0 + " = 0 + 2 = 2:
Поскольку 0 < , то переходим к Шагу 1.
Итерация 2.
Строим граф модифицированных стоимостей Gf :
a
5 1
s |
1 |
1 t |
|
1 6
b
Находим в графе модифицированных стоимостей кратчайший путь
P : s ! a ! b ! t;
длина которой равна 10. Соответствующий ей (s; t) -ïóòü
P : s ! a b ! t
На прямых дугах пути P вычисляем:
"1 = minf4 0; 3 0g = 3;
на обратных -
40
