
metod_tau_kontr_rab
.pdfУДК 62-53.001 ББК 32.965я73 Б 53
Рекомендовано к опубликованию учебно-методическим управлением ГУВПО «Белорусско-Российский университет»
Одобрено кафедрой «Электропривод и автоматизация промышленных установок» XX xxxxx 2007 г., протокол №XX
Составители: канд. техн. наук, доц. кафедры «ЭП и АПУ» К.В.Овсянников канд. техн. наук, доц. С.В.Кольцов;
Рецензент канд. техн. наук, доц. С.К. Крутолевич
Методические указания по курсу «Теория автоматического управления» для студентов дневной и заочной форм обучения специальности 1-53 01 05 «Автоматизированный электропривод»
Учебное издание
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ ПО КУРСУ «ТАУ»
Ответственный за выпуск |
Г.С. Леневский |
Технический редактор |
А.А. Подошевко |
Компьютерная верстка |
Н.П. Полевничая |
Подписано в печать . Формат 60х84/16. Бумага офсетная. Гарнитура Courier New. Печать трафаретная.
Усл. печ. |
л. |
. Уч.-изд. л. |
. |
Тираж XXX |
экз. Заказ № |
|
|
Издатель и полиграфическое исполнение Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет» ЛИ № 02330/375 от 29.06.2004 г. 212005, г. Могилев, пр. Мира, 43
© ГУВПО «Белорусско-Российский университет», 2007

1. Теоретические сведения
1.1 Определение передаточных функций
X(p) |
Y(p) |
|
W(p) |
Рисунок 1.1 – Передаточная функция звена
Передаточная функция звена, изображенного на рисунке 1.1 будет равна отношению изображения Y(p) к изображению
X(p):
W ( p) = Y ( p)
X ( p)
В алгоритмических схемах автоматических систем встречаются три типа соединений динамических звеньев:
-последовательное; -параллельное;
-встречно-параллельное (соединение с обратной связью). Группу динамических звеньев, составляющих то или иное соединение, можно представить одним эквивалентным динамическим звеном, обладающим такими же статическими и динамическими характеристиками, что и замещаемое им соединение. Это позволяет упрощать алгоритмические схемы и выполнять их преобразования.
Последовательным называется такое соединение двух или нескольких звеньев, при котором выходная величина предыдущего звена является входной величиной для последующего (рисунок 1.1).
X(p) |
|
|
Y1(p) |
|
|
Y2(p) |
|
Y(p) |
|
W1(p) |
|
|
|
W2(p) |
|
Wk(p) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Рисунок 1.2 - Последовательное соединение звеньев
Из определения передаточной функции звена можно найти эквивалентную передаточную функцию:
W ( p) = YX ((pp)) ,
но:
Y1 ( p) = X ( p)×W1 ( p) Y2 ( p) = Y1 ( p)×W2 ( p)
...
Y ( p) = Yk −1 ( p)×Wk ( p)
Подставляя, получается:
W ( p) = W1 ( p) ×W2 ( p) ×...×Wk ( p)
Полученный результат говорит о том, что последовательное соединение звеньев эквивалентно одному звену, передаточная функция которого равна произведению передаточных функций последовательно соединенных звеньев.
Параллельным называется такое соединение двух или нескольких звеньев, при котором входная величина у всех звеньев одна и та же, а выходные величины складываются (рисунок 1.3).
|
|
|
|
Y1(p) |
|
|
|
W1(p) |
|
|
|
X(p) |
|
|
Y2(p) |
||
|
|
|
|||
|
|
|
|||
|
|
|
|
Y(p) |
|
|
|
W2(p) |
Yk(p) |
||
|
|
||||
|
|
|
|
||
|
|
|
|
||
|
|
Wk(p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.3 - Параллельное соединение звеньев
Из определения передаточной функции звена можно найти эквивалентную передаточную функцию:
W ( p) = Y ( p) X ( p)
Y ( p) = Y1 ( p)+Y2 ( p)+...+Yk ( p)
Y1 ( p) = X ( p)×W1 ( p) Y2 ( p) = X ( p)×W2 ( p)
...
Y ( p) = X ( p)×Wk ( p)
тогда:
W ( p) = Y ((p)) = Y1 ( p)+Y2 ( p()+)...+Yk ( p) = Y1 ((p)) + Y2 (( p)) +...+ Yk (( p)) =
X p X p X p X p X p =W1 ( p) +W2 ( p) +...+Wk ( p)
Отсюда следует, что параллельное соединение звеньев
эквивалентно одному звену, передаточная функция которого равна сумме передаточных функций параллельно соединенных звеньев.
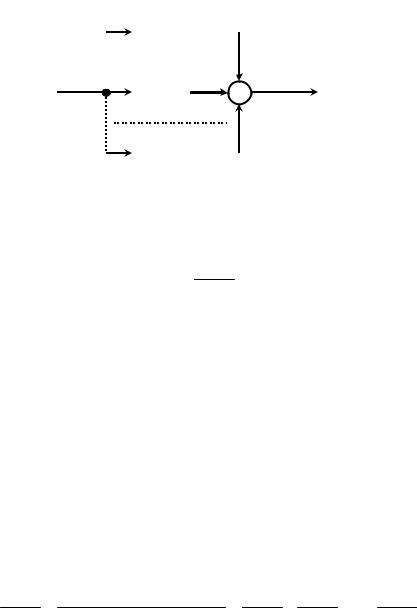
Встречно-параллельным называется такое соединение двух звеньев, при котором выходная величина одного звена подается обратно на его вход через другое звено (рисунок
1.4).
G(p) |
X(p) |
(-)
Yoc(p)
а)
Y(p) |
Wпр(p)
Wос(p) 
G(p) |
|
|
|
Y(p) |
|
Wпр(p) |
|||
|
|
|
||
|
|
1+Wпр(p)Wос(p) |
|
|
|
|
б) |
|
|
Рисунок 1.4 - Звено, охваченное обратной связью (а) и его эквивалентная структурная схема (б)
Встречно-параллельное соединение часто называется со-
единением с обратной связью. При этом звено, стоящее в прямой цепи (звено с передаточной функцией Wпр(p) является
звеном, охватываемым обратной связью, а звено, стоящее в цепи обратной связи (звено с передаточной функцией Wос(p)
— звеном в цепи обратной связи. Изображение выходной ве-
личины звена обратной связи Yос(p) вычитается из изображения входной величиной G(p) встречно-параллельного соединения или может складываться с ней. В первом случае имеет место отрицательная обратная связь, а во втором — положительная обратная связь.
При отрицательной обратной связи на вход звена, охватываемого обратной связью, поступает изображение сигнала X(p)=G(p)-Yос(p); при положительной обратной связи — сиг-
нал X(p)=G(p)+Yос(p).
Необходимо найти соотношение, связывающее изображения выходной Y(p), и входной G(p) величин встречнопараллельного соединения звеньев.
Изображение выходной величины:
Y ( p) = X ( p) ×Wпр ( p)
Для отрицательной обратной связи:
X ( p) = G ( p) -Yос ( p)
Так как:
Yос ( p) = Y ( p) ×Wос ( p) ,
то
X ( p) = G ( p) -Y ( p) ×Wос ( p)
Выразим X(p) через Y(p):
|
|
|
X ( p) = |
Y ( p) |
|
|
|
|
|
|
|
W ( p) |
|
|
|||
|
|
|
|
|
|
|||
Значит: |
|
|
пр |
|
|
|||
|
|
|
|
|
|
|||
|
Y ( p) |
= G ( p)-Y ( p)×W |
( p) |
|||||
Wпр ( p) |
||||||||
|
|
|
ос |
|
||||
|
|
|
|
|
||||
Отсюда |
|
Wпр ( p) |
|
|
||||
Y ( p) = |
|
×G ( p) |
||||||
1+W ( p)×W ( p) |
||||||||
|
|
|
пр |
ос |
|
|
||
или
Y ( p) = W ( p)×G ( p)
W ( p) = |
Wпр ( p) |
|
|
1+W |
( p)×W |
( p) |
|
|
пр |
ос |
|
Следовательно, звено с передаточной функцией Wпр(p), охваченное отрицательной обратной связью через звено с передаточной функцией Wос(p), в смысле прохождения сигнала эквивалентно одному звену, передаточная функция которого равна передаточной функции звена, охватываемого обратной связью, деленной на единицу плюс произведение передаточных функций звеньев, входящих в соединение (рисунок 1.4,
б).
При помощи аналогичных рассуждении нетрудно показать, что соотношение остается справедливым и для случая положительной обратной связи, при этом
W ( p) = |
Wпр ( p) |
|
|
1-W |
( p)×W |
( p) |
|
|
пр |
ос |
|
1.2 Передаточные функции САР
При исследовании и расчете систем автоматического управления исходят из математического описания происходящих в них физических процессов. Обычно это описание бывает представлено в виде системы дифференциальных уравнений, выражающих связи между переменными величинами и их производными. Такой подход, когда уравнения описывают поведение исследуемой системы в целом, является наиболее

общим в математическом плане и применимым во всех случаях.
В месте с тем для большого класса систем автоматического управления (линейных систем) широко применяется и другой способ, связанный с использованием операторного метода. При этом способе исследуемая система разделяется на части — звенья направленного действия, обладающие свойством передачи сигнала только в одном направлении: от входа к выходу. Совокупность этих звеньев совместно с линиями связи между ними, характеризующими их взаимодействие, образует структурную схему системы управления. При таком начертании структурная схема САР представляет собой графическое изображение системы дифференциальных уравнений, описывающих работу САР. Графическое изображение уравнений звеньев предпочтительнее обычной математической записи этих уравнений. При этом для разделения систем управления на звенья направленного действия нельзя дать какого-то единого рецепта, а приходится каждый раз руководствоваться в значительной мере соображениями общего порядка и интуицией, приобретаемыми в процессе накопления опыта. Разбивать САР на звенья можно различным образом. Желательно разбивать САР на типовые звенья направленного действия, уравнения которых известны. Часто в качестве динамических звеньев выбирают просто элементы САР.
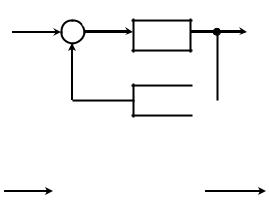
После того как получены передаточные функции входящих в нее звеньев и составлена структурная схема, необходимо определить передаточные функции всей системы. Для этого структурная схема любой САР может быть приведена к виду, показанному на рисунке 1.5.
|
|
F(p) |
G(p) |
X(p) |
Y(p) |
|
||
|
W1(p) |
W2(p) |
≈ |
(-) |
|
|
Yос(p) |
|
|
|
Wос(p) |
Рисунок 1.5 - Структурная схема одноконтурной CAP
На этом рисунке для упрощения показано лишь одно возмущающее воздействие F(p), приложенное к объекту регулирования. В общем случае число возмущающих воздействий может быть любым.
Для расчетов обычно необходимы передаточные функции:

-разомкнутой CAP W(p);
-передаточная функция замкнутой CAP относительно задающего воздействия Φ(p);
-передаточная функция замкнутой CAP относительно возмущения Φf(p);
-передаточная функция замкнутой CAP для ошибки воспроизведения задания Φx(p);
-передаточная функция замкнутой CAP для ошибки от возмущающего воздействия Φxf(p).
Определим, что представляют собой эти передаточные функции, и найдем их значения для одноконтурной CAP (рисунок 1.5)
Передаточная функция разомкнутой CAP:
W ( p) = Yос ( p) G ( p)
есть отношение изображения Yос(p) сигнала обратной связи yос(t) к изображению G(p) задающего воздействия g(t) (все возмущающие воздействия при этом считаются равными нулю). Контур регулирования считают разомкнутым около элемента сравнения, как показано на рисунке 1.5 волнистыми линиями.
Передаточная функция замкнутой CAP относительно задающего воздействия есть отношение изображения Y(p) регулируемой величины к изображению задающего воздействия G(p) при этом предполагается, что других внешних воздействий нет:
Ф ( p) = Y ( p)
G ( p)
Для CAP со структурной схемой, изображенной на рисун-
ке 1.5,
Ф ( p) = |
|
W1 ( p)×W2 ( p) |
|
|
1+W |
( p)×W |
( p)×W |
( p) |
|
1 |
2 |
ос |
|
|
Передаточная функция Φ(p), которую еще называют главным оператором системы, характеризует передачу системой задающего воздействия, его воспроизведение регулируемой величиной. Воспроизведение тем лучше, чем ближе зна-
1
чение Φ(p) к идеальному: Φ(p)=Wос(p).
Передаточная функция замкнутой CAP для ошибки воспроизведения задания
Ф( p) = X ( p)
xG ( p)
есть отношение изображения X(p) рассогласования X(p)=G(p)—Yос(p), к изображению задающего воздействия при отсутствии других внешних воздействий.

У рассматриваемой системы
Фx ( p) = |
|
|
|
1 |
|
1 |
+W1 |
( p)×W2 ( p)×Wос ( p) |
|||
|
|||||
Передаточная функция Φx(p), как и Φ(p) характеризует
воспроизведение регулируемой величиной задающего воздействия (отработку задания). Воспроизведение тем лучше, чем
ближе значение Φx(p) к идеальному: Φx(p)=0.
Передаточная функция замкнутой CAP относительно возмущения
Фf ( p) = |
Y ( p) |
|
F ( p) |
||
|
есть отношение изображения Y(p) регулируемой величины к изображению F(p) возмущения. При этом предполагают, что других внешних воздействий нет.
Для рассматриваемой системы
Фf ( p) = |
|
|
|
W2 ( p) |
|
1 |
+W1 |
( p)×W2 ( p)×Wос ( p) |
|||
|
|||||
Передаточная функция Φf(p) показывает влияние возму-
щения f(t) на регулируемую величину y(t). Возмущение стремится отклонить ее от заданного значения и уменьшает точность воспроизведения задающего воздействия. Это вредное влияние возмущения тем меньше, чем ближе значение Φf(p) к идеальному: Φf(p)=0.
Если на систему воздействует несколько возмущений f1,f2,...fn, то определяются передаточные функции Φ1f(p), Φ2f(p)...Φnf(p) относительно каждого из них.
Передаточная функция замкнутой CAP для ошибки от возмущающего воздействия
Фxf ( p) = X ( p)
F ( p)
есть отношение изображения X(p) ошибки x(t)=g(t)—yос(t), к изображению возмущающего воздействия при отсутствии других внешних воздействий.
У рассматриваемой системы
Фxf ( p) = |
|
|
-W2 ( p)×Wос ( p) |
|
1 |
+W1 ( p)×W2 ( p)×Wос ( p) |
|||
|
||||
Передаточная функция Φxf(p) характеризует влияние возмущения на величину ошибки. В идеале: Φxf(p)=0.
1.3 Устойчивость САР
Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.
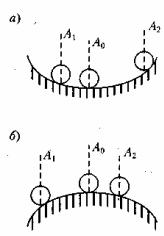
Иллюстрация понятия устойчивости приведена на рисунке 1.6. Состояние равновесия шара в точке А0 на рисунке 1.6, а) устойчиво, так как если какие-либо внешние силы выведут шар из этого состояния (например, в точку А1 или А2), то он возвратится к точке А0. Состояние равновесия в точке А0 на рисунке 1.6, б) неустойчиво.
Рисунок 1.6 – Понятие устойчивости
В этом примере, как и в теории устойчивости, полагается, что внешние силы или возмущения прекращают свое действие к некоторому моменту времени, который можно принять за начальный момент t = 0.
Автоматические системы отличаются тем, что в них, осуществляется специально организованное управление объектом. Благодаря ему система с неустойчивым объектом мо-
жет стать устойчивой, а |
система |
с устойчивым |
объектом |
(при неправильном управлении) — неустойчивой. |
была соз- |
||
Строгая математическая |
теория |
устойчивости |
|
дана А. И. Ляпуновым и изложена им в работе «Общая задача об устойчивости движения», опубликованной в 1892 г. В ней было определено понятие устойчивости и разработаны методы устойчивости нелинейных систем.
Математический признак устойчивости. САУ называется устойчивой, если она, будучи выведена из состояния равновесия и в дальнейшем не подвергаясь никаким внешним воздействиям, с течением времени стремится вернуться в прежнее состояние равновесия.
САУ, как любая динамическая система, характеризуется переходным процессом, возникающим в ней при нарушении ее равновесия каким – либо воздействием (могут быть сигналы управления, настройки, помехи и т.д.).
Переходный процесс y(t) зависит от свойств системы, так и от вида возмущения
Характер свободного движения системы определяет ее устойчивость или неустойчивость.
Первая теорема А.М. Ляпунова:
1.Для обеспечения устойчивости САУ, описываемой линейными дифференциальными уравнениями с постоянными коэффициентами, необходимо и достаточно, чтобы вещественные корни характеристического уравнения, соответствующего исходному дифференциальному уравнению, были отрицательными,
акомплексные корни имели отрицательную вещественную часть.
2.Если вещественная часть корней меньше нуля, но среди корней имеются нулевые или чисто мнимые корни, то система стремится к некоторому установившемуся процессу (консервативная система).
3.Если хотя бы один вещественный корень положительный или положительна вещественная часть хотя бы одного комплексного корня, то система неустойчива.
Поэтому вид кривой yC (t)определяется видом корней характеристического уравнения.
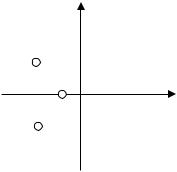
Im |
Система устойчива |
Re
Рисунок 1.7 – Распределение корней устойчивой системы
Критерии оценки устойчивости линейных САУ
Прямой метод анализа устойчивости систем, основанный на вычислении корней характеристического уравнения очень сложен, особенно для уравнений высоких степеней. Поэтому в инженерной практике используют методы, которые позволяют определять устойчивость системы без вычисления корней.
Эти методы называются критериями устойчивости. С помощью критериев устойчивости можно не только установить, является ли система устойчивой или нет, но и выяснить, как влияют на устойчивость те или иные параметры и структурные изменения в системе.
Различают две группы критериев устойчивости: алгебраические (Рауса и Гурвица), основанные на анализе коэффициентов характеристического уравнения и частотные (Михайлова и Найквиста), основанные на анализе частотных характеристик. Частотные критерии позволяют оценивать устойчивость системы, даже если в наличии имеются экспериментальные частотные характеристики, а уравнения динамики неизвестны.
