4 ЛинейныЕ экономико-математическиЕ моделИ

Пример задачи линейной модели

Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (см. табл.). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида. Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.

Таблица 1.1

Решение

Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены?

Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.

Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.

Построим модель задачи.

Переменные задачи

В задаче требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:

x1 – суточный объем производства краски 1-го вида, [т краски/сутки];

x2 – суточный объем производства краски 2-го вида, [т краски/сутки].

Целевая функция

В условии задачи сформулирована цель – добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи красок обоих видов, необходимо знать объемы производства красок, т.е. x1 и x2 т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов – согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен 3 x₁ тыс. руб. в сутки, а от продажи краски 2-го вида – 2x₂ тыс. руб. в сутки. Поэтому запишем целевую функцию в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)

Ограничения

Возможные объемы производства красок x1 и x2 ограничиваются следующими условиями:

• количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;

• согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;

• объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;

• объемы производства красок не могут быть отрицательными.

Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:

1) расходом ингредиентов;

2) рыночным спросом на краску;

3) неотрицательностью объемов производства.

Запишем эти ограничения в математической форме.

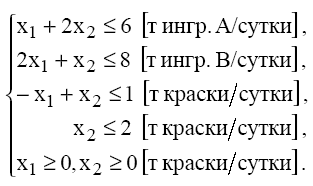
Таким образом, математическая модель задачи имеет вид:

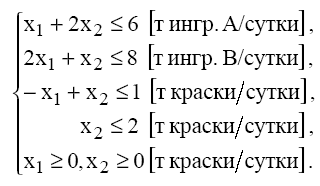
Формы записи задачи линейного программирования, их эквивалентность и способы преобразования

Модель задачи линейного программирования может быть записана в одной из приведенных ниже форм:

1. Общая, или произвольная, форма записи:

max(min)Z=

п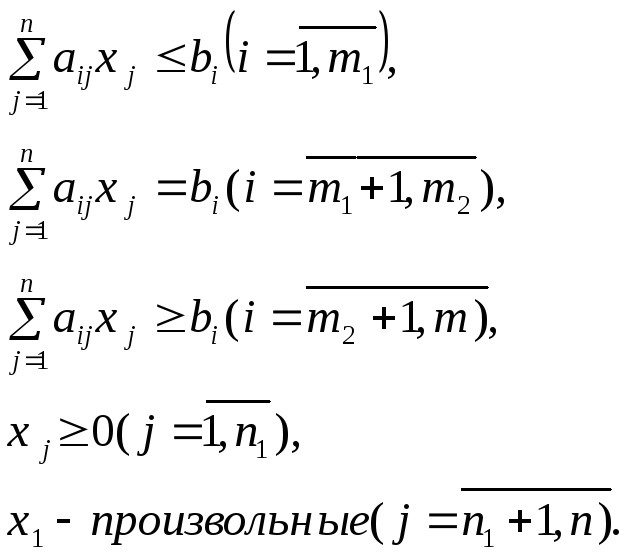ри ограничениях:

2.Симметричная, или стандартная, форма записи:

maxZ= minZ=

3.Каноническая, или основная, форма записи:

maxZ=

Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме, т.е. если имеется способ нахождения оптимального решения задачи в одной из указанных форм, то тем самым может быть определен оптимальный план задачи в любой другой форме (говорят о стратегической эквивалентности задачи в любой из форм).

Так, при необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Очевидно, что минимальное значение функции z(x) равно максимальному значению функции- z(x), взятому с противоположным знаком, т.е.

min z(x)=-max(-z(x)).

Неравенство типа > путем умножения левых и правых частей на -1 можно превратить в неравенство типа <, и наоборот. Ограничения-неравенства

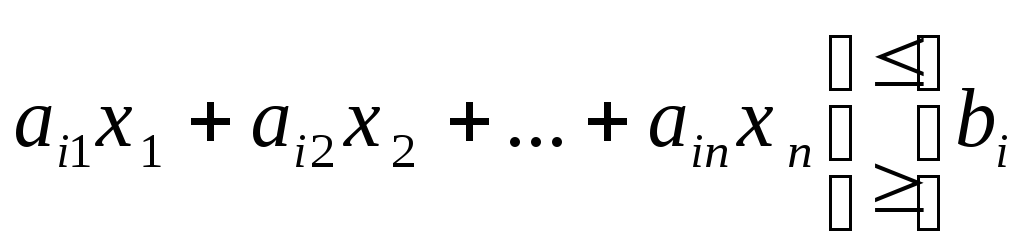
преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных x_n+i>0:

В случае необходимости ограничение-равенство

можно записать в виде системы неравенств

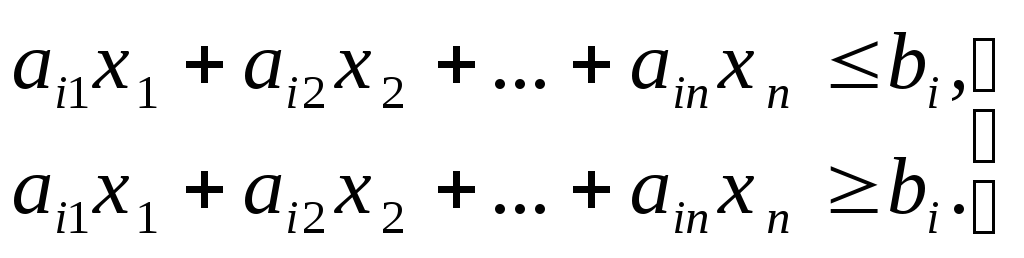
Если в ЗЛП какая-то переменная x_kне подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных х'_k>0 и х"_k>0:

x_k= х'_k - х"_k.

Решение прикладных задач средствами Excel

Для решения задач оптимизации в Excel существует мощный инструмент «Поиск решения» (Оптимизатор). Задачи, решаемые с помощью оптимизатора, имеют три характерных признака:

• Имеется единственная целевая ячейка. В нее пользователь должен ввести формулу, указав позднее в программном диалоге какой экстремум необходим (максимум или минимум). После завершения построения модели и инициализации расчета программа автоматически должна добиться для этой ячейки экстремального результата.

• В формуле целевой ячейки должны быть сделаны ссылки на одну или более изменяемых ячеек, от значений которых зависит результат. Они могут быть названы также неизвестными или переменными для решения. Поиск решения устанавливает значения изменяемых ячеек так, чтобы найти для формулы целевой ячейки оптимальное решение.

• Ограничивающих ячеек может быть не менее одной на каждую изменяемую ячейку. Может существовать и некоторое количество дополнительных ячеек ограничений, например, ограничение по объему ресурса и ограничения по спросу (минимальный спрос, максимальный спрос).

Элементы диалогового окна Поиск решения

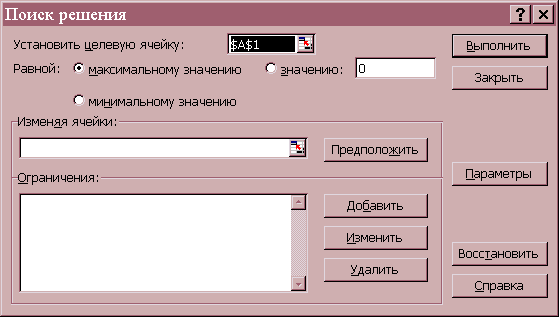
Рисунок 1 - Диалоговое окно Поиск решения

Рассмотрим элементы диалогового окна Поиск решения. Для этого зайдем в Сервис, Поиск решения. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для установки необходимо выполнить команду Сервис, Надстройки, Поиск решения.

После этого выберем команду Сервис, Поиск решения и заполняем открывшееся диалоговое окно Поиск решения следующим образом. В поле Установить целевую ячейку диалогового окна Поиск решения дается ссылка на ячейку с функцией, для которой будет находится максимум, минимум или заданное значение.

Тип взаимосвязи между решением и целевой ячейкой задается путем установки переключателя в группе Равной. Для нахождения максимального или минимального значения целевой функции этот переключатель ставится в положении Максимальному значению или Минимальному значению, соответственно. Для нахождения значения целевой функции, заданного в поле группы Равной, переключатель ставится в положение Значению.

В поле Изменяя ячейки указываются ячейки, которые должны изменяться в процессе поиска решения задачи, т.е. ячейки отведенные под переменные задачи.

Ограничения, налагаемые на переменные задачи, отображаются в поле Ограничения. Средство поиска решений допускает ограничения в виде равенств, неравенств, а также позволяет ввести требования целочисленности переменных. Ограничения добавляются по одному. Для ввода ограничений нажмите кнопку Добавить в диалоговом окне Поиск решения и в открывшемся диалоговом окне Добавления ограничения заполните поля.

Далее нажав кнопку Добавить в диалоговом окне Добавление ограничения, введите вторую группу ограничений, налагаемых на переменные, если это необходимо. Нажатие кнопки OK завершает ввод ограничений. Обратите внимание на то, что ограничения удобнее задавать в виде диапазонов.

Пример

Фирма производит и продает столы и шкафы из древесины хвойных и лиственных пород. Расход каждого вида в кубометрах на каждое изделие задан в таблице.

	Расход древесины, м3		Цена изделия, тыс. руб.
	хвойные	лиственные
Стол	0,15	0,2	0,8
Шкаф	0,3	0,1	1,5
Запасы древесины	80	40

Определить оптимальное количество столов и шкафов, которое следует поставлять на продажу для получения максимального дохода фирмы.

Решение

Обозначим через х1 – количество столов, х2 – количество шкафов.

Целевая функция имеет вид f = 0,8*х1 + 1,5*х2  max

Система ограничений:

0,15*х1 + 0,3*х2  80

0,2*х1 + 0,1*х2  40

х1, х2>=0

Решение задачи в Excel:

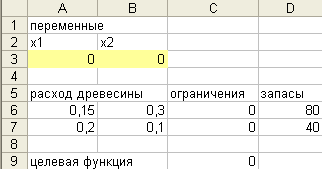
В ячейки А3:В3 будет помещен результат, в ячейках А6:В7 записаны коэффициенты технологической матрицы, в ячейки С6:С7 занесены ограничения, в ячейки D6:D7 занесены имеющиеся запасы.

Введенные зависимости представлены на рисунке:

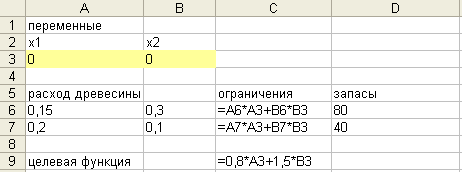
В диалоговом окне Поиск решения в поле Установить целевую ячейку вводим ячейку С9, устанавливаем переключатель Равной в положение «максимальному значению», в поле Изменяя ячейки вводим диапазон ячеек А3:В3, в поле Ограничения вводим ограничения:

C6<=D6

C7<=D7

A3:B3>=0

A3:B3 = цел

После нажатия кнопки Выполнить получаем ответ, представленный на рисунке.

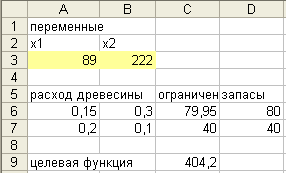
Ответ: следует выпускать 89 стульев и 222 шкафа.

Транспортная задача

Транспортная задача (ТЗ) формулируется следующим об­разом. В m пунктах отправления А1,... , Аm сосредоточен од­нородный груз в количествах соответственно а1,... , аm еди­ниц. Имеющийся груз необходимо доставить потребителям B1, ... , Вn, спрос которых выражается величинами b1 ... , bп единиц. Известна стоимость Cij перевозки единицы груза из i-го (i= 1,m) пункта отправления в j-й (j = 1,n) пункт на­значения. Требуется составить план перевозок, который пол­ностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются.

Условие транспортной задачи обычно записывается в виде матрицы, в которой потребители однородного груза размещаются по столбцам, а поставщики - по строкам. В последнем столбце матрицы проставляют запас груза, имеющийся у каждого поставщика, а в последней строке - потребность в нем потребителей. На пересечении строк со столбцами (в клетках матрицы) записывают размер поставки, а также расстояние пробега по всем возможным маршрутам, время доставки груза или затраты на перевозку единицы груза по этим маршрутам.

Потребители
Поставщики		П1	П2	...	Пj	...	Пn	Запас
	П1	c11	c12	...	c1j	...	c1n	а1
	П2	c21	c22	...	c2j	...	c2n	а2
	...	...	...	...	...	...	...	...
	Пi	ci1	ci2	...	cij	...	cin	аi
	...	...	...	...	...	...	...	...
	Пm	cm1	cm2	...	cmj	...	cmn	аm
	Спрос	b1	b2		bj	...	bn

Транспортная задача, для которой выполняется условие

называется закрытой, а в противном случае открытой.

Запишем математическую модель закрытой транспортной задачи (запас груза у поставщиков должен равняться суммарному спросу потребителей):

1) объем поставок i-гo поставщика должен равняться количеству имеющегося у него груза:

2) объем поставок j-му потребителю должен быть равен его спросу:

3) размер поставок должен выражаться неотрицательным числом:

4) общая сумма затрат на перевозку груза должна быть минимальной:

Математическая модель открытой транспортной задачи

Запас груза у поставщиков больше суммарного спроса потребителей	Запас груза у поставщиков меньше суммарного спроса потребителей
Ограничения на поставщиков:	Ограничения на поставщиков:
Ограничения на потребителей:	Ограничения на потребителей:

Пример

Найти решение транспортной задачи, исходные данные которой приведены в таблице

Пункты отправления	Пункты назначения						Запасы
	В1	В2	В3	В4
А1 А2 А3	30 40 50	50 50 10	62 80 30	10 20 30			650 850 700
Потребности	500	800	300	600

Решение

В ячейки B3:E5 введем технологическую матрицу, в ячейки B10:E12 – план перевозок (ответ), в ячейки G10:G12 – запасы, в ячейки B14:E14 – потребности, в ячейки F10:F12 – суммы перевозок по каждому пункту отправления, формулы имеют вид:

=СУММ(B10:E10)

=СУММ(B11:E11)

=СУММ(B12:E12)

В ячейки B13:E13 введены суммы перевозок по каждому пункту назначения:

=СУММ(B10:B12)

=СУММ(С10:С12)

=СУММ(D10:D12)

В ячейку С16 введена целевая функция, формула которой имеет вид

=СУММПРОИЗВ(B3:E5;B10:E12).

В диалоговом окне Поиск решения в поле Установить целевую ячейку вводим ячейку С16, устанавливаем переключатель Равной в положение «минимальному значению», в поле Изменяя ячейки вводим диапазон ячеек В10:E12, в поле Ограничения вводим ограничения:

F10=G10

F11=G11

F12=G10

B13=B14

C13=C14

D13=D14

E13=E14

B10:E12=цел

B10:E12>=0

После нажатия кнопки Выполнить получаем ответ, представленный на рисунке.

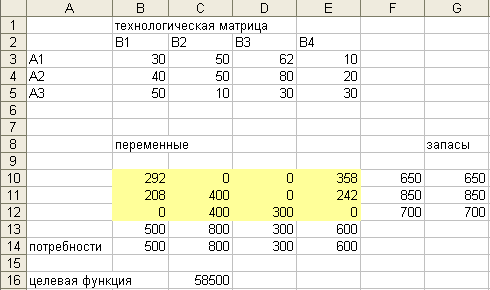
Транспортная задача с дополнительными ограничениями

а) Обязательные поставки. Дана транспортная следующая таблица

Таблица 3

Пусть, в силу определенных обстоятельств (например, госзаказ), третий поставщик А₃, несмотря на фактические затраты, обязан поставить четвертому потребителю В₄ не менее 100 единиц продукции.

В этом случае на соответствующую поставку вводят дополнительное ограничение: x₃₄ >100. При решении задачи в Excel данное ограничение вводят для соответствующей ячейки.

б) Запрет на перевозку. Запрет перевозок при решении транспортной задачи достигается за счет введения стоимости перевозки единицы груза c_ij намного большей, чем стои­мость остальных перевозок. Например, если по каким-то соображениям не­обходимо запретить перевозку от 1-го поставщика к 1-му по­требителю, то вместо тарифа на перевозку с₁₁ исходной транспортной задачи следует записать некоторое большое число М, которое намного превышает наиболь­шую стоимость перевозки груза. Так как задача решается на минимум функции, а стоимость с₁₁ довольно высокая, то в оптимальном плане объем перевозки х_ij будет равен нулю.

Если же при решении транспортной задачи все-таки окажется, что запре­щенная перевозка отлична от нуля при достаточно высокой стоимости перевозки груза в данной клетке, то это значит, что спрос j-го потребителя невоз­можно удовлетворить без i-го поставщика.

в) Задача с ограниченной пропускной способностью. Пусть в исходной задаче, приведенной в таблице 3, в силу некоторых обстоятельств по каналу А₂-В₁, несмотря на низкую стоимость перевозок, можно поставить не более 125 единиц продукции.

В этом случае на соответствующую поставку вводят дополнительное ограничение: x₂₁ <125. При решении задачи в Excel данное ограничение вводят для соответствующей ячейки.

г) Задача с фиксированной поставкой. Пусть объем d_ij поставки груза от i-го поставщика к j-му потребителю должен быть строго определенным . Эту поставку следует включить в опти­мальный план даже в том случае, если она невыгодна.

В этом случае на соответствующую поставку вводят дополнительное ограничение: x_ij = d_ij. При решении задачи в Excel данное ограничение вводят для соответствующей ячейки.

Транспортная задача с промежуточными пунктами.

Одно практически важное обобщение классической транспортной задачи связано с учетом возможности доставки товара от i-го поставщика к j-му потребителю по маршруту, проходящему через некоторый промежуточный пункт (склад). Так, например, промежуточные пункты являются составной частью распределительной системы любой крупной компании, имеющей сеть магазинов во многих городах. Такая компания обычно имеет зональные оптовые базы (поставщики, источники), снабжающие товарами более мелкие региональные склады (промежуточные пункты), откуда эти товары поступают в розничную торговую сеть (потребители, стоки). При этом товар для каждого фиксированного стока в общем случае может быть доставлен не из любого источника и по маршрутам, не обязательно проходящим через все промежуточные пункты. Кроме того, промежуточные пункты могут обладать вполне определенной спецификой. Так, например, при транспортировке товара от источника к стоку по маршруту, проходящему через склад, часть товара может быть использована для создания неприкосновенного запаса на складе.

Пример

Предположим, торговая фирма имеет восемь складов, на которых сосредоточены все имеющиеся в наличии запасы товара. Перед началом рекламной компании решено перераспределить часть запасов товара между складами в соответствии с прогнозами сбыта в районах их размещения. Требуется разработать план перевозок товара между складами, который позволит при минимальных транспортных затратах создать на каждом складе необходимый запас товара.

Решение

На рис. 8 представлена схема размещения складов, на которой указаны:

а) склады в виде узлов сети с номерами от 1 до 8;

б) избыток товара на складе, который должен быть перераспределен в системе складов (указан в квадратных скобках рядом с узлом сети положительным числом и выражен в единицах измерения товара);

в) недостаток товара на складе, который должен быть устранен за счет его поставок с других складов системы (указан в квадратных скобках рядом с узлом сети отрицательным числом);

г) возможность перевозки товара со склада i на склад j (ориентированная дуга от круга с номером i к кругу с номером j);

д) затраты, связанные с перевозкой единицы товара со склада i на склад j (величина c_ij рядом с соответствующей ориентированной дугой, выраженная в денежных единицах).

Рис. 8.

На рис 8 видно, что суммарный избыток товара, имеющийся на складах системы с номерами 1 и 4, равен суммарному недостатку товара, имеющемуся на складах с номерами 3, 6 и 8 той же системы. Перераспределение товара может происходить через склады с номерами 2, 4-7, которые в рассматриваемой задаче и являются промежуточными или транзитными пунктами. Истинным пунктом отправления является лишь склад с номером 1, на котором имеется избыток товара и с которого товар можно только вывозить, а истинными пунктами назначения являются склады с номерами 3 и 8, на которых есть недостаток товара, и на эти склады товары можно только завозить. Заметим также, что между складами с номерами 4 и 5 возможны перевозки в обоих направлениях, но в общем случае c₄₅c₅₄ (например, наличие одностороннего движения по кратчайшему маршруту). Объемы спроса и предложения, соответствующие этим пунктам отправления и назначения, вычисляются следующим образом:

Объем предложения истинного пункта отправления = объем исходного предложения.

Объем предложения транзитного пункта = объем исходного предложения + объем буфера.

Объем спроса истинного пункта назначения = объем исходного спроса.

Объем спроса транзитного пункта = объем исходного спроса + объем буфера.

Объем буфера должен быть таким, чтобы вместить объем всего предложения (или спроса).

Пусть J — множество номеров складов, на которые товар может быть доставлен с k-го склада, а I — множество номеров складов, с которых товар может быть доставлен на k-й склад. T_k — величина чистого запаса товара, равная объему исходного предложения или исходного спроса. Тогда математическую модель данной задачи можно представить следующим образом:

В специальной литературе по исследованию операций¹ приводится доказательство того, что рассматриваемая транспортная задача с промежуточными пунктами эквивалентна классической транспортной задаче.

Решение транспортной задачи с промежуточными пунктами в Excel

Рассмотрим методику решения в Excel транспортной задачи с промежуточными пунктами.

Условие. Найти решение транспортной задачи с промежуточными пунктами, в рассмотренном выше примере, если стоимость перевозки единицы товара составляет: c₁₂=3 у.е., c₂₃=7 у.е., c₂₅=3 у.е., c₄₃=6 у.е., c₄₅=4 у.е., c₄₇=5 у.е., c₅₄=5 у.е., c₅₆=3 у.е., c₆₇=5 у.е., c₇₈=2 у.е.

На рис. 9 представлены таблицы Стоимость перевозки единицы товара и План перевозок товара между складами, сформированные на рабочем листе Excel. Здесь в таблице Стоимость перевозки единицы товара мы видим, что если между отдельными складами отсутствует возможность перевозки товара, то в соответствующие ячейки таблицы (выделенные темным фоном) заносится любое большое число (в данном случае 100). Для того, чтобы найти в таблице Плана перевозок товара между складами объем предложения и объем спроса, определим объем буфера B по следующему правилу:

B = общий объем предложения = S₁+S₄= 10+2 = 12 ед.

или

B = общий объем спроса = D₃+D₆+D₈= 3+1+8 = 12 ед.

Для остальных промежуточных пунктов объемы предложения S_i или объемы спроса D_j равны нулю (см. рис. 9).

Рис. 9.

В целевую ячейку, в данном случае C23, необходимо занести формулу: =СУММПРОИЗВ(C4:I9;C15:I20).

Используя меню СервисПоиск решения открываем диалоговое окно Поиск решения (см. рис. 10), в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить.

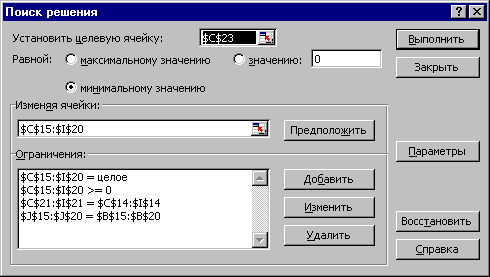
Рис. 10

Результат решения данной задачи представлен на рис. 11.

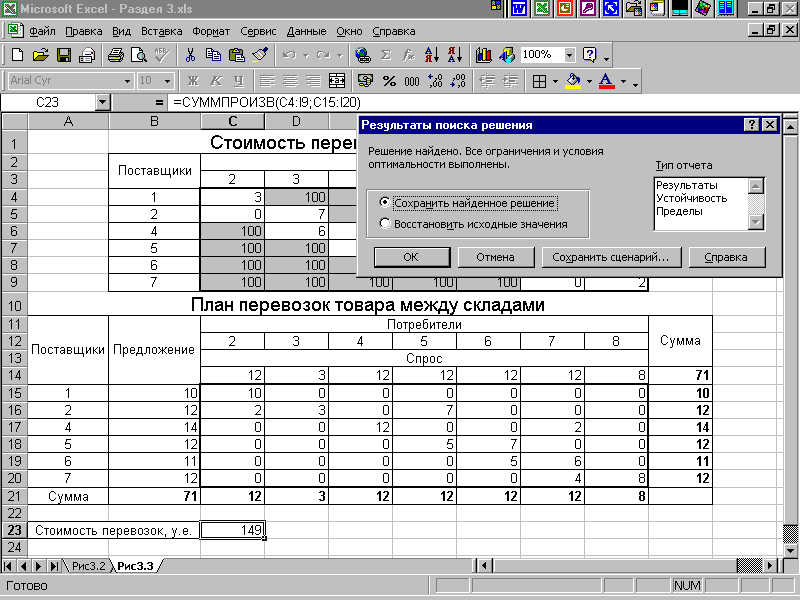
Рис. 11.

Здесь мы видим, что оптимальный план перевозок товара между складами следующий:

• со склада 1 товар в количестве трех единиц транзитом через склад 2 отправлен на склад 3, который является истинным пунктом назначения;

• со склада 1 товар в количестве семи единиц транзитом через склады 2 и 5 отправлен на склад 6, где одна единица товара используется для пополнения запаса на этом складе;

• со склада 6 товар в количестве шести единиц транзитом через склад 7 отправлен на склад 8, который также является истинным пунктом назначения;

• со склада 4 избыток товара в количестве четырех единиц отправлен на склад 8 транзитом через склад 7.

Стоимость перевозок при этом минимальна и составляет 149 условных денежных единиц.

Двойственность в задачах линейного программирования

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной, или прямой.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Хорошо разработанный математический аппарат линейного программирования позволяет не только получать с помощью эффективных вычислительных процедур оптимальный план, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, двойственной к исходной ЗЛП. Переменные двойственной задачи у_i называют объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми ценами.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Задача двойственная к исходной задаче строится по следующим правилам:

1. упорядочивается запись исходной задачи, т. е. если целевая функция задачи максимизируется, то ограничения-неравенства должны быть вида , если минимизируется, то вида ≥ . Выполнение этих условий достигается умножением соответствующих ограничений на -1;

2. матрица А, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица А^Т в двойственной задаче получаются друг из друга транспонированием.

3. число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи - числу переменных в исходной задаче.

4. коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи - коэффициенты при неизвестных в целевой функции исходной задачи.

5. каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства, соответствует переменная, связанная с условием неотрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.

Дадим экономическую интерпретацию пары двойственных задач.

Рассмотрим задачу рационального использования ресурсов. Пусть предприятие располагает ресурсами , которые могут использоваться для выпуска n видов продукции. Пусть также известны стоимость единицы j-го вида продукции и норма потребленияi-го ресурса на производство единицы j-й продукции — а_ij.

Требуется определить объем производства продукции каждого вида , максимизирующий суммарную стоимость

При этом расход ресурсов не должен превышать их наличия:

Все неизвестные по своему экономическому смыслу неотрицательны:

По исходным данным сформулируем другую экономическую задачу (двойственную).

Предположим, что некоторая организация может закупить все ресурсы, которыми располагает предприятие. Необходимо определить оптимальные цены (оценки) на эти ресурсы исходя из естественного условия, что покупающая организация стремится минимизировать общую оценку ресурсов. Нужно, однако, учитывать и тот факт, что за ресурсы покупающая организация должна уплатить сумму, не меньшую той, которую может выручить предприятие при организации собственного производства продукции.

Математическая модель задачи имеет вид

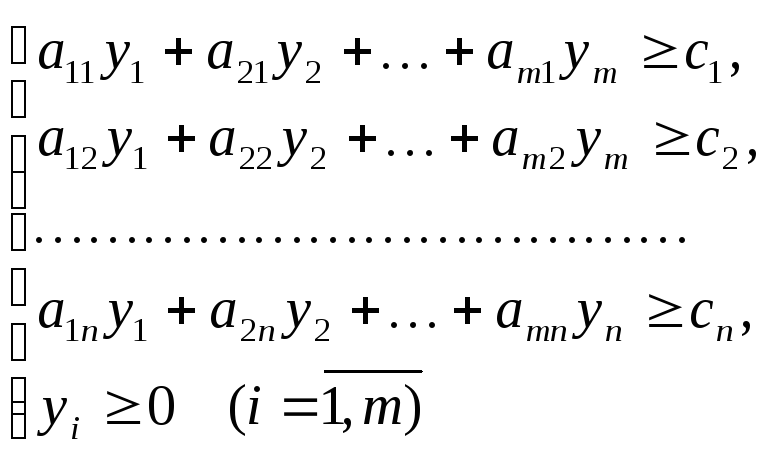
Здесь z — общая оценка ресурсов. Каждое j-е ограничение из системы представляет собой неравенство, левая часть которого равна оценке всех ресурсов, расходуемых на производство единицы j-го вида продукции, а правая — стоимости единицы этой продукции.

Заметим, что ценность видов ресурсов нельзя отождествлять с действительными ценами, по которым осуществляется его закупка. В данном случае речь идет о некоторой мере, имеющей экономическую природу, которая характеризует ценность ресурса только относительно полученного оптимального решения.

Пример

1)

Решение:

Сведем ограничения типа ≥ к ограничениям ≤ умножением на -1.

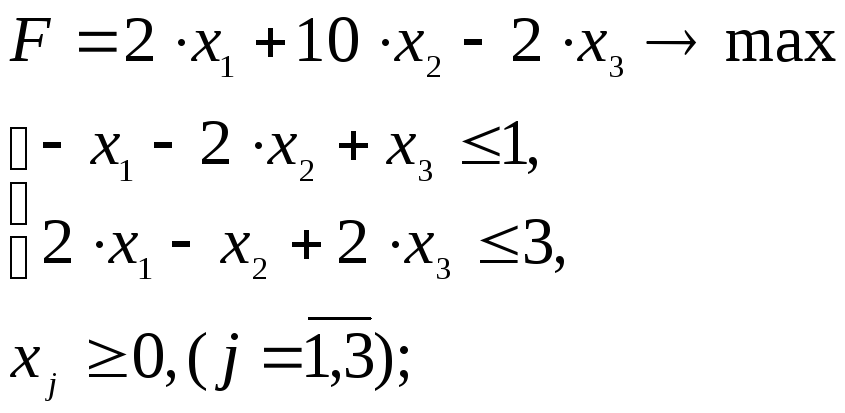
Так на все переменные наложены условия неотрицательности, то в двойственной задаче все ограничения будут являться неравентвами.

Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит три переменные, то двойственная задача будет иметь три ограничения.

Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.

Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.

Учитывая указанные выше правила, имеем двойственную задачу:

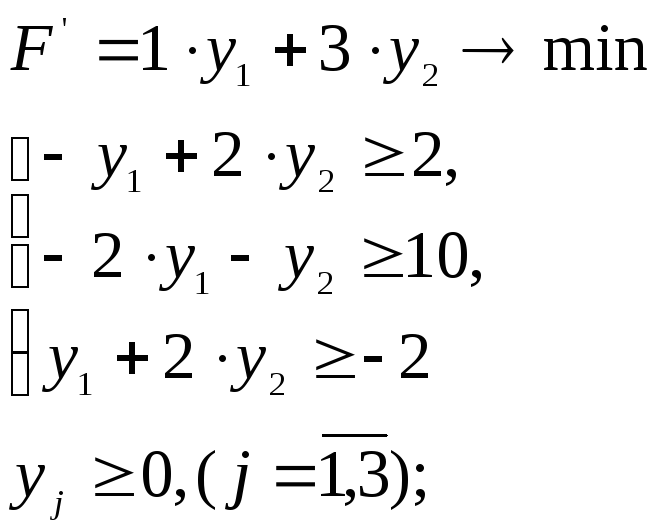
2)

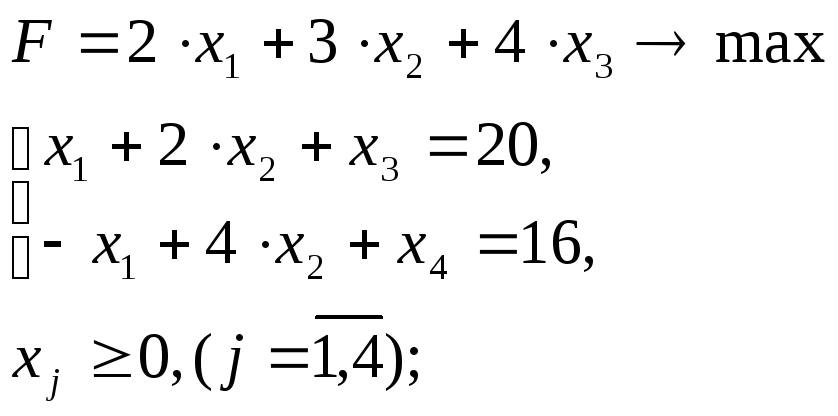
Решение:

Так как на переменные наложены условия неотрицательности, то ограничения двойственной задачи будут ограничениями-неравенствами. Так как ограничения прямой задачи являются равенствами, то на переменные двойственной задачи не накладывается условие неотрицательности.

Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит четыре переменные, то двойственная задача будет иметь четыре ограничения.

Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.

Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.

В результате получим следующую модель двойственной задачи:

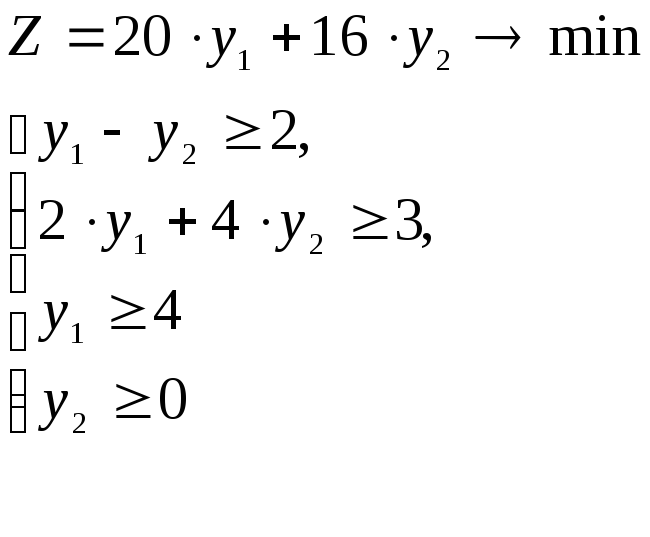
Экономический анализ решения задач линейного программирования

Анализ решения линейной задачи разберем на примере задачи определения оптимального ассортимента выпускаемой продукции.

Пусть задача имеет следующую математическую модель

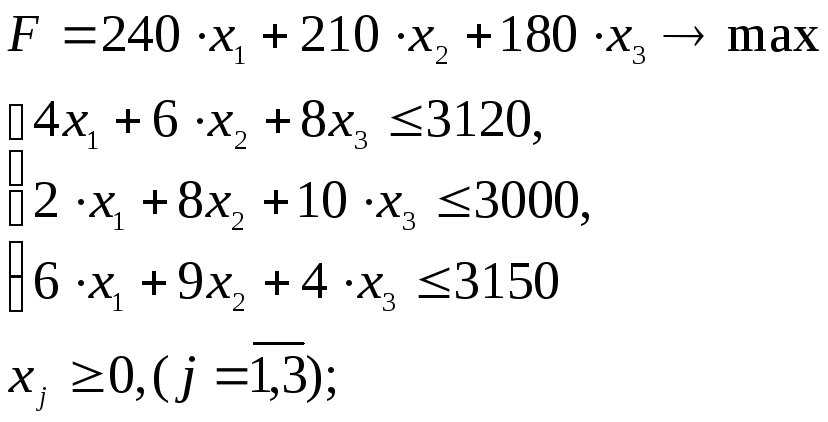
Пусть данные на листе Excel размещены следующим образом

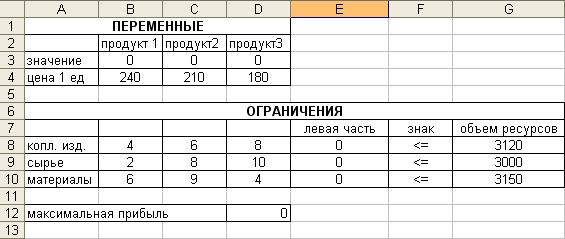
Результат решения:

х1=397,5; х2=0; х3=191,25 Fmax=129 825.

По результатам решения формируется три отчета: по результатам, по устойчивости, по пределам.

Отчет по результатам

Целевая ячейка (Максимум)
	Ячейка	Имя	Исходное значение	Результат
	$D$12	максимальная прибыль	0	129825
Изменяемые ячейки
	Ячейка	Имя	Исходное значение	Результат
	$B$3	значение продукт 1	0	397,5
	$C$3	значение продукт2	0	0
	$D$3	значение продукт3	0	191,25
Ограничения
	Ячейка	Имя	Значение	Формула	Статус	Разница
	$E$8	копл. изд. левая часть	3120	$E$8<=$G$8	связанное	0
	$E$9	сырье левая часть	2707,5	$E$9<=$G$9	не связан.	292,5
	$E$10	материалы левая часть	3150	$E$10<=$G$10	связанное	0

В отчете ПО РЕЗУЛЬТАТАМ приведены значения неизвестных и функции, а также данные о выполнении ограничений. В графе СТАТУС указано, что первое и третье ограничения связанные, а второе - не связанное. Это означает, что первый и третий ресурс используются полностью, а второй (сырье) не использован в объеме 292,5 ед.

Ресурс, который полностью расходится в производстве называется дефицитным, а который находится в излишке – избыточным.

Отчет по устойчивости

Изменяемые ячейки
			Результ.	Нормир.	Целевой	Допустимое	Допустимое
	Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
	$B$3	значение продукт 1	397,5	0	240	30	100
	$C$3	значение продукт2	0	-150	210	150	1,00E+30
	$D$3	значение продукт3	191,25	0	180	300	20
Ограничения
			Результ.	Теневая	Ограничение	Допустимое	Допустимое
	Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
	$E$8	компл. изд. левая часть	3120	3,75	3120	180	1020
	$E$9	сырье левая часть	2707,5	0	3000	1E+30	292,5
	$E$10	материалы левая часть	3150	37,5	3150	1530	390

В отчете по устойчивости а графах ДОПУСТИМОЕ УВЕЛИЧЕНИЕ и ДОПУСТИМОЕ УМЕНЬШЕНИЕ приведены границы устойчивости неизвестных задачи (допустимое увеличение и уменьшение коэффициентов целевой функции), также границы устойчивости теневых цен (двойственных оценок).

Это очень важная информация, так как в модели задачи заложена априорная прибыль от единицы продукции каждого вида. Однако с течением времени могут измениться цены на продукцию или ресурсы, себестоимость продукции в результате влияния различных факторов может оказаться неоптимальным. Поэтому, зная нижние и верхние границы устойчивости критериальных коэффициентов, можно оценить устойчивость решения задачи. Если прибыль каждого вида продукции не выходит за пределы устойчивости, то базис полученного решения остается неизменным. Если же хотя бы одно значение прибыли вышло за границы устойчивости, то это говорит о том, что нужно решить задачу заново при уточненных параметрах прибыли.

Нижняя границы прибыли – это такая прибыль, при достижении которой изделие снимается с производства (если оно выпускалось).

Верхняя граница прибыли – это такая прибыль на данное изделие, что выпуск всех других изделий прекращается и все ресурсы направляются только на выпуск данного изделия.

В графе НОРМИРОВАННАЯ СТОИМОСТЬ элемент второй строки показывает, на сколько уменьшится значение функции, если в решении переменную х₂ увеличить на единицу.

Во втором блоке отчета приведены данные о ресурсах. ТЕНЕВАЯ ЦЕНА (двойственная оценка) показывает дефицитность ресурса и меру его дефицитности.

Третий ресурс (материалы) является самым дефицитным, так как его теневая цена самая высокая. Второй ресурс (сырье) является избыточным, поэтому его теневая цена равна нулю.

Теневая цена показывает, на сколько возрастет (уменьшится) значение функции в оптимальном решении при увеличении ресурса на единицу. Если наличие третьего ресурса будет не 3150, а 3149, то значение целевой функции уменьшится на 37,5. при увеличении ресурса на единицу, значение целевой функции увеличится на единицу.

Таким образом, если наличие ресурса находится в границах устойчивости двойственной оценки, то не решая задачу заново, можно определить величину изменения суммарной прибыли.

Нижняя граница ресурса – это такой объем ресурса, при котором все ресурсы, кроме данного, становятся не дефицитными.

Верхняя граница ресурса – это такой объем ресурса, при котором все ресурсы, кроме данного, становятся дефицитными.

Используя отчет по устойчивости, можно, не решая задачу заново, оценить рентабельность нового продукта. Например, требуется оценить целесообразность введения в план производства четвертого вида продукта, нормы затрат ресурсов которого соответственно равны 5 (комплектность), 6 (сырье) и 6 (материалы) ед., а прибыль от реализации единицы продукта составит 200 ден. ед.

Рассчитаем стоимость ресурсов, расходуемых на единицу этой продукции:

5*3,75 + 6*0 + 6*37,5 = 243,75 ден. ед.

Получаем, что затраты на выпуск продукции превышают прибыль, получаемую за нее. Поэтому выпускать такую продукцию нецелесообразно. Это продукция будет рентабельной при установлении ее цены больше, чем 243,75.

Отчет по пределам

		Целевое
	Ячейка	Имя	Значение
	$D$12	максимальная прибыль	129825
		Изменяемое			Нижний	Целевой		Верхний	Целевой
	Ячейка	Имя	Значение		предел	результат		предел	результат
	$B$3	значение продукт 1	397,5		0	34425		397,5	129825
	$C$3	значение продукт2	0		0	129825		0	129825
	$D$3	значение продукт3	191,25		0	95400		191,25	129825

В отчете по пределам показаны нижние и верхние границы изменения неизвестных и значения целевой функции при этих изменениях. Так, если х₁=0, х2 и х3 оставить без изменений, то F=240*397.5 = 95 400, а при х2=0 и неизменных х1 и х3 f=129 825, т.е. максимальному значению.

Тема: Векторная оптимизация

Дадим математическую формулировку задачи векторной оптимизации.

Пусть Х={x₁,x₂, . . . ,x_N) (j=1…N) – вектор переменных. Обычно предполагается неотрицательность вектора переменных Х>=0. Функциональная взаимосвязь переменных устанавливается определенными отношениями, на которые накладываются ограничения:

g_i(X)<=b_i(i=1…M).

Функционирование системы оценивается определенными критериями, записываемыми в виде целевых функций fk(X) (k=1…K). Множество критериев можно представить в виде векторной целевой функции

F(X) = {f₁(X), … ,f_k(X)}.

Задача многоцелевой оптимизации записывается как векторная задача математического программирования:

F(X) = {f₁(X), … , f_k(X)}.

g_i(X)<=b_i (i=1…M). (1)

Х>=0.

Будем рассматривать случай, когда точки оптимума X_k^*(k=1…K), полученные при решении задачи по каждому критериюf_k(k=1…K) не совпадают. Поэтому с математической точки зрения задача (1) является некорректной, так как если один из критериев достигает своего оптимума, то улучшение по другим компонентам векторного критерия невозможно. Отсюда вытекает вывод, что решением векторной задачи может быть только некоторое компромиссное решение.

Особенностью задач векторной оптимизации является наличие в области допустимых значений области компромиссов, в которой невозможно одновременное улучшение всех критериев. Принадлежащие области компромиссов планы называются эффективными или оптимальными по Парето.

Введем понятие предпочтительного плана. План Х0 не хуже плана Х’, если f_k(X₀)>=f_k(X’) (k=1…K). Если среди этих неравенств хотя бы одно строгое, то план Х₀предпочтительнее (лучше)X’, т. е. при переходе от Х0 к Х’ значение ни одного критерия не ухудшилось и хотя бы одного критерия улучшилось. План Х₀оптимален по Парето (эффективен), если он допустим и не существует другого плана Х’, для которогоf_k(X₀)>=f_k(X’) (k=1…K), и хотя бы для одного критерия выполняется строгое равенство.

При разработке методов решения векторных задач приходится решать ряд специфических проблем.

Проблема нормализациивозникает в связи с тем, что локальные критерии имеют, как правило, различные единицы и масштабы измерения, и это делает невозможным их непосредственное сравнение. Операция приведения критериев к единому масштабу и безразмерному виду носит названиенормализации. Наиболее распространенным способом нормирования является замена абсолютных значений критериев их безразмерными относительными величинами

или относительными значениями отклонений от оптимальных значений критериев

Метод линейной комбинации частных критериев

Пусть задан вектор весовых коэффициентов критериев a= {a1,a2, …,ak}, характеризующих важность соответствующего критерия,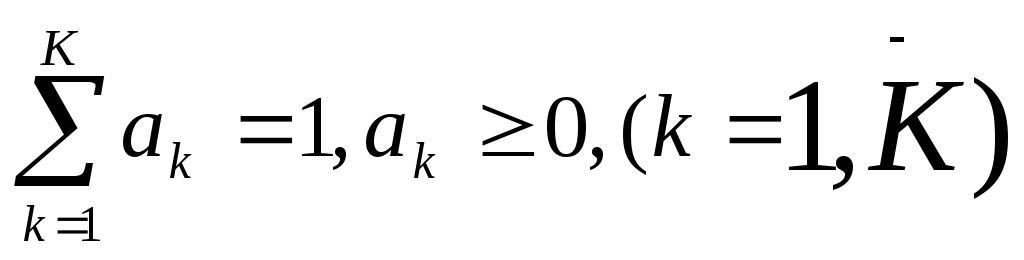. Линейная скаляризованная функция представляет собой сумму частных критериев, умноженных на весовые коэффициенты. Задача становится однокритериальной и имеет вид

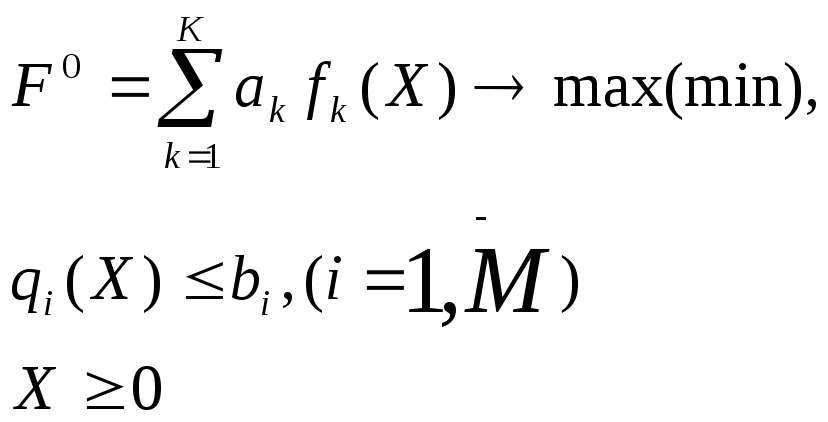
Критерии в свертке могут быть нормированы.

Метод ведущего критерия

Все целевые функции кроме одной переводятся в разряд ограничений. Пусть - вектор, компоненты которого представляют собой нижние границы соответствующих критериев. Задача будет иметь вид:

Метод последовательных уступок

1. Критерии нумеруются в порядке убывания важности.

2. Определяется значение . Лицом, принимающим решение, устанавливается величина уступки по этому критерию.

3. Решается задача по критерию с дополнительным ограничением

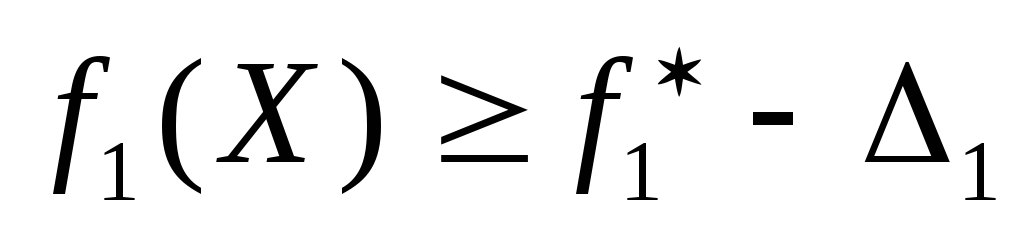
Далее пункты 2 и 3 повторяются для критерия, ... , . Полученное решение не всегда принадлежит области компромиссов.

Пример

Решить задачу

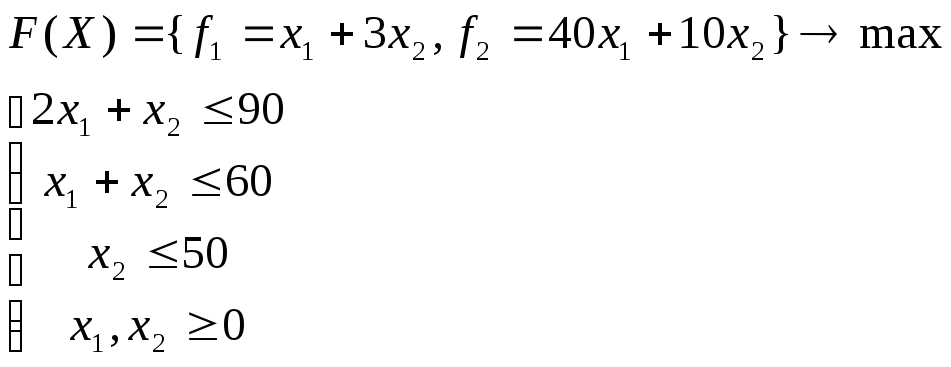
методом последовательных уступок, если уступка по первому критерию составляет 10% от его оптимального значения.

Решение

1. Решаем задачу по критерию f₁. Получимf₁^*=160.

2. В соответствии с условием задачи величина уступки равна ₁=16. Дополнительное ограничение будет иметь вид 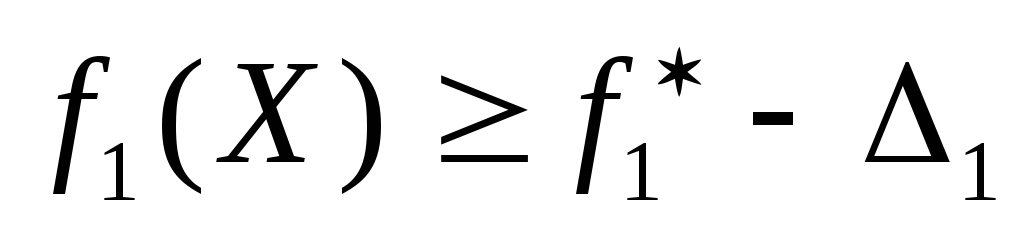, то есть 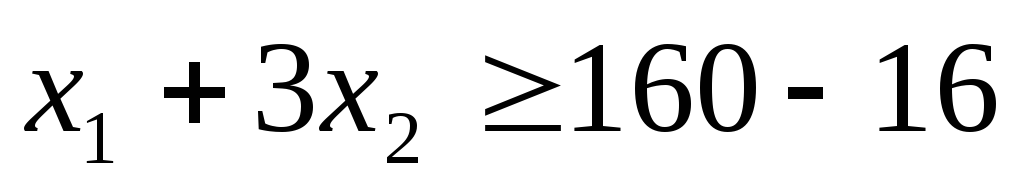. Решая задачу

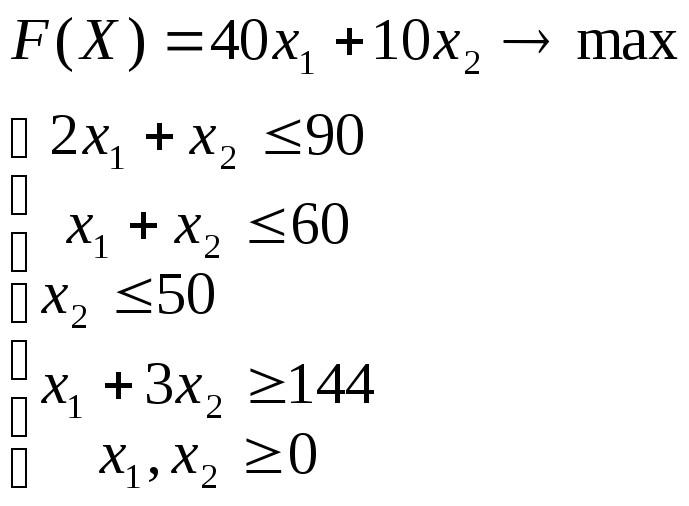
получим Х^*=(18, 42),f₁(X^*)= 144,f₂(X^*)= 1440.

Метод равных наименьших относительных отклонений

Относительное отклонение критерия f_k, будет иметь вид

Целевая функция будет иметь вид

,

а условие равенства отклонений добавит к системе ограничений К-1 равенство вида

Решение может быть неэффективным, потому предварительно необходимо выделить область компромиссов.

Пример

Решить задачу

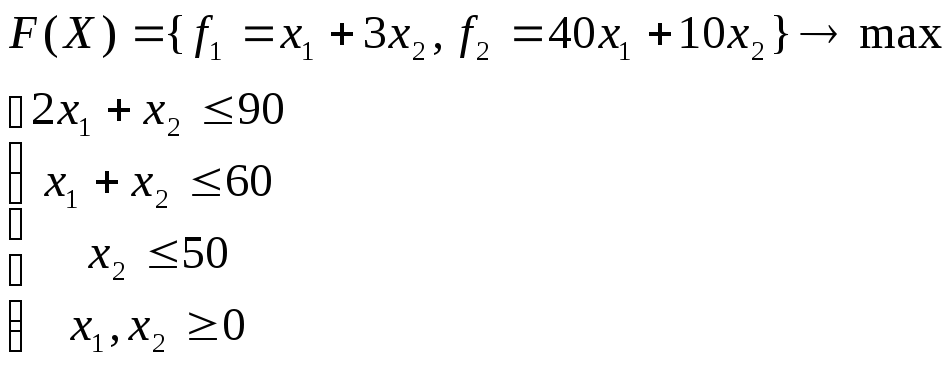
методом равных наименьших отклонений.

Решение

1. Решаем только по первому критерию. Находим f₁^*=160.

2. Решаем только по второму критерию. Находим f₂^*=1800.

3. Находим относительные отклонения для каждого критерия:

Поскольку оба критерия максимизируются, знак модуля можно опустить. Приравнивая величины отклонений , получаем дополнительное ограничение

23х₁= 19х₂.

В итоге задача примет вид

В результате решения Х^*=(27, 3; 32, 9),f₁(X^*)= 125,8,f₂(X^*)= 1413.