4. Правило Крамера для системи n лінійних рівнянь з n невідомими

Подібно до того, як, використовуючи визначники другого і третього порядків, розв’язують квадратні лінійні системи з двома і трьома невідомими, за допомогою визначників n-го порядку можна розв’язувати квадратні системи лінійних рівнянь з n невідомими.

Розглянемо систему n лінійних рівнянь з n невідомими

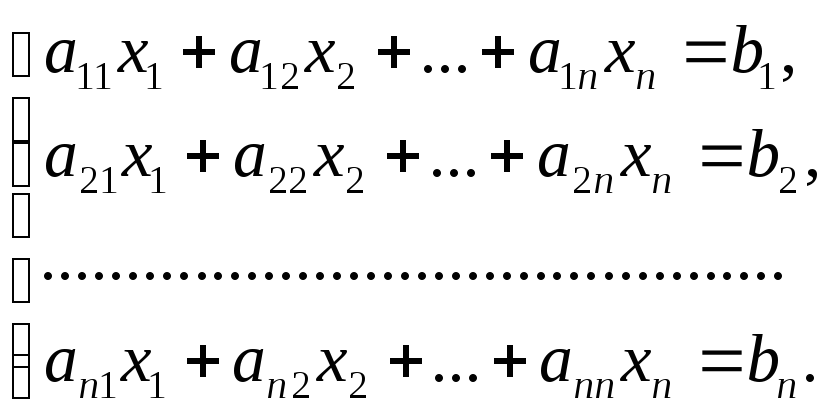
(10)

Запишемо систему (10) у матрично-векторній формі

– матриця системи. Вважатимемо, що визначник Δ матриці системи (10) відмінний від нуля (Δ≠0).

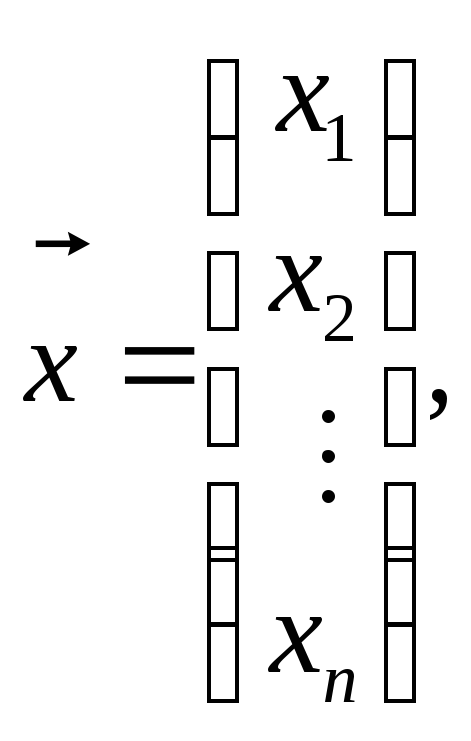
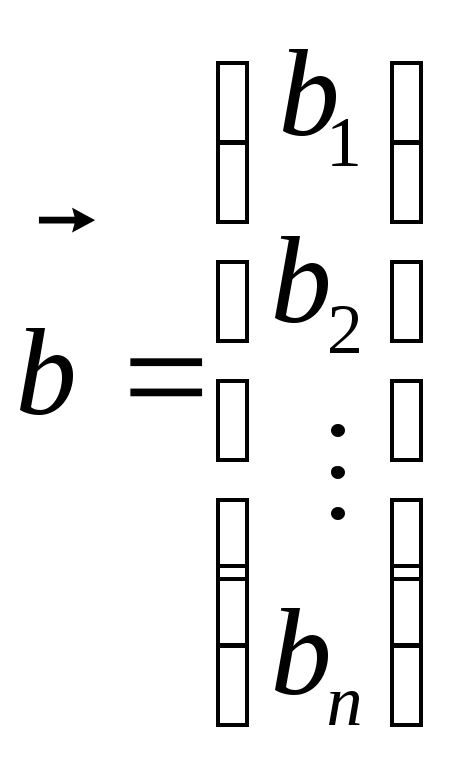
– одно стовпцеві матриці. Оскільки А – квадратна, невироджена матриця, то для неї існує обернена А^-1. Тому розв’язок системи (10) можна подати у вигляді

Або

=

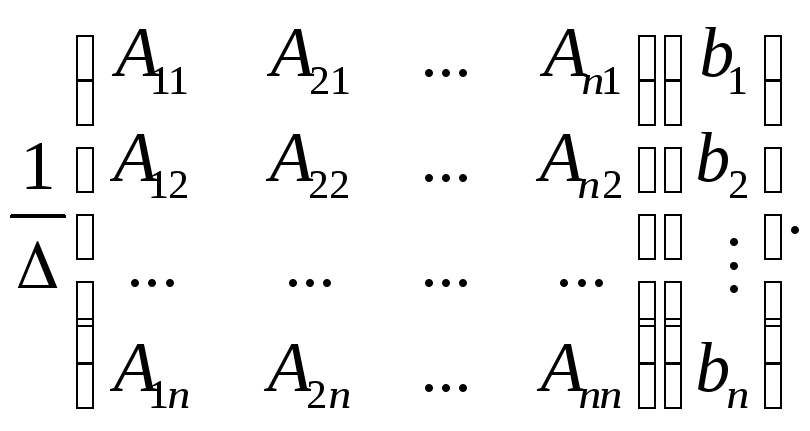
Перемноживши матриці в правій частині, дістанемо

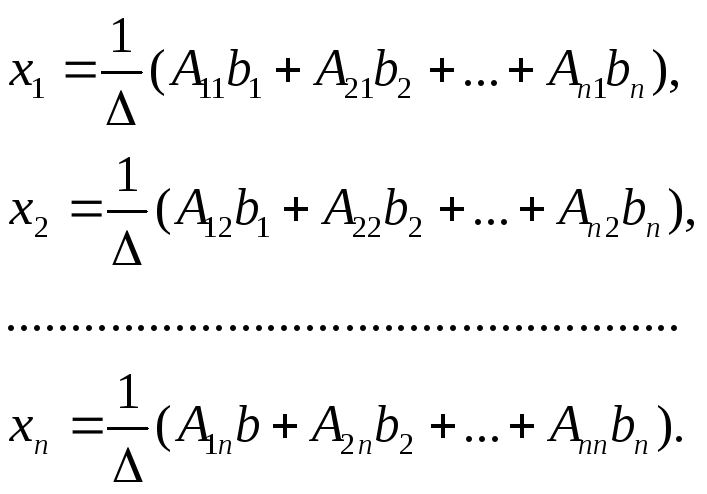
–розклад за першим стовпцем визначника

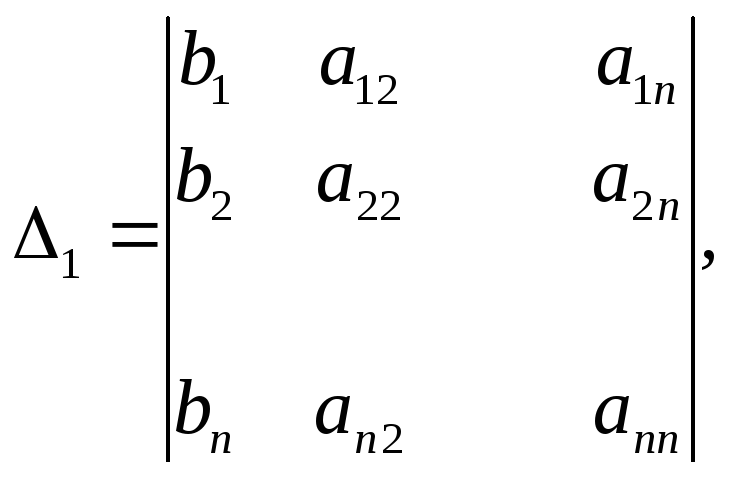
Який дістаємо з визначника Δ заміною першого його стовпця стовпцем вільних членів системи. Отже,

Аналогічно, де - визначник, який дістаємо з визначника заміною

другого його стовпця стовпцем вільних членів і т.д., ().

Таким чином, довели таке твердження.

Теорема 5. Якщо визначник Δ системи n-лінійних рівнянь з n невідомими відмінний від нуля, то система має єдиний розв’язок:

…, (11)

де () – визначник, який дістаємо з визначника Δ заміною йогоi-го стовпця стовпцем вільних членів системи.

Формули (11) називають формулами Крамера, а теорему 5 – правилом Крамера.

Якщо Δ=0, а , то в цьому випадку система несумісна (ранг основної матриці ≠ рангу розширеної).

Однорідна система n лінійних рівнянь з n невідомими має єдиний розв’язок, якщо Δ≠0; якщо Δ=0, то вона має ненульові розв’язки.

Зауважимо, що розв’язування систем лінійних рівнянь за правилом Крамера пов’язане з досить громісткими обчисленнями: для розв’язування квадратної системи з n невідомими слід обчислити n+1 визначників n-го порядку. З практичної точки зору більш зручним є метод Гаусса.

Приклад. Розв’язати систему лінійних рівнянь

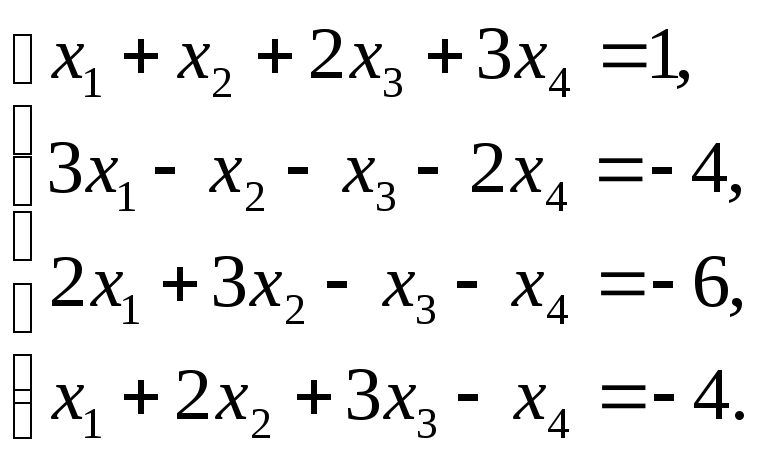
Розв’язання. Визначник цієї системи відмінний від нуля,

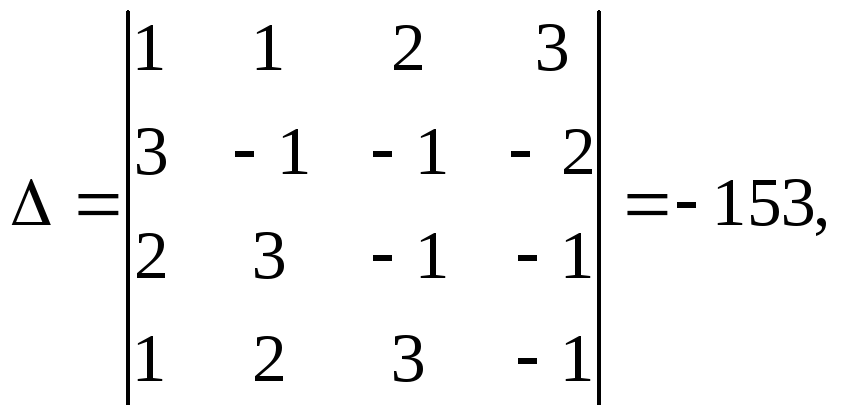
тому систему розв’яжемо за правилом Крамера:

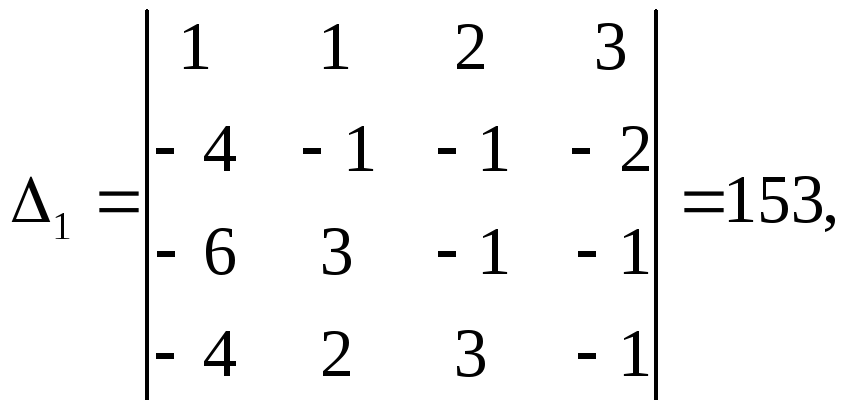
Отже, розв’язком заданої системи є

Вправи для самостійного розв’язування

1. Довести тотожність:

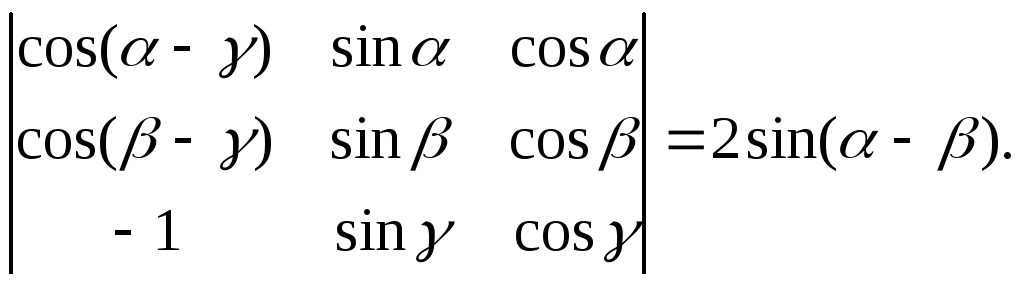
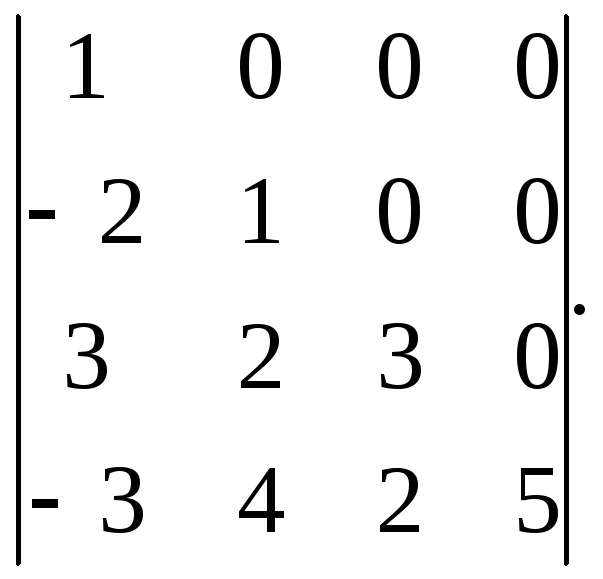
2. Обчислити добуток визначників:

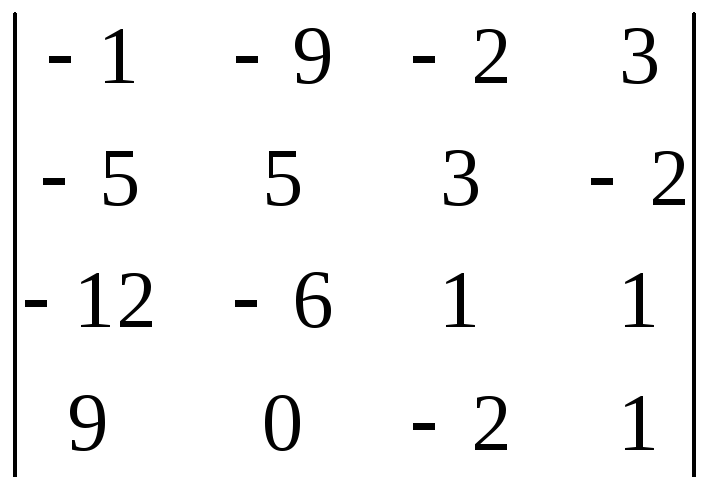
3. Обчислити ранг матриці методом окантування мінорів:

а) б)

4. Обчислити матрицю, обернену до даної матриці за допомогою алгебраїчних доповнень:

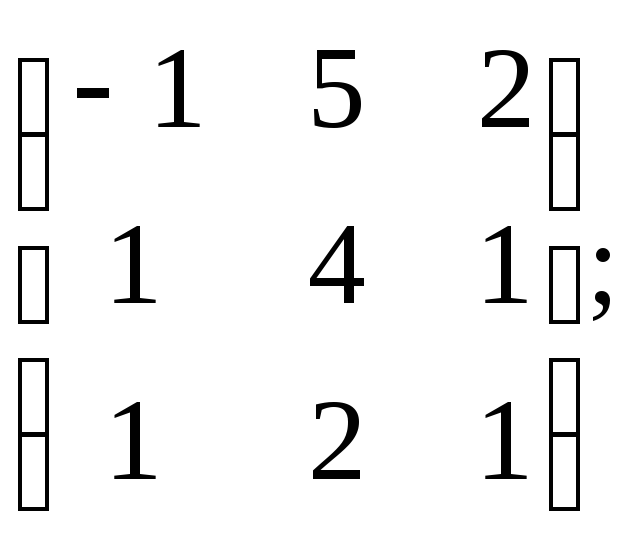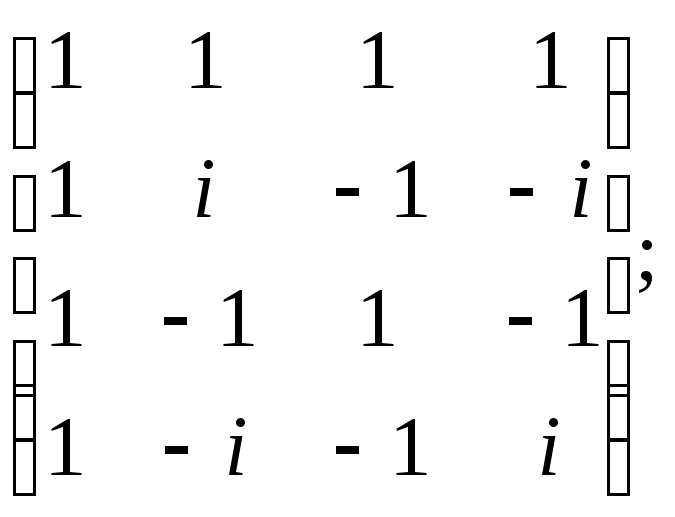а) б)в)

5. Розв’язати матричне рівняння:

а) б)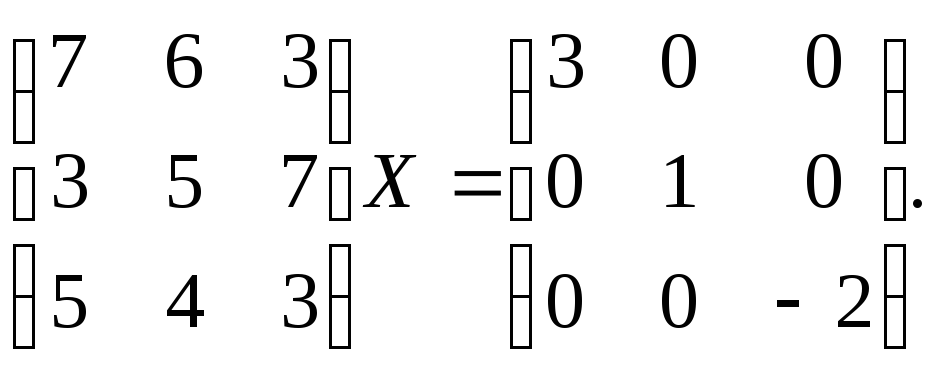

6. Розв’язати систему рівнянь за формулами Крамера:

а) 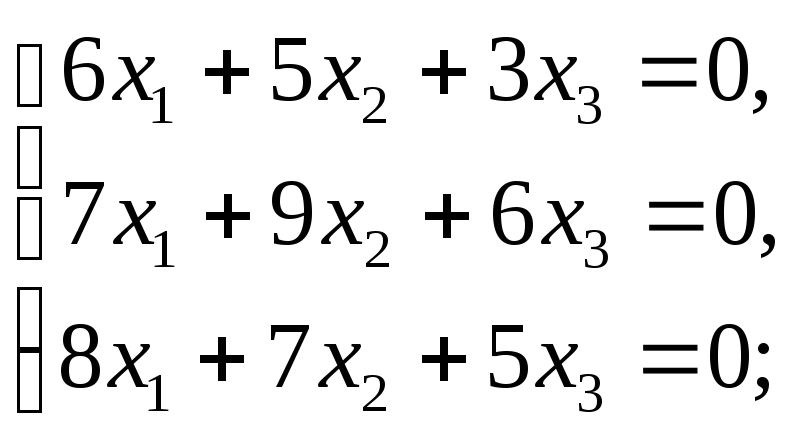б)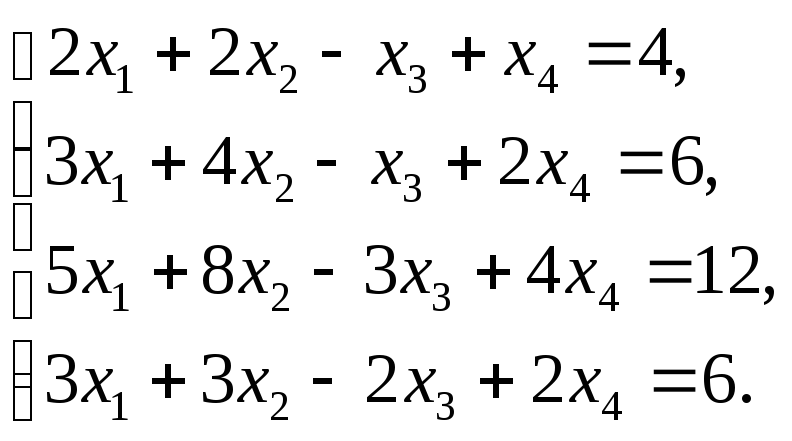

Література

1. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теорія чисел . – К.: Вища школа, 1977. – ч.1.

2. Костарчук В.М., Хацет Б.І. Курс вищої алгебри. – К.: Вища школа, 1969.

3. Завало С.Т. Курс алгебри. – К.: Вища школа, 1985.

4. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1969.

5. Окунев Л.Я. Высшая алгебра. – М.: Просвещение, 1966.

6. Варпаховский Ф.Л., Солодовников А.С., Стеллецкий И.В. Алгебра. – М.: Просвещение, 1978.

7. Вівальнюк Л.М. Алгебра і теорія чисел. Поля. Системи лінійних рівнянь. – К.: Вища школа, 1972.

8. Костыркин А.И. Введение в алгебру. – М.: Наука, 1977.

9. Куликов Л.Я. Алгебра и теория чисел. – М.: Высшая школа, 1979.

10. Ляпин Е.С., Евсеев А.Е. Алгебра и теорія чисел: в 2-х ч. – М.: Просвещение, 1974.

11. Скорняков Л.А. Элементи алгебры. – М.: Наука, 1980.

12. Головина Л.И. Линейная алгебра и некоторые её приложения. – 3-е узд. – М.: Наука, 1979.

13. Воеводин В.В. Линейная алгебра. – М.: Наука, 1974.

14. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967.

15. Ленг С. Алгебра. – М.: Мир, 1968.

16. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976.

17. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1972.

18. Завало С.Т. та ін. Алгебра і теорія чисел. Практикум. – К.: Вища школа, 1983.

19. Шнеперман Л.Б. Сборник задач по алгебре и теории чисел. – Минск: Вышэйш. Шк., 1982.