Вправи для самостійного розв’язування

1. Розв’язати системи за правилом Крамера

а) б)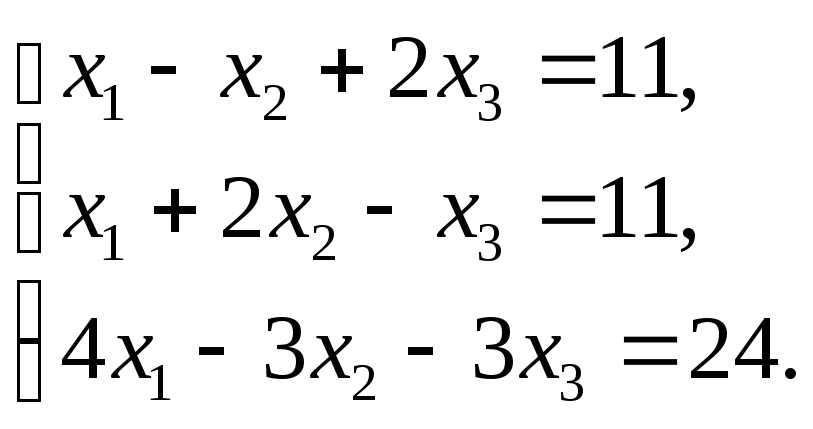

2. Знайти число інверсій в перестановках:

а) (5, 4, 1, 7, 6, 3, 2); б) (n, n-1, … , 2, 1); в) (7, 6, 9, 1, 2, 3, 5, 8, 4).

3. Чи парні підстановки?

а) б)

3. Обчислити всі мінори другого порядку визначника

3. Обчислити алгебраїчні доповнення елементів 3-го стовпця визначника

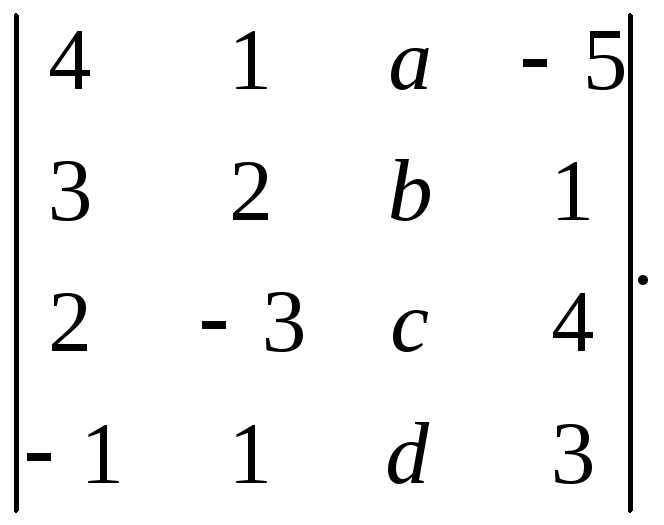
3. Обчислити коефіцієнт числа x у визначнику

3. Обчислити визначники

а) 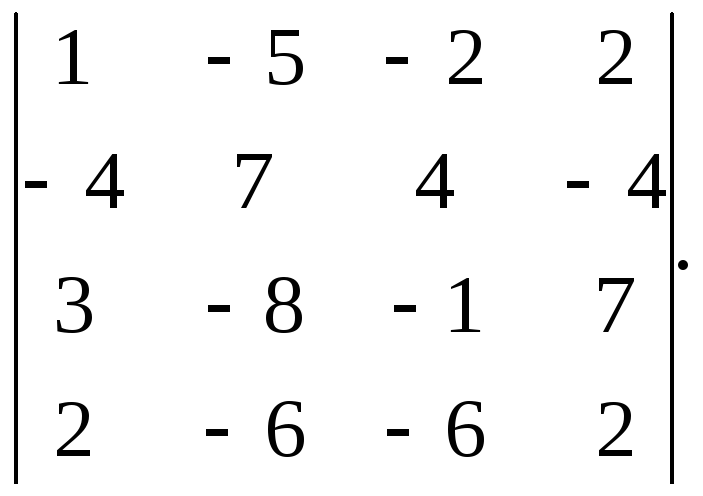б)

8. Розв’язати рівняння:

а) 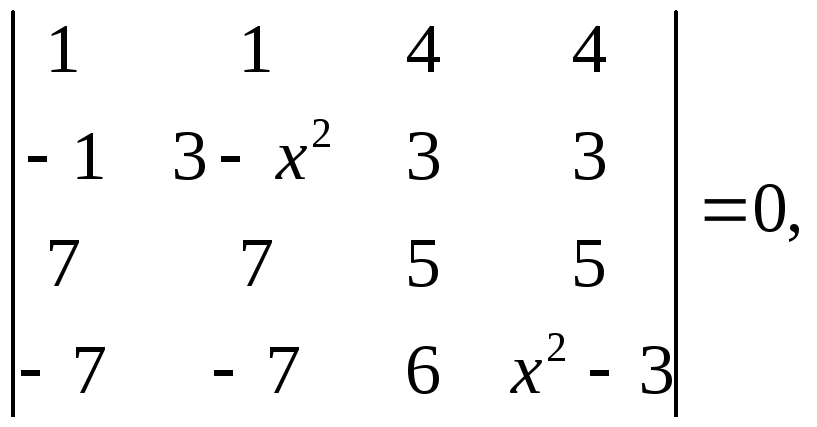б)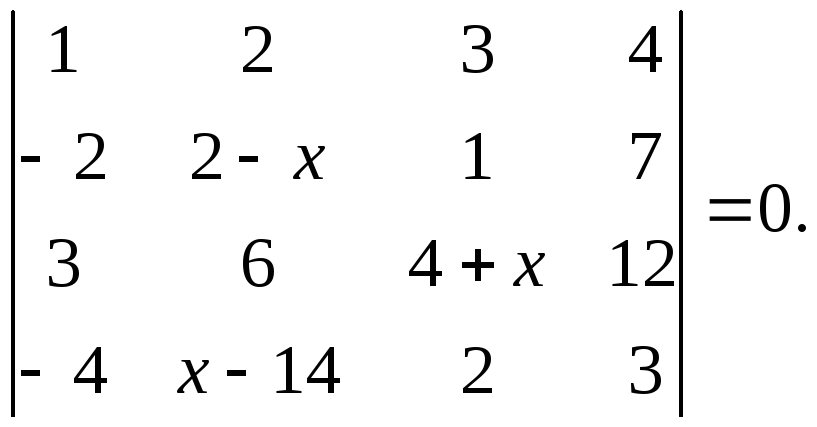

§ 7. Застосування визначників

1. Визначник добутку матриць

Важливу роль у теорії матриць відіграє таке твердження .

Теорема 1. Визначник добутку двох квадратних матриць n-го порядку дорівнює добутку визначників цих матриць.

► Нехай А і В – довільно вибрані матриці n-го порядку. Треба довести, що виконується рівність

(1)

Формула (1) правильна, якщо одна з матриць одинична. Дійсно , AE=A, тому Отже,

Лема. Якщо справедлива рівність

(2)

то справедлива і рівність

(3)

де матриця отримана з одним з рядкових перетворень.

Доведемо лему. Нехай матрицю дістаємо із матриці одним із перетворень:

1. переставлення рядків;

2. множення будь-якого рядка матриці на число k, відмінне від нуля;

3. додавання до одного рядка матриці іншого її рядка, помноженого на деяке число, відмінне від нуля.

Матрицю дістаємо з таким же перетворенням.

У випадку 1) матрицю отримуємо з переставленням рядків. Тому

(4)

(при переставленні рядків визначник помножається на –1).

У випадку 2) маємо

(5)

У випадку перетворення 3) дістаємо відповідно

(6)

Враховуючи (2) і (4), приходимо до рівності

Із (2) і (5) маємо

А із (2) і (6) відповідно отримуємо

Таким чином, будь-яка пара рівностей (4), (5) чи (6) в поєднанні з (2) дає (3). Лему доведено.

Із щойно доведеної леми та із рівності випливає справедливість формули (1), оскільки матрицюB можна дістати із E при допомозі перетворень 1), 2), 3). Матриця B не вироджена. Якщо ж матриця B вироджена, тобто якщо її рядки лінійно залежні, то така ж залежність існує і між рядками AB (§4, п.3, Лема 1). Отже, матриця AB також вироджена.

Таким чином, маємо і ◄

Наслідок. Для того, щоб квадратна матриця мала обернену, необхідно, щоб її визначник був відмінний від нуля.

► Нехай існує матриця А^-1 така, що АА^-1=Е. Тоді за теоремою 1 маємо ◄

Отже, можна дати ще таке означення не виродженої матриці: квадратна матриця А називається не виродженою (неособливою), якщо її визначник відмінний від нуля.

Доведену теорему 1 можна поширити методом індукції на будь-яке скінченне число множників.

2. Означення рангу матриці через мінори. Теорема про ранг матриці. Умова виродженості квадратної матриці

Розглянемо ще один спосіб обчислення рангу матриці, за допомогою якого можна не лише обчислити ранг матриці, а й знайти лінійно незалежні підсистеми системи рядків і системи стовпців матриці. Нехай

довільна матриця розміру з елементами із поля P.

Виберемо в матриці А довільно k рядків і k стовпців (k). Елементи матриці А, що стоять на перетині вибраних рядків і стовпців, утворюють квадратну матрицю порядку k. Визначник цієї матриці називається мінором k-го порядку матриці. Мінори (n-1)-го порядку є окремим випадком мінорів k-го порядку при k= n-1. Елементи матриці А можна вважати мінорами першого порядку.

Якщо матриця А відмінна від нульової, то серед її мінорів є відмінні від нуля.

Для будь-якої матриці А справедливе таке твердження:

Якщо всі мінори k-го порядку матриці А дорівнюють нулю, то дорівнюють нулю і всі її мінори більш високих порядків.

Справді, розклавши всякий мінор порядку k+1 за елементами першого рядка, запишемо його у вигляді суми мінорів k-го порядку, помножених на деякі числа. Оскільки всі мінори k-го порядку дорівнюють нулю, то й розкладений мінор порядку k+1 також дорівнює нулю. Аналогічно доведемо, що дорівнюють нулю всі мінори порядку k+2, порядку k+3 і т.д.

Теорема 2. Для того, щоб визначник квадратної матриці А n-го порядку дорівнював нулю, необхідно і достатньо, щоб ранг цієї матриці був менший її порядку.

► Нехай А=() – матриця розміру . Треба довести, що

Достатність. Якщо , то система векторів-рядків матриці А лінійно залежна. Це означає, що хоч один з них є лінійною комбінацією інших. В силу властивості 8 визначника, отримуємо:

Необхідність. Нехай Доведемо,що , тобто що система векторів-рядків матриці А лінійно залежна. Припустимо, що ця система лінійно незалежна. Тоді виконується рівність

при умові, що

Розглянемо однорідну систему, розв’язками якої є числа

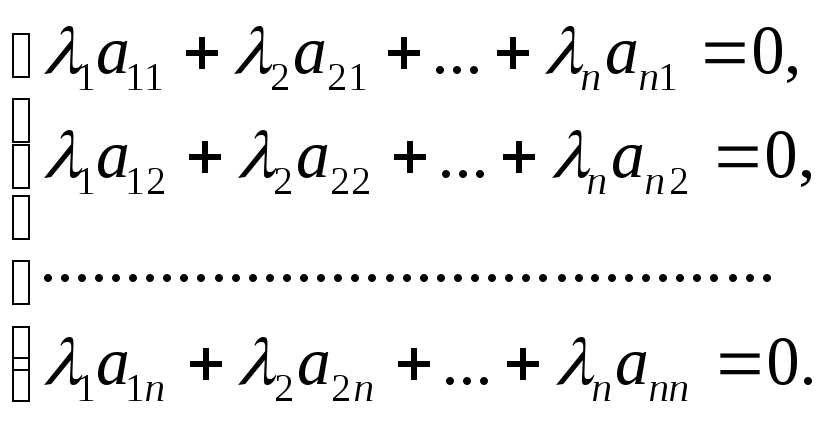
Ця система має нульовий розв’язок, тому її визначник відмінний від нуля

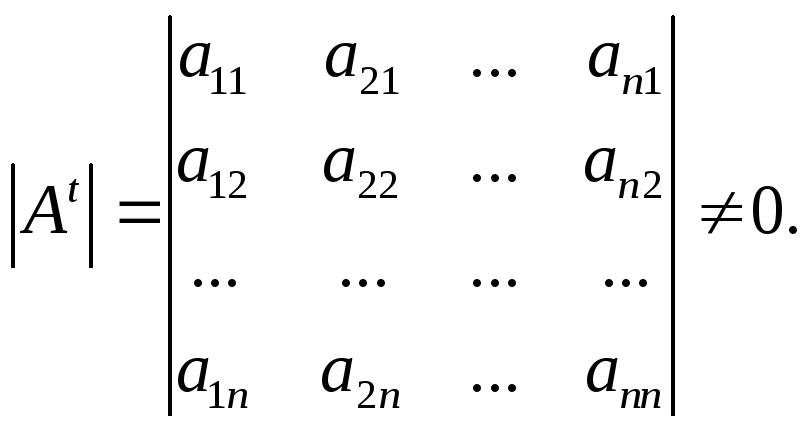
Оскільки визначник матриці не змінюється при її транспонуванні, то отримуємо:

Отже, а це суперечить припущенню. Припустивши, що система векторів-рядків лінійно незалежна, ми прийшли до протиріччя.◄

Наслідок 1. Визначник дорівнює нулю тоді і тільки тоді, коли його рядки (стовпці) утворюють лінійно залежну систему векторів.

Дійсно, лінійна залежність рівносильна тому, що ранг системи її векторів, а, отже, і ранг матриці, менше її порядку.

Наслідок 2. Квадратна матриця є особливою тоді і тільки тоді, коли її визначник дорівнює нулю.

Це випливає із означення особливої матриці: квадратна матриця А n-го порядку особлива, якщо .

Наслідок 3. Добуток двох неособливих матриць – неособлива матриця. Добуток двох матриць, з яких хоч одна особлива – особлива матриця.

Це випливає з теореми про визначник добутку двох матриць.

Теорема 3. (про ранг матриці).

Для того, щоб ранг матриці дорівнював r, необхідно і достатньо, щоб серед мінорів матриці знайшовся хоч один мінор r-го порядку, відмінний від нуля, а всі мінори (r+1)-го порядку були б рівні нулю.

► Необхідність. Нехай А – довільна матриця, ранг якої дорівнює r. Покажемо, що існує мінор r-го порядку матриці А, відмінний від нуля. Оскільки ранг матриці дорівнює r, то існує базис системи векторів-рядків, що складається із r рядків. Можна вважати, що перші r рядків утворюють цей базис.

Розглянемо матрицю

Її рядковий ранг дорівнює r, стовпцевий ранг також дорівнює r. Тому існує базис системи векторів-стовпців матриці із r стовпців. Нехай цим базисом є підсистема перших r стовпців. Розглянемо визначник

(7)

Система його стовпців (рядків) (укорочених векторів-рядків матриці А) є лінійно незалежною. За наслідком 1 теореми 2, Отже, знайшовся мінор r-го порядку матриці А, відмінний від нуля.

Мінори r+1 порядку матриці А всі дорівнюють нулю. Дійсно, за умовою, будь-яка система із r+1 рядків матриці А лінійно залежна. Тому лінійно залежна і система із r+1 укорочених векторів-рядків. Отже, рядки будь-якого мінора (r+1)-го порядку утворюють лінійно залежну систему, тому цей мінор дорівнює нулю.

Достатність. Нехай серед мінорів матриці А існує мінор r-го порядку , а всі мінори (r+1)-го порядку дорівнюють нулю. Можна вважати, що мінор розміщений у верхньому лівому куту матриці А, тобто має вигляд (7). Рядки і стовпці визначника утворюють лінійно незалежну систему векторів. Звідси випливає, що в матриці А перші r рядків утворюють лінійно незалежну систему: якби ця система була лінійно залежною, то такою була б і система укорочених векторів-рядків визначника, що протирічить умові. Таким чином, ранг матриці А не менший r. Якщо припустити, що , то це означало б, що існує мінор -го порядку, відмінний від нуля. А це протирічить тому, що всі мінори (r+1)-го порядку (отже, і порядку ) дорівнюють нулю.

Таким чином, . ◄

З теореми 3 випливає наступне означення рангу матриці.

Означення 1. Рангом матриці А називається найвищий порядок її мінорів відмінних від нуля.