Рівняння Пфаффа

Нехай в області D с R³ задано диференціальну форму

ω := а(х)dх := а₁(x) dx₁ + ... + а_n(x) dx_n

з неперервно диференційовними коефіцієнтами а_і : D → R , i =1, …, n. Усюди надалі ми розглядатимемо лише невироджений випадок, для якого виконується умова || а(х) || ≠ 0 х є D.

Рівняння вигляду

ω = 0 (1)

називається рівнянням Пфаффа.

При n = 2 це рівняння знайоме нам. Тепер ми зробимо це в загальному випадку. Ставлячи кожній точці х₀ D у відповідність гіперплощину

Р(х₀) : а₁(х₀)(х₁ - х₀₁) + ... + а_n(х₀) (х_n – х_0n) = 0, (2)

ортогональну до вектора а_n(х₀), рівняння (1) задає в області D поле гіперплощин Р. Природно сформулювати задачу про відшукання k-ви­мірної (k ≤ n - 1) інтегральної поверхні поля Р, тобто такої поверхні, яка в кожній своїй точці х₀ дотикається відповідної гіперплощини Р(х₀). Про таку поверхню можна також сказати, що вона ортогональна до векторного поля а(х). Для k -вимірної поверхні, заданої параметрични­ми рівняннями

х = х(s), х(s) С¹ (D → D),

де D — область у R^k, умова інтегральності виражається тотожністю

a(x(s))dx(s) ≡ 0.

Основою для рівняння Пфаффа є задача відшукання інтегральних поверхонь максимально можливої вимірності k = n – 1.

Виникає завдання про знаходження сімейства поверхонь U (x, y, z) = c, ортогональних до векторних лініq. Рівняння таких поверхонь має вигляд (F• t) = 0. Де t - віктор, що лежить в дотичній площині до шуканих поверхонь:

t = i dx + j dy + k dz,

aбо в розгорнутому вигляді

Р (х, у, z) dx + Q (x, у, z) dy + R (x, у, z) dz = 0. (3)

Рівняння вигляду (3) називаються рівняннями Пфаффа.

Якщо поле F = Pi+Qj+Rk потенційне:

F = grad U, тобто

то шуканими поверхнями є поверхні рівня U (x, y, z) = c з потенційною функції U. В цьому випадку знаходження шуканих поверхонь не становить труднощів, оскільки

де криволінійний інтеграл береться на будь-якому шляху між обраною фіксованою точкою (x₀, y₀, z₀) і точкою зі змінними координатами (х, у, z), наприклад, по ламаній, що складається з прямолінійних відрізків, паралельних осям координат.

Якщо ж поле F не потенційне, то в деяких випадках можна підібрати скалярний множник µ(х, у, z), після множення на який вектора F поле стає потенційним.

Якщо такий множник існує, то µ F = grad U або

і, отже,

або

Примножуючи перше з цих тотожностей на R, друге на P, третє на Q і складаючи почленно всі три тотожності, отримаємо необхідну умову існування інтегруючого множника µ:

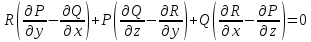
або (F• rot F) = 0, де вектор rol F - вихор поля - визначається рівністю

Якщо ця умова, яка називається умовою повної інтегровності рівняння (3), не виконується, то не існує сімейства поверхностей U (x, y, z) = c, ортогональних векторним лініям поля F (x, у, z).

Дійсно, якщо б таке сімейство U (x, y, z) = c існувало, то ліва частина рівняння (3) могла б відрізнятися від

лише деяким множником µ(x, у, z), який і був би інтегровним множником рівняння (3).

Отже, для існування сімейства поверхонь U (x, y, z) = c, ортогональних векторним лініям векторного поля F, необхідно, щоб вектори F і rot F були б ортогональні, тобто (F• rot F) = 0.

Зауваження. Умова (F• rot F) = 0 називається також умовою інтегровності рівняння Пфаффа Р dx + Q dy + R dz = 0 одним співвідношенням U (x, y, z) = c.

Іноді потрібно визначити не поверхні, ортогональні векторним лініям поля F, а лінії, що володіють тією ж властивістю, іншими словами, треба проінтегрувати рівняння Пфаффа не одним, а двома співвідношеннями:

U₁ (x, y, z) = 0 та U₂ (x, y, z) = 0. (4)

Для знаходження таких ліній можна одне з рівнянь (4) задати довільно, наприклад

U₁ (x, y, z) = 0, (5)

і, виключивши з рівняння (3) за допомогою рівняння (5) одну з змінних, наприклад z, отримаємо диференціальне рівнянняння виду

М (х, y) dx + N (x, y) dy = 0,

інтегруючи яке, знайдемо шукані лінії на довільно обраній поверхні U₁ (x, y, z) = 0.

Покажемо, що умова (F • rot F) = 0 є не тільки необхідним, але і достатнім для існування сімейства поверхностей, ортогональних векторним лініям.

Зауважимо, що на шуканих поверхнях U (x, y, z) = c повинно обертатися в тотожність рівняння

Р dx + Q dy + R dz = 0

або, що те ж саме, на цих поверхнях криволінійний інтеграл

(6)

має дорівнювати нулю по будь-якому шляху (в тому числі і по незамкнутим шляхам).

Розглянемо всілякі вихрові поверхні, тобто векторні поверхні поля rot F. Очевидно, що в силу теореми Стокса

де dr = i dx + j dy + k dz, і інтеграл (6) по будь-якому замкнутому шляху на вихровий поверхні дорівнює нулю (так як скалярний добуток одиничного вектора нормалі до поверхні n і вектора rot F дорівнює нулю). Виберемо тепер серед вихрових поверхонь ті, на яких всі інтеграли

по незамкнутим шляхах також равні нулю. Для побудови такої поверхні, що проходить через задану точку М (x₀, y₀, z₀), проведемо через цю точку М якусь лінію, ортогональну векторним лініям поля F. Такі лінії визначаються рівнянням

Р dx + Q dy + R dz = 0 , (3)

до якого додано рівняння довільної поверхні z=f (x, у), що проходить через точку М (найчастіше рівняння цієї поповерхні беруть у вигляді z = f₁ (x) або z = f₂ (y) або навіть у вигляді z = a, де а - константа). Підставляючи z = f (x, у) в (3), отримаємо звичайне рівняння виду

М (х, y) dx + N (x, y) dy = 0,

інтегруючи яке і враховуючи початкову умову у (х₀) = у₀, отримаємо шукану криву l, що проходить через точку М (x₀, y₀, z₀) і ортогональну векторним лініям (рис. 1).

Якщо ця лінія не є лінією вихору, то, проводячи через кажну точку лінії l лінію вихору, отримаємо шукану поверхню S, ортогональну векторним лініям поля F.

Дійсно, взявши будь-яку незамкнену криву l на поверхні S (рис. 1) і провівши через її граничні точки вихрові лінії до перетину з кривою l в точках р₁ і р₂, отримаємо замкнутий контур, що складається з відрізка лінії l між точками р₁ і р₂, кривої l і двох вихрових ліній.

Криволінійний інтеграл . Взятий з цьогозамкнутого контуру С, дорівнює нулю, так як контур лежить на вихровій поверхні, причому той же інтеграл, узятий на відрізку дуги l, і по відрізках вихрових ліній дорівнює нулю, так як дуга l і вихрові лінії ортогональні векторним лініях поля F (вихрові лінії ортогональні векторним лініях поля F в силу умови (F • rot F) = 0). Отже, інтеграл подовільно обраному нами незамкнутому шляху l дорівнює нулю, тобто поверхня S є інтегральною поверхнею рівняння (3), що проходить через задану точку М.

Цей метод доказу достатності умови (F • rot F) = 0 для існування сімейства поверхонь, ортогональних векторним лініям поля F, одночасно вказує шлях, правда не найкоротший, для знаходження цих поверхонь.

Приклад 1

z dx + (x – y) dy + zy dz = 0.

Умова (F • rot F) = 0, де F = zi + (x –y)j + yzk, не виконується, отже, дане рівняння не інтегрується одним співвідношенням.

Приклад 2

(6x + yz) dx + (xz - 2у) dy + (ху + 2z) dz = 0.

Так як rot F ≡ 0, де F = (6x + yz) i + (xz - 2y) j + (xy + 2z) k, то F = grad U, де

.

В якості шляху інтегрування вибираємо ламану, ланки якої паралельні осям координат. Інтегруючи, отримуємо U = 3x² – y² + z² + xyz, і отже, шуканим інтегралом є

3x² – y² + z² + xyz = с.