МСиС пособие

0,5. Изменение температуры вызывает смещение нуля потенциометра на Т= = 0,1 % /10 С. Нормальные условия эксплуатации потенциометра 20 2 С, потенциометр стоит в помещении, температура которого меняется от 8 до 32 С. Нормальные условия для напряжения питания Uн=200 В 2 %, а в реальных условиях эксплуатации напряжение может меняться на 10 % Uн. Напряжение наводки в линии связи частотой 50 Гц может достигать 1 мВ.

Решение

1 Основная погрешность аналогового регистратора определяется его классом точности. Погрешность всех электроизмерительных приборов согласно стандарту нормируется с 25 %-м запасом на старение, т.е. фактически погрешность нового прибора составляет не больше, чем 0,8 . Следовательно, рег = =0,8 0,5=0,4 (%).

2 У потенциометра преобладающей является погрешность дискретности, обусловленная конечным числом витков обмотки датчика, по которым скользит подвижный контакт. Эта погрешность имеет равномерное распределение. В этом случае рег =0,4 (%) можно считать половиной ширины этого равномерного

3 Погрешность от колебаний напряжения питания распределена по треугольному закону с принятыми пределами 10 %. Поэтому максимальное зна-

4 Погрешность наводки распределена арксинусоидально. Энтропийный коэффициент k=1,11. Тогда

нав. 1/200 100 0,450(%). 1,11

5 Погрешность смещения нуля потенциометра при колебании температуры является аддитивной, а закон ее распределения можно считать равномерным со средним значением 20 С и размахом 12 С (так как температура в помещении меняется от 8 до 32 С). Максимальное значение этой погрешности при Т=

= 0,1 % /10 С составляет T 0,1 12 0,07%, так как kэ для равномерного

10 3

распределения равен3.

14

6 Суммирование погрешностей сводится к вычислению приведенной погрешности при х = 0, которая складывается из всех аддитивных составляющих, и в конце диапазона, которая складывается из всех составляющих.

При х=0 погрешность будет складываться из трех составляющих:

п=0,24 %, Т=0,07 %, нп=1,30 %.

Однако т =0,07 % меньше нп =1,3 % в 18,5 раз. Так как суммирование под корнем будет производиться над квадратами величин, то ее вклад в результат будет ничтожным. Отсюда ясно, что этой погрешностью можно пренебречь и опустить из дальнейшего рассмотрения. Тогда

н п2 нп2 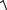0,242 1,302 1,32(%).

Для расчета погрешности в конце диапазона к полученному значению н надо добавить погрешность наводки нав.= 0,45 %:

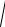к нав2 . н2 0,452 1,322 1,39(%).

Для перехода к интервальной оценке в виде доверительного д = t или энтропийного э = k значений необходимо знание не самого закона распределения результирующей погрешности, а лишь его одного числового параметра в виде квантильного множителя t или энтропийного коэффициента k .

Зависимости энтропийного коэффициента k от соотношения суммируемых составляющих и их энтропийных коэффициентов могут быть представлены в виде семейства графиков (график 1 и график 2).

По оси абсцисс отложены значения относительного веса дисперсии 22 вто-

рого из суммируемых распреде-лений в полной дисперсии p 22 /( 12 22), по оси ординат – значение энтропийного коэффициен-та k образующейся при этом ком-позиции. Кривая 1 соответствует композиции двух нормальных распределений (k = 2,066 для любых значений веса р); кривая 2 – композиции равномерно распределенной и нормально распределенной погрешностей; кривая 3 – композиции двух равномерных распределений; кривая 4 –композиции арксинусоидальной и равномерно распределенной погрешностей; кривая 5 –для двух арксинусоидально распределенных погрешностей.

Кривые 1-3 соответствуют сумми-рованию равномерного, треугольного и нормального распределений с дискретным двузначным распре-делением, а кривые 4-6 – суммированию нормального распределения соответственно с арксинусоидальным, равномерным и экспоненциальным.

15

1,32

1,32 0,242 0,98. Так как нп распределена по треугольному закону, а п – по равномерному (кривая 2 на графике 2). Отсюда k н 1,25.

Тогда при х=0 доверительные границы

н k н н =1,25 1,3=1,63 (%)

Вконце диапазона весовой коэффициент нав. в полной дисперсии равен

Поскольку нав. распределена по арксинусоидальному, а н – по нормальному законам, воспользуемся кривой 4 на графике 2.

k к 2,066.

Тогда в конце диапазона доверительные границы k k k k =2,066 1,39= =2,87 (%).

Задачи для самостоятельного решения

Задача № 1

В процессе однократного измерения индуктивности катушки получено значение L = 154 мГн и tg = 0,5. Из технических характеристик прибора известно, что основная погрешность измерения индуктивности не превышает = [(1 + + tg ) Lx 10 3+ 0,1 мкГн + Lк 10 3], где Lк - конечное значение предела измерения (Lк = 1000 Гн). Прибор находится в помещении, где температура колеблется

16

от 15 С до 25 С. Определить погрешность измерения индуктивности катушки при доверительной вероятности Р = 0,99.

Задача № 2

На основании предварительных измерений напряжения известно среднеквадратическое отклонение результата измерения U = 0,51 В; границы неис-

ключенных остатков четырех составляющих систематической погрешности

c1 = 0,39 В; c2 = 0,81 В; c3 = 0,24 В; c4 = 0,55 В. Определить доверитель-

ные границы погрешности измерения напряжения U = 81,48 В с однократным наблюдением. Доверительная вероятность Р = 0,95.

Задача № 3

Для измерения энергии, потребляемой нагрузкой на постоянном токе за время t, использовался косвенный метод и выражение U2t/R. При этом в результате однократных измерений были получены следующие значения:

-напряжение U = 146 В с погрешностью 20 В;

-сопротивление нагрузки R=415 Ом с погрешностью 5 Ом;

-время t=15 с с погрешностью 0,04 с;

границы неисключенных остатков трех составляющих систематической по-

грешности cU 0,44B; cR 0,15Ом; Rct 0,48c.

Оценить суммарную погрешность измерения энергии и записать результат с доверительной вероятностью Рд=0,99.

3 ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ НАБЛЮДЕНИЙ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ

Рекомендуемая литература: [3, с.26-31, 35-37], [4, с.10-36], [8, с.120-125], [9].

Методические указания При изучении темы необходимо:

-изучить и точно знать, какие измерения являются прямыми и какие погрешности измерений относят к систематическим, случайным и грубым;

-рассмотреть способы оценки и уменьшения систематических погрешностей, обратив особое внимание на правила суммирования неисключенных систематических погрешностей;

-ознакомиться с основными выражениями математического описания случайных погрешностей (среднее арифметическое, дисперсия, среднее квадратическое отклонение);

-изучить основные теоретические положения и алгоритмы обработки результатов многократных прямых равноточных и неравноточных измерений;

-знать правила и формы представления погрешностей и записи результатов измерений.

Контрольные вопросы 1 Какие измерения называются прямыми?

17

2 Какие измерения относят к равноточным, а какие к неравноточным?

3 В зависимости от чего применяют однократные либо многократные наблюдения?

4 Перечислите основные признаки, по которым классифицируются погрешности измерений.

5 Какие существуют методы обнаружения и оценки систематических погрешностей?

6 Сформулируйте правила суммирования систематических погрешностей.

7 Как оценивается случайная погрешность результатов прямых измерений? Приведите необходимые математические соотношения.

8 Опишите алгоритмы обработки прямых равноточных измерений.

9 Поясните суть критерия грубых погрешностей.

10 В каких случаях используются точечные и интервальные оценки погрешностей измерений?

Общие положения алгоритма обработки результатов многократных наблюдений при прямых измерениях

1 При статистической обработке группы результатов наблюдений следует выполнить следующие операции:

-исключить известные систематические погрешности из результатов наблюдений;

-вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;

-вычислить оценку среднего квадратического отклонения результата измерения;

-проверить гипотезу о том, что результаты измерений принадлежат к нормальному распределению;

-вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;

-вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;

-вычислить доверительные границы суммарной погрешности результата измерения.

2 Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости q от 10 до 2

%.Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.

3 Для определения доверительных границ погрешности результата измерения доверительную вероятность P принимают равной 0,95. В тех случаях, когда измерения нельзя повторить, и других особых случаях, результаты которых имеют важное значение, допускается указывать границы для доверительной вероятности Рд = 0,99.

18

Решение типовых задач

Задача № 1

Обработать ряд результатов наблюдений Xi (таблица 1), полученный по результатам многократных прямых измерений сопротивления, и оценить случайную погрешность измерения, считая результаты исправленными и равноточными. Доверительную вероятность принять Рд = 0,95. Результат измерения представить по одной из форм, предусмотренных ГОСТ 8.207-76.

Таблица 1

1 Так как в условии задачи указано, что результаты измерения являются исправленными и равноточными, то производить исключение систематических погрешностей нет необходимости.

2 Вычисляем среднее арифметическое результатов наблюдений

19

Продолжение таблицы 2

n

Правильность вычислений Х и Vi определяем по формуле Vi 0. Если

i 1

n

Vi 0, то имеют место ошибки в вычислениях.

i 1

4 Вычисляем оценку среднего квадратического отклонения результатов наблюдений x

5 С помощью критерия грубых погрешностей (критерий «трёх сигм») проверяем наличие грубых погрешностей.

В соответствии с этим критерием, если |Vi | 3 x , то такое наблюдение содержит грубую погрешность. В случае обнаружения грубой погрешности в i-м наблюдении необходимо это наблюдение исключить из результатов наблюдений и повторить вычисления по пп. 1-5 для меньшего числа n.

В решаемой задаче 3 x 3 0,105 0,315 кОм и, как видно из таблицы 2, грубые погрешности отсутствуют.

6 Определяем оценку среднего квадратического отклонения результата измерения x из выражения

7 Выдвигаем гипотезу о принадлежности результатов наблюдений нормальному распределению и проверяем эту гипотезу.

20

а) При числе результатов наблюдений n > 50 для проверки принадлежности их к нормальному распределению в соответствии с ГОСТ 11.006-74 предпочти-

тельным является один из критериев 2 Пирсона или 2 Мизеса-Смирнова. При числе результатов наблюдений 50>n>15 для проверки принадлежности

их к нормальному распределению предпочтительным является составной критерий, приведённый в [9].

При числе результатов наблюдений n 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной [1], возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению. Если условие принадлежности результатов наблюдений нормальному распределению не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

В решаемой задаче n = 25. Поэтому принадлежность результатов наблюдений к нормальному распределению проверяем по составному критерию.

б) Критерий 1. Вычисляем смещённую оценку среднего квадратического отклонения по формуле

Результаты наблюдений можно считать распределенными нормально, если

d1 q /2 d dq /2,

1 1

где d1 q1 /2 и dq1 /2 - квантили распределения, получаемые из таблицы 3

по n, q1/2 и (1 - q1/2), причем q1 - заранее выбранный уровень значимости критерия.

Выбираем уровень значимости q равным 5 %. Из таблицы 3 находим dq1 /2=

нами, делаем вывод о том, что по критерию 1 результаты наблюдений распределены по нормальному закону.

Критерий 2. Этот критерий используется дополнительно для проверки «концов» распределений.

21

Гипотеза о нормальности по критерию 2 не отвергается, если не более m разностей Vi превзошли значение ZP/2 x , где верная квантиль распределения

нормированной функции Лапласа отвечает вероятности P/2. Tаблица 3 - Статистика d

Таблица 4 - Значения P для вычисления ZP/2.

Значения P определяются из таблицы 4 по выбранному уровню значимости q2 и числу результатов наблюдений, а значения ZP/2 - из таблицы 5.

Для решаемой задачи выбираем уровень значимости q2 = 5% и для n = 25 из таблицы 4 находим P = 0,97 и m = 2. Тогда, обращаясь к таблице 5, находим ZP/2

= 2,17. Отсюда

ZP/2 x = 0,229 кОм.

Согласно критерию 2 не более двух (m = 2) разностей Vi могут превзойти значение 0,229 кОм.

По данным, приведенным в таблице 2, видим, что только V12 превышает критическое значение. Следовательно, критерий 2 выполняется.

Таким образом, с уровнем значимости q q1+ q2 = 0,1 гипотеза о нормальности полученных данных согласуется с данными наблюдений.

22

Таблица 5 - Значения нормированной функции Лапласа ф(z).

8 По заданной доверительной вероятности Pд и числу степеней свободы (n 1) распределения Стьюдента определим коэффициент t из таблицы 6.

Для нашей задачи (P = 0,95 и n-1 = 24) значение t = 2,064.

Рассчитываем доверительные границы случайной погрешности результата измерения

t x 2,064 0,021 = 0,043 кОм.

23