
- •Работает
- •1.1. История создания эвм.
- •1.3. Размещение данных и программ в памяти пэвм.
- •1.4.Файловая система хранения информации
- •1.5.Операционная система.
- •Лекция 2. Как составляются и выполняются программы в системе delphi
- •2.1. Понятие алгоритма и способы его записи
- •2.2. Общая характеристика языка Паскаль
- •2.3. Как составляется программа в системе Delphi
- •2.4. Наша первая программа реализует линейный алгоритм
- •3.1. Данные и их типы.
- •3.2. Операции над переменными основных скалярных типов
- •Алгоритмов
- •4.1. Понятие разветвляющегося алгоритма
- •4.2. Оператор условия if
- •4.3. Оператор выбора Case
- •4.4. Некоторые возможности, предоставляемые Delphi для организации разветвлений
- •Лекция 5. Составление и програмирование циклических алгоритмов
- •5.1. Понятие цикла
- •5.2. Оператор Repeat...Until
- •5.3. Оператор While...Do
- •5.4. Оператор For...Do
- •5.5. Вложенные циклы
- •5.6. Примеры некоторых часто встречающихся циклических алгоритмов Вычисление заданного члена рекуррентной последовательности
- •Вычисления сумм с использованием рекуррентной последовательности
- •6.1. Ошибки на этапе компиляции
- •6.4. Защищенные блоки
- •6.5. Некоторые стандартные типы исключительных ситуаций
- •6.6. Инициирование собственных исключительных ситуаций
- •6.7. Примеры фрагментов программ
- •Лекция 7. Составление программ с использованием массивов
- •7.1. Понятие массива
- •7.2. Некоторые возможности ввода-вывода в Delphi
- •7.3. Примеры часто встречающихся алгоритмов работы с массивами Сумма n элементов одномерного массива:
- •Произведение диагональных элементов квадратной матрицы:
- •Нахождение максимального элемента одномерного массива:
- •8.1. Статическое и динамическое распределение оперативной памяти
- •8.2. Понятие указателя
- •8.3. Наложение переменных
- •8.4. Динамическое распределение памяти
- •8.5. Организация динамических массивов
- •9.1. Понятие подпрограммы
- •9.2. Описание подпрограмм
- •9.3. Передача данных между подпрограммой и вызывающей ее программой
- •9.4. Оформление подпрограмм в библиотечный модуль
- •9.5. Примеры подпрограмм, оформленных в отдельные библиотечные модули
- •Пример программы, использующей модуль RabMas:
- •Множества
- •10.1. Понятие множества
- •10.2. Операции над множествами
- •10.3. Примеры работы с множествами
- •Interface
- •11.1. Зачем нужны строки
- •11.2. Описание переменных строкового типа «Короткие строки»
- •11.3. Основные операции над переменными строкового типа
- •11.4. Некоторые процедуры и функции обработки строк
- •11.5. Примеры алгоритмов обработки строк
- •Лекция 12. Программирование с использованием записей
- •12.1. Понятие записи
- •12.2. Операции над записями
- •12.3. Использование записей для работы с комплексными числами
- •13.1. Понятие файла
- •13.2. Операции над файлами
- •13.2.1. Типизированные файлы
- •13.2.2. Текстовые файлы
- •13.3. Подпрограммы работы с файлами
- •13.4. Компоненты tOpenDialog и tSaveDialog
- •Лекция 14. Программирование с отображением графической информации
- •14.1. Как рисуются изображения
- •14.2. Построение графиков с помощью компонента tChart
- •Лекция 15. Программирование с использованием рекурсии
- •15.1. Понятие рекурсии
- •15.2. Примеры рекурсивных вычислений
- •16.1. Организация работы с базами данных
- •16.2. Поиск в массиве записей
- •16.3. Сортировка массивов
- •16.3.1. Метод пузырька
- •16.3.2. Метод прямого выбора
- •16.3.3. Метод Шелла
- •16.3.4. Метод Хоара (Hoare)
- •17.1. Работа со списками
- •17.2. Добавление нового элемента в список на заданную позицию
- •17.3. Удаления элемента с заданным номером
- •17.4. Пример программы
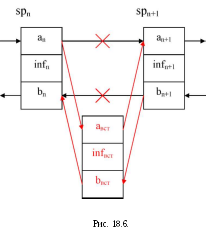
- •Лекция 18. Связанные списки на основе рекурсивных данных
- •18.1. Что такое стек и очередь
- •18.2. Понятие рекурсивных данных и однонаправленные списки
- •18.3. Процедуры для работы со стеками
- •18.4. Процедуры для работы с односвязными очередями
- •18.5. Работа с двухсвязными очередями
- •18.6. Процедуры для работы с двусвязными очередями
- •19.1. Основные понятия и определения
- •19.2. Прямые методы решения слау
- •19.3. Итерационные методы решения слау
- •20.1. Зачем нужна аппроксимация функций?
- •20.3. Какие бывают многочлены и способы интерполяции?
- •20.4. Что такое среднеквадратичная аппроксимация?
- •20.5. Метод наименьших квадратов (мнк)
- •21.1. Формулы численного дифференцирования
- •21.2. Формулы численного интегрирования
- •22.1. Как решаются нелинейные уравнения
- •22.2. Итерационные методы уточнения корней
- •22.2.2. Метод Ньютона
- •23.1. Постановка задач оптимизации, их классификация
- •23.2. Методы нахождения минимума функции одной переменной
- •24.1. Задачи для обыкновенных дифференциальных уравнений
- •24.2. Основные положения метода сеток для решения задачи Коши
- •24.3. Многошаговые схемы Адамса
- •Литература
19.1. Основные понятия и определения
Выделяют четыре основные задачи линейной алгебры: решение СЛАУ, вычисление определителя матрицы, нахождение обратной матрицы, определение собственных значений и собственных векторов матрицы.
Задача отыскания решения СЛАУ с n неизвестными - одна из наиболее часто встречающихся в практике вычислительных задач, так как большинство методов решения сложных задач основано на сведении их к решению некоторой последовательности СЛАУ.
Обычно СЛАУ записывается в виде
n
^ciyXj = bi ;1 < i < n, или коротко
j=1
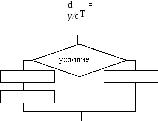
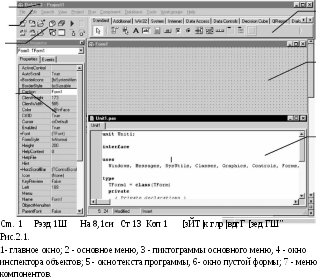
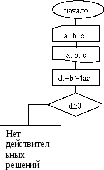
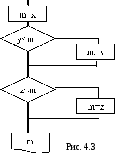
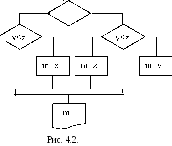
AX = b,
A =
x =
b =
(19.1)
Xi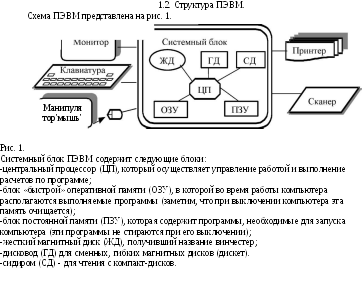





x
anlan 2...ann
Здесь А и b заданы, требуется найти X *, удовлетворяющий (19.1).
Известно, что если определитель матри-
— цы \A ф 0, то СЛАУ имеет единственное ре-xi
Рис 19 1 шение. В противном случае решение либо от-
сутствует (если b ф 0), либо имеется бесконечное множество решений (если b = 0). При решении систем, кроме условия |A| ф 0, важно
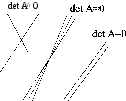
чтобы задача была корректной, т.е. чтобы при малых погрешностях правой части Ab и (или) коэффициентов Aa^ погрешность решения AX * также оставалась малой. Признаком некорректности, или плохой обусловленности, является близость к нулю определителя матрицы.
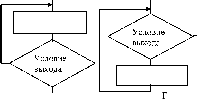
Плохо обусловленная система двух уравнений геометрически соответствует почти параллельным прямым (рис.19.1). Точка пересечения таких прямых (решение) при малейшей погрешности коэффициентов резко сдвигается. Обусловленность (корректность) СЛАУ характеризуется числом
X = |AI • A-1 > 1. Чем дальше х от 1, тем хуже обусловлена система. Обычно
при х > 10 система некорректна и требует специальных методов решения -методов регуляризации. Приведенные ниже методы применимы только для корректных систем.
Методы решения СЛАУ делятся на прямые и итерационные.
Прямые методы дают в принципе точное решение (если не учитывать ошибок округления) за конечное число арифметических операций. Для хорошо обусловленных СЛАУ небольшого порядка n < 200 применяются практически только прямые методы.
Наибольшее распространение среди прямых методов получили метод Гаусса для СЛАУ общего вида, его модификация для трехдиагональной матрицы - метод прогонки и метод квадратного корня для СЛАУ с симметричной матрицей.
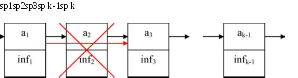
Итерационные методы основаны на построении сходящейся к точно-
му решению
X
рекуррентной
последовательности
векторов
x ■ x ■
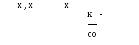 ->
x . Итерации
выполняют до тех пор, пока норма <
s. (г-
заданная
малая величина).
->
x . Итерации
выполняют до тех пор, пока норма <
s. (г-
заданная
малая величина).
Итерационные методы выгодны для систем большого порядка n>100, а также для решения плохо обусловленных систем. Многообразие итерационных методов решения СЛАУ объясняется возможностью большого выбора рекуррентных последовательностей, определяющих метод. Наибольшее распространение среди итерационных методов получили одношаговые методы простой итерации и Зейделя с использованием релаксации.
Для контроля полезно найти невязку полученного решения х:
max
1<к <n
I
aMxi
если А велико, то это указывает на грубую ошибку в расчете.
Ниже приведено описание алгоритмов указанных методов решения
СЛАУ.
