Введение в математический анализ

Лекция 9 Множества и операции над ними

Рассмотрим понятие множества. Можно говорить о множестве дней в году, точек на плоскости, студентов в данной аудитории и т.д. В этих случаях каждый день в году, каждая точка на плоскости, каждый студент в аудитории является элементом соответствующего множества.

Существенным обстоятельством при рассмотрении конкретного множества является возможность для всякого элемента дать вполне определенный ответ на вопрос – принадлежит ли данный элемент множеству или нет. Так для первого из приведенных выше множеств, 3 июля, 25 ноября, 9 января – элементы рассматриваемого множества, когда как «среда», «пятница», «праздник» не являются элементами рассматриваемого множества. Во втором примере элементами множества являются только точки заданной плоскости. Если точки не принадлежат заданной плоскости или рассматриваемый элемент не есть точка, то эти элементы не являются элементами множества.

Множеством М называется объединение в единое целое определенных различимых объектов а, которые называются элементами множества: а М.

Множество можно описать, указав какое–нибудь свойство, присущее всем элементам этого множества.

Множество, не содержащее элементов, называется пустым и обозначается .

Два множества A и B называются равнымиA = B , если они состоят из одних и тех же элементов.

Запись A ={a1,a2 ,a3 ,...} означает, что множество A состоит из элементов a1,a2 ,a3 ,... Если множество A состоит из тех элементов множества B , которые

Например множество точек отрезка [a,b] может быть записано следующим образом: A ={x \| a ≤ x ≤ b}.

Если все элементы множества А являются также элементами множества В, то говорят, что множество А включается (содержится) в множестве В.

А

В

А В

Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Венна.

81

подмножеством множества В и обозначается А В.

Два множества A и B равны тогда и только тогда когда справедливы соотношения: A B и B A.

Операции над множествами

Объединением (суммой) множеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А и В.

Обозначается С=А В.

А

В

Пересечением (произведением) множеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.

Обозначение С=А∩В.

АС В

Для множеств А, В и С справедливы следующие свойства:

A = А; A ∩ = ;

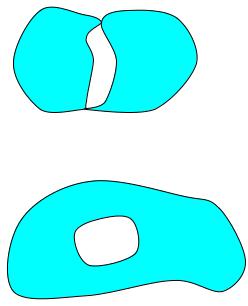
Разностью множеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Обозначается С=А\В.

АВ

82

Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.

Обозначается А ∆ В.

А ∆ В = (A \ B) (B \ A)

A B

СЕ называется дополнением множества А относительно множества Е, если А Е и CЕ = Е \ A.

A E

Для множеств А, В и С справедливы следующие соотношения:

Пример 1. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Венна A \ B = A \ ( A ∩ B) .

Решение. Из записанных выше соотношений видно, что

A \ ( A ∩ B) = ( A \ A) ( A \ B) = ( A \ B) = A \ B

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Венна

83

Пример 2. Исходя из определения равенства множеств и операций над множествами, доказать тождество A \ (B C) = (A \ B) ∩ (A \ C)

Решение. Если некоторый элемент х А \ (В С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А \ В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A \ B) ∩ (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

Отображения (функции)

Если для каждого x X по определенному правилу поставлен в соответствие элемент y Y , то говорят, что задана функция (отображение) f

y = f (x) ,–множеством значений функции.

В дальнейшем мы будем рассматривать так называемые однозначные числовые функции f: x X \ !y Y \: y = f (x) .

Графиком функции называется множество точек на декартовой плоскости с координатами (x, f (x)) .

Способы задания функций

Функция может быть задана:

1.Аналитически в виде комбинаций алгебраических действий и известных элементарных функций: xα ,ax , loga x, tgx, ctgx,sin x, cos x .

2.Графически

84