Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный экономический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lekcii.Vysshaya matematika (2 semestr).pdf

Скачиваний:

459

Добавлен:

20.02.2016

Размер:

2.84 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3110 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Лекция № 3

Функции многих переменных

проф. Дымков М. П.

4.2. Дифференцируемость функции многих переменных

Частные производные.

Пусть функция z = f (x, y) определена в области D R2 и точка M 0 (x0 , y0 ) D.

Определение 4.9. Частным приращением функции z по

переменной

в точке

называется разность

M 0

∆

f (x

0 +

∆

x, y0 ) − f (x0 , y0 )

(4.1)

x z

Определение 4.10. Частной производной функции

z = f (x, y)

по переменной

в точке

M 0 (x0 , y0 )

называется

предел (

если

он

существует)

частного

отношения

приращения

функции

по

к вызвавшему его

приращению независимой переменной

∆

, когда ∆

→ 0

∆ x z

fx′(x0 , y0 )

lim

(4.2)

∆ x

Ä x→0

Частная производная по x в точке M 0 (x0 , y0 ) обозначаетсялюбымизследующихспособов:

∂z		,	∂f (x0 , y0 ) , z′x	,	fx′(x0 , y0 ) .
∂z		,	∂f (x0 , y0 ) , z′x	,	fx′(x0 , y0 ) .
∂x	M 0		∂x	x = x0 , y = y0

Аналогично определяется частная производная функции

z = f (x, y)			по переменной y :
∂f (x	, y	)	= lim	∆ y z	,
0	0
				∆ y
∂y			Ä y→0
где	∆y z = f (x0 , y0				+ ∆y) − f (x0 , y0 ).	(4.3)

Лекция № 3

Функции многих переменных

проф. Дымков М. П.

пространстве XYZ условие

y = y0

описывает плоскость P, перпендикулярную

оси OY и пересекающую эту ось в точке y0.

Плоскость P пересекается с графиком

функции z = f(x,y), вдоль некоторой линии L,

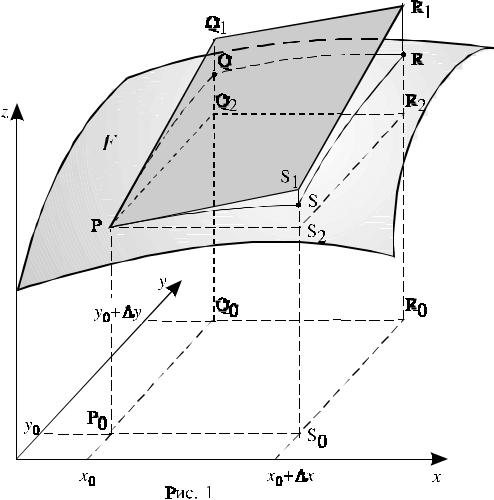
как показано на рисунке 1. Тангенс угла

между плоскостью XOY и касательной к

линии L в точке с координатами x0,y0 равен

частной производной по x функции z = f(x,y) в

этой точке. В этом состоит геометрический

смысл частной производной.

Пример 4.3. Вычислить по определению частные

производные функции

z = x2 −3xy + 2 y2

в точке M 0 (1,2) .

Решение.

Имеем

f (x, y) = x2

−3xy + 2 y2 , f (x0 , y0 ) = f (1,2) =

=12 −3 1 2 + 2 22 = 3;

f (x0

+∆x, y0 ) = f (1 + ∆x,2) = (1 + ∆x)2 +

3(1 +∆x)2+ 2

2 = 3 − 4∆x + ( ∆ x)2 ;

∆x z = f (x0 +∆x, y0 ) − f (x0 , y0 ) =3 − 4 ∆x +(∆x)2 −3 = − 4 ∆x +(∆

x)2
Тогда, согласно (4.2), имеем:
∂	= lim	− 4∆ x + (∆ x)2	= lim		(−4 + ∆ x) = −4 .
z	= lim	∆ x	= lim		(−4 + ∆ x) = −4 .
∂x	Ä x→0	∆ x		Ä x→0
	Ä x→0			Ä x→0

M 0

Аналогично вычисляем

∆y z = f (x0 , y0 +∆y) − f (x0 , y0 ) = f (1,2 +∆y )− 3 =12 −3 1(2 +

∆y) + 2 (2 +∆y)2 −3 =1−6 −3∆y +8 +8∆y + 2( ∆y)2 −3 = 5

∆y + 2 ( ∆y)2 .

Тогда, согласно (4.3)

∂z(M 0 )	= lim	∆y z
∂y		∆ y
	Ä y→0

, имеем:
= lim	5∆y + 2(y)2	=	lim (−5 + 2 ∆y) = 5.
Ä y→0	∆ y		Ä y→0
Ä y→0

Лекция № 3	Функции многих переменных		проф. Дымков М. П.			9

	Для нахождения частных производных функции
z = f (x, y)	следует запомнить		правило:	при вычислении
	производной по	x	считаем	y	постоянной	и
частной

пользуемся правилом дифференцирования функции одной независимой переменной; при вычислении частной производной по y считаем x постоянной и пользуемся этими

же правилами дифференцирования (производная постоянной равна нулю; постоянный множитель выносится за знак производной и т.д.).

Пример 4.4. Вычислить частные производные

∂z

и ∂z в

M (x, y)

∂x

∂y

произвольной

точке

для

функции

f (x, y) = x

−3xy + 2 y

и затем найти их значения

∂z(M 0 )

∂x

и ∂z(M 0 )

, если

M 0 (1,2) .

∂y

∂z

Решение. Имеем :

=(x

−3xy + 2 y

2 ′

∂x

)x, y−const =

= (x2 )′x, y−const

−(3xy)′x, y−const

+(2y2 )′x, y−const = 2x − 3y(x)′ + 0 = 2x − 3y .

Тогда

∂z (1,2) =2 1 −3 2 = −4.

∂x

∂z

=(x

−3xy + 2 y

2 ′

= (x

′

−const −

′

∂y

)y,x−const

)y ,x

(3xy)y,x−const +

+ (2 y

′

∂z

(1,2) = − 3 1 + 2

4 = 5.

)y,x−const = 0 −3x + 4 y . Значит,

∂y

Лекция № 3 Функции многих переменных проф. Дымков М. П. 10

Аналогично (4.2) и (4.3)

определяются частные производные

∂z

…,

∂z

для

многих переменных

z = f (x , x ,..., x )

∂xn

∂x1

∂x2

1 2

Например,

∂z

lim

∆x z

(4.4)

∂x

Äx1→0

∆ x

Отметим очень важное отличие функции двух переменных от функции одной переменной. ♣

Из существования первых частных производных в точке не следует непрерывность функции в этой точке.

Рассмотрим, например, функцию

( ) 0 при xy = 0 f x, y = 1 при xy ≠ 0 .

График этой функции во всех точках, не принадлежащих осям координат OX и OY, представляет собой плоскость, параллельную плоскости XOY, поднятую на 1. Сами эти оси координат также принадлежат графику рассматриваемой функции. Очевидно, что в точке (0,0) функция имеет частные производные по обоим аргументам, обе равные нулю. Очевидно также, что в любой окрестности точки (0,0) можно найти точку M такую, что f(M) = 1, в то время как f(0, 0) = 0. Это означает существование разрыва функции в точке (0,0).

Лекция № 3 Функции многих переменных

проф. Дымков М. П.

4.2.2. Дифференцируемые функции.

Определение 4.11. Полным приращением функции

z = f (x, y)

в точке

M 0 (x0 , y0 )

называется разность

∆

z(M0 )

f (x0 +

∆

x, y0

∆

y) − f (x0, y0 )

(4.5)

Определение 4.2.

Функция

z = f (x, y)

называется

дифференцируемой в точке

M 0

, если в некоторой

окрестности этой точки полное

приращение

функции можно

представить в виде :

∆

(M 0 ) = A(x0, y0 )

∆

B(x0 , y0

) ∆y+

x +

+α 1(

∆

x +

α 2(

∆

(4.6)

где коэффициенты

A(x0, y0 )

B(x0, y0 )

не зависят от ∆

и ∆

а функции

α1 (

∆

∆y) и

α 2(

∆

∆y) являются

бесконечно

малыми при условии, что

величина

ñ =

(∆ x)2

+ (∆

y)2

стремится к нулю.

Пример 4.5. Показать, что функция z = x2

+ 3xy является

дифференцируемой в любой точке

M 0 (x0, y0 ).

Решение. Имеем: f (x, y) = x2 + 3xy, f (x0, y0 ) = x0

2 +3x0 y0 ,

f (x0 +∆x, y0 +∆y) = (x0 +∆x)2 + 3(x0 +∆x) ( y0 + ∆y) =

= x 2

+ 2x ∆x + ( ∆x)2 +3x y

+3x ∆y + 3∆xy

+ 3∆x ∆y .

Тогда по (4.5) полное приращение ∆ z

имеет вид :

∆z(x , y

)=x 2

+ 2x ∆x +∆x2 +3x

+3x

∆y + 3∆xy + 3∆x∆y −

− x0 2 −3x0 y0 =(2x0 + 3y0 ) ∆x + 3x0 ∆y + ∆x ∆x + 3∆x ∆y .

Сравнивая с (4.6), заключаем, что

A(x0 , y0 ) = 2x0 + 3y0 ,

B(x0 , y0 ) = 3x0 ,

α 1(∆x,∆y) =∆x,

α 2(∆x,∆y) =3∆x .

Лекция № 3

Функции многих переменных

проф. Дымков М. П.

Значит, функция является дифференцируемой в т. M 0 (x0, y0 ).

Теорема 4.7. Если функция z = f (x, y) дифференцируема в

точке M 0 (x0, y0 ), то она непрерывна в этой точке и имеет в ней

частные производные по всем аргументам : ∂f (M 0 ) , ∂f (M 0 ) .

∂x ∂y

Приведенная теорема показывает, что взаимоотношение непрерывности и дифференцируемости функции в многомерном случае такое же, как в одномерном. Совсем иначе обстоит дело во взаимоотношениях частных производных и дифференцируемости. В случае одной переменной дифференцируемость и наличие производной были условиями равносильными.

Для

функций

многих

переменных

наличие

частных

производных

не гарантирует дифференцируемость. ♣

Однако уже непрерывность частных производных

обеспечивает дифференцируемость.

Теорема 4.8. Если в некоторой окрестности точки

существуют

частные производные

∂z (x, y)

(x y

)

∂x

и они непрерывны в точке

∂z (x, y)

, то функция

(x y

)

∂y

дифференцируема в точке

z = f (x, y)

M0 (x0, y0 )

4.2.3. Полный дифференциал функции многих переменных.

Определение 4.13.		Если функция				z = f (x, y)
дифференцируема в точке		M 0 (x0, y0 )		,	то	линейная
относительно приращений ∆	x				часть	полного
относительно приращений ∆	x	и ∆	y		часть	полного

приращения функции называется полным дифференциалом функции z = f (x, y) в точке M 0 (x0, y0 ) и обозначается dz(M0 ) :

Лекция № 3		Функции многих переменных								проф. Дымков М. П.	13

			=	∂z(M 0 )	∆		∂z(M 0 )	∆	y		(4.7)
	dz(M 0 )
						x +
				∂x			∂y
				∂x			∂y

Если принять по определению за дифференциалы независимых переменных x и y их приращения ∆x и ∆y , т.е. положить dx = ∆x и dy = ∆y , то (4.7) примет вид :

	=	∂z(M 0 )			∂z(M 0 )		y	(4.8)
dz(M 0 )
			d			d
				x +
		∂x			∂y

Пример 4.6.

Найти полный дифференциал функции z = ln(x2 + y2 ) в

точке M 0 (1,2) .

Решение. Имеем

∂z

=(ln(x

+ y

′

∂x

))x, y−const =

(x2

+ y2 )′x

. Тогда

∂z

2 1

. Далее

x2 + y2

+ y2

∂x

12 + 22

находим

2 y

∂z

(ln(x

+ y

′

,x−const =

+ y

2 ′

))y

. Тогда

∂y

x2 + y2

+ y2

∂z

2 2

Согласно (4.8) получаем полный

∂y

12 + 22

дифференциал

dz(M 0 ) = 0,4dx + 0,8dy .

Лекция № 3

Функции многих переменных

проф. Дымков М. П.

На рисунке график функции z = f(x,y) представляет собой поверхность F. Длина отрезка Р0Р равна значению функции z в точке P0, то есть Р0Р = f(x0,y0)

Координатами точек Q0, S0 и R0 являются (x0,y0+∆у); (x0+∆x,y0)

и (x0+∆x,y0+∆у), причём Q0Q = f(Q0), S0S = f(S0) и

R0R = f(R0). Приращение ∆f(х0,у0) функции в точке Р0 равноRR2 . Параллелограмм PQ1R1S1 лежит в плоскости, которая касается поверхности F в точке Р. Прямоугольник PQ2R2S2 расположен в горизонтальной плоскости.

Очевидно: Q2Q1 = f′y(x0,y0)∆y и S2S1 = f′x(x0,y0)∆x. Из легко доказываемого равенства R2R1 = S2S1 + Q2Q1 и

Лекция № 3 Функции многих переменных проф. Дымков М. П. 15

формулы (4.8) следует, что дифференциал функции в точке Р0


равен отрезку R2R1 ,		т.е .	df(x0,y0) = R2R1 .
4.2.4.	Приложения		полного	дифференциала	в
приближенных		вычислениях

Справедлива формула приближенного вычисления значений функции:

f (x0 + ∆x, y0 + ∆y) ≈ f (x0 , y0 ) + ∂∂fx (x0 , y0 ) ∆x + ∂∂fy (x0 , y0 ) ∆y

или

df(x0,y0) ≈ ∆f(x0,y0).

Пример. 4.7. Вычислить приближенно 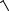4,032 + 2,992 . Решение. Рассмотрим функцию z = f (x, y) = x2 + y2 .

Тогда искомое число есть значение этой функции в точке

x = x0

+ ∆x = 4,03,

y = y0

+ ∆y = 2,99. Выбирая x0 = 4, y0 = 3,

получим

∆x = 0,03;

∆y = −0,01. Далее находим

значения

функции и

ее частных

производных

в точке

M (x0 , y0 ) :

f (x0 , y0 ) = 42 + 32 = 5,

∂f

, y

) =

∂f

, y

) =

2 y

∂x

2 x2 + y2

∂y

2 x2 + y2

x = 4,

y = 3

Тогда

4,032

+ 2,99

2 ≈ 5 + 4

0,03 + 3 (−0,01) = 5,018.

4.2.5. Производные высших порядков.

Пусть

функция

имеет

частные

производные

z = f (x, y)

∂z

= f ′(x, y)

∂z

= f ′(x, y)

где (

некоторая

x, y) D

D −

∂x

∂y

подобласть

области

на

которой

определена

функция

Лекция № 3	Функции многих переменных					проф. Дымков М. П.			16
	. Значит, на			заданы две новые функции					двух
		D1
z = f (x, y)
переменных	, а именно		u	= ∂z (x, y)	и	v = ∂z (x, y)	и можно
				∂x		∂y		x		y
находить их частные производные					по				и		.
						переменным

Эти частные производные и называются частными производными второго порядка или вторыми частными

производными функции

Итак, по определению:

z = f (x, y)

∂2 z

∂

(

∂z ) =

fxx

″(x, y)

;

∂2 z

∂

(∂z )

= fxy″(x, y)

∂x2

∂x

∂x∂y

∂x

∂y

∂2 z

∂

(∂z )

f yx″(x, y)

∂2 z

∂

(

∂z )

= fyy″(x, y)

∂y∂x

∂y

∂y2

∂x

∂y

причем,

частные производные

∂2 z

называются

∂x∂y

∂y∂x

смешанными частными производными.

Пример 4.8. Найти все частные производные второго

порядка функции z = x3 y3 .

Решение.

∂z

2 ′

′

= 3x

;

∂x

)x, y−const = y

∂z = (x3 y2 )′y,x−const = x3 ( y2 )y′ = x3 2 y = 2x3 y ;

∂y

∂2 z

∂

(

∂z ) =

∂

(3x2 y2 ) = y2 (3x2 )x′ = y2 6x = 6xy2 ;

∂x2

∂x

∂2 z

∂

(

∂z ) =

∂

(2x3 y) = 2x3 ;

∂y2

∂y

∂2 z

∂

(

∂z ) = =

∂

(2x3 y) = y

2 3 x2 =6x2 y ;

∂x∂y

∂x

∂y

∂2 z

∂

(

∂z ) ==

∂

(3x2 y2 ) = 3x2 2 y = 6x2 y =6x2 y ;

∂y∂x

∂y

∂x

Условия, при которых результат

дифференцирования не

зависит от порядка дифференцирования.♣

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 3110 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019117.76 Кб10Lek-07-1C_8_2-20.doc
#
24.09.201976.29 Кб9Lek-08-1C_8_2-80.doc
#
24.09.201994.72 Кб9Lek-09-1C_8_2-Свод.doc
#
24.09.2019441.34 Кб10Lek-10-Гал_8.10-Опис.doc
#
20.02.20162.06 Mб258Lekcii.Vysshaya matematika (1 semestr).pdf
#
20.02.20162.84 Mб459Lekcii.Vysshaya matematika (2 semestr).pdf
#
20.02.2016744.96 Кб59lekcii_marketingovye_issledovaniya.doc
#
20.02.2016610.3 Кб35lekcii_nac_ekonomika_rb.doc
#
20.02.2016645.12 Кб26lekcii_nac_ekonomika_rb.doc
#
20.02.201610.32 Mб239lekcii_po_makroekonomike.doc
#
20.02.201674.75 Кб6lektion 6 landeskunde.doc