
Часть1
.pdf
действующие на систему внешние силы: силы тяжести P1 , P2 , P3 и реакцию
направляющих |
N |
. Запишем уравнение движения центра |
масс системы в |
||||||||
векторной форме: |
|
||||||||||
|
|
M aC = |
|
|
|
|
|
|
|
|
(1) |
|
|
P1 + P2 + P3 + N . |
|||||||||
Проведем координатные оси Oxy так, чтобы ось y проходила через точку C30, где находился центр масс плиты в момент времени t0=0.
а) Определение перемещения x3(t) (вторая задача динамики). Для
определения x3 = f3 (t) спроектируем уравнение (1) на ось x. Получим |
|
||
&& |
e |
&& |
(2) |
M xC |
= åFkx |
или M xC = 0, |
|
так как все внешние силы перпендикулярны оси x и поэтому åFkxe = 0 . |
|||
Отметим также, что VCx = 0 |
при t = 0. Поэтому, интегрируя дважды уравнение |
||
(2), получим: |
M xC = const |
(3) |
|
|
|||
(закон сохранения координаты центра масс системы). Из (3) следует, что |
|||
|
M xC (t) = M xC (0) . |
(4) |
|
Определим значение |
M xC (t). |
Координата xC центра масс |
системы |
определяется по формуле |
|
|
|
M xC = m1x1 + m2 x2 + m3 x3 . |
(5) |
||
Из рис. Д2 видно, что в произвольный момент времени абсциссы грузов равны соответственно x1 = x3 − R cosϕ1, x2 = x3 + r sin ϕ2 . Подставляя эти выражения в
формулу (5) и учитывая заданные зависимости ϕ1 и ϕ2 от t, получим |
|
M xC (t) = (m1 + m2 + m3 )x3 (t) − m1R cos(πt) + m2r sin(π 2 − πt 2). |
(6) |
Определим значение M xC (0) . Подставляя в (6) t=0, x3(0)=0, получим |
|
M xC (0) = −m1R + m2r . |
(7) |
Всоответствии с уравнением (4), приравниваем правые части (6) и (7):
−m1R + m2r = (m1 + m2 + m3 )x3 − m1R cos(πt) + m2r cos(πt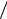 2).
2).
Отсюда получаем зависимость от времени координаты x3.
Ответ: x3 = 0,09[3cos(πt) − 2cos(πt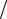 2)−1] м, где t – в секундах.
2)−1] м, где t – в секундах.
б) Определение реакции N (первая задача динамики). Для определения
N = f (t) |
спроектируем векторное уравнение (1) |
на вертикальную ось y (см. |
|||
рис. Д2): |
|
e |
|
|
|
|
&& |
&& |
|
(8) |
|
|
M yC |
= åFky |
или MyC = N − P1 − P2 − P3 . |
||
Отсюда получим, учитывая, что P1=m1g, и т.д.: |
|
(9) |
|||
|
|
N = M yC + (m1 + m2 + m3 )g , |
|||
где yC |
|
&& |
определим сначала |
yC (t). |
|
пока неизвестно. Для |
нахождения yC |
||||
&& |
|
|
&& |
|
|
Координата yC центра масс системы определяется по формуле |
|
||||
|
|
M yC = m1 y1 + m2 y2 + m3 y3 . |
(10) |
||
Из рис. Д2 видно, что в произвольный момент времени ординаты грузов равны соответственно y1 = H + Rsin ϕ1 , y2 = H − r cosϕ2 , а y3 = H = OC30 = const .
81
Подставляя эти выражения в формулу (10) и учитывая заданные зависимости ϕ1 и ϕ2 от t, получим
M yC (t) = (m1 + m2 + m3 )H + m1Rsin(πt) − m2r cos(π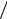 2 − πt
2 − πt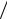 2) или M yC (t) = (m1 + m2 + m3 )H + m1Rsin(πt) − m2r sin(πt
2) или M yC (t) = (m1 + m2 + m3 )H + m1Rsin(πt) − m2r sin(πt 2).
2).
Продифференцировав обе части этого равенства два раза по времени,
найдем M &y&C = −m1Rπ2 sin(πt) + m2r(π2 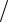 4)sin(πt
4)sin(πt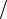 2).
2).
Подставив это значение M &y&C в уравнение (9), определим искомую зависимость N от t.
Ответ: N = 254,8 −1,2π2 [6sin(πt) − sin(πt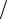 2)], где t – в секундах, N – в
2)], где t – в секундах, N – в
ньютонах.
Задача Д3 (тема: “Теорема об изменении кинетического момента
системы относительно оси”)
Однородная горизонтальная платформа (круглая радиуса R или
прямоугольная со сторонами R |
и 2 R , |
где |
R=1,2 |
м) массой m1 = 24 |
кг |
вращается с угловой скоростью |
ω0 = 10 |
с-1 |
вокруг |
вертикальной оси |
z , |
отстоящей от центра масс C платформы на расстояние OC = b (рис. Д3.0-Д3.9, табл. Д3); размеры для всех прямоугольных платформ показаны на рис. Д3.0а (вид сверху).
В момент времени t0 = 0 по желобу платформы начинает двигаться (под действием внутренних сил) груз D массой m2 = 8 кг по закону s = AD = F (t) ,
где s выражено в метрах, а t – в секундах. Одновременно на платформу начинает действовать пара сил с моментом M (задан в Ньютоно-метрах; при M < 0 его направление противоположно показанному на рисунке).
Определить, пренебрегая массой вала, зависимость ω = f (t), т.е. угловую
скорость платформы, как функцию времени.
На всех рисунках груз D показан в положении, при котором s > 0 (когда s < 0 , груз находится по другую сторону от точки A). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии OC = b от центра C .
Перед выполнением задания прочтите по учебнику тему: «Теорема об изменении кинетического момента системы». Ответьте на вопросы:
8.Вычисление моментов количества движения материальной точки относительно неподвижного центра и неподвижной оси.
9.Определения: кинетический момент механической системы относительно неподвижного центра и неподвижной оси.
10.Сформулируйте теоремы об изменении кинетических моментов механической системы относительно неподвижного центра и неподвижной оси, запишите соответствующие уравнения.
11.Чему равен кинетический момент вращающегося твердого тела относительно оси вращения?
82
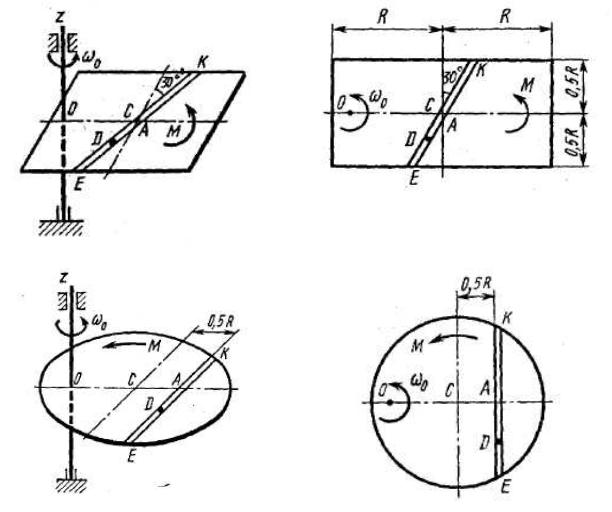
12.Что такое момент инерции твердого тела относительно оси? Что такое радиус инерции?
13.Сформулируйте теорему о моментах инерции относительно параллельных осей.
14.Запишите дифференциальное уравнение вращательного движения твердого тела относительно неподвижной оси.
|
|
|
Таблица Д3 |
|
|
|
|
Номер условия |
b, м |
s = F (t), м |
М, Нм |
0 |
R |
– 0,4 t 2 |
6 |
1 |
R / 2 |
– 0,6 t 2 |
4 t |
2 |
R |
– 0,8 t 2 |
– 6 |
3 |
R / 2 |
10 t |
– 8 t |
4 |
R |
0,4 t 3 |
10 |
5 |
R / 2 |
– 0,5 t |
– 9 t 2 |
6 |
R |
– 0,6 t |
8 |
7 |
R / 2 |
0,8 t |
6 t 2 |
8 |
R |
0,4 t 3 |
– 10 t |
9 |
R / 2 |
0,5 t 2 |
12 t 2 |
Рис. Д3.0 |
Рис. Д3.0а |
Рис. Д3.1 |
Рис. Д3.1а |
83
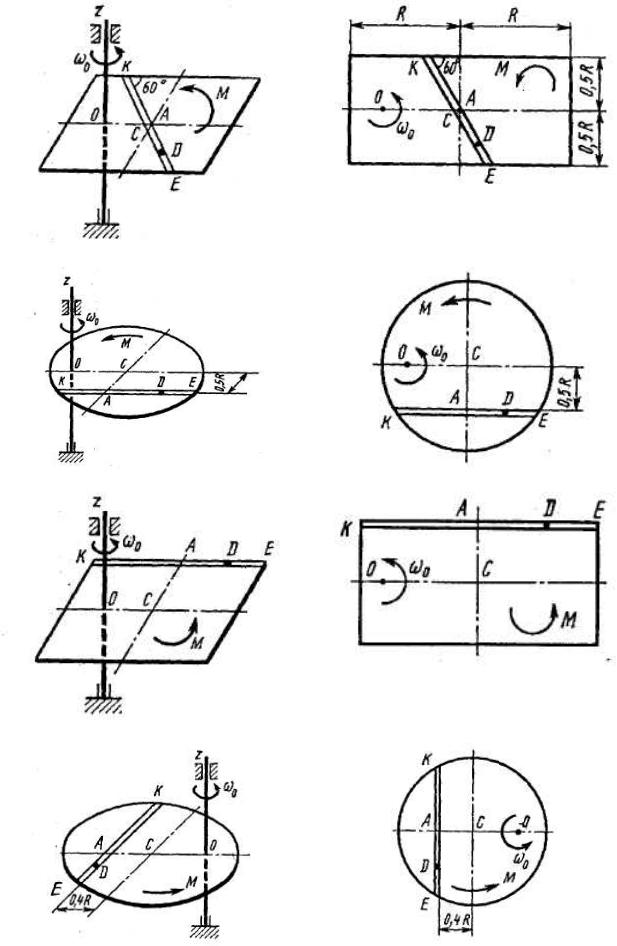
Рис. Д3.2 |
Рис. Д3.2а |
Рис. Д3.3 |
Рис. Д3.3а |
Рис. Д3.4 |
Рис. Д3.4а |
Рис. Д3.5 |
Рис. Д3.5а |
84
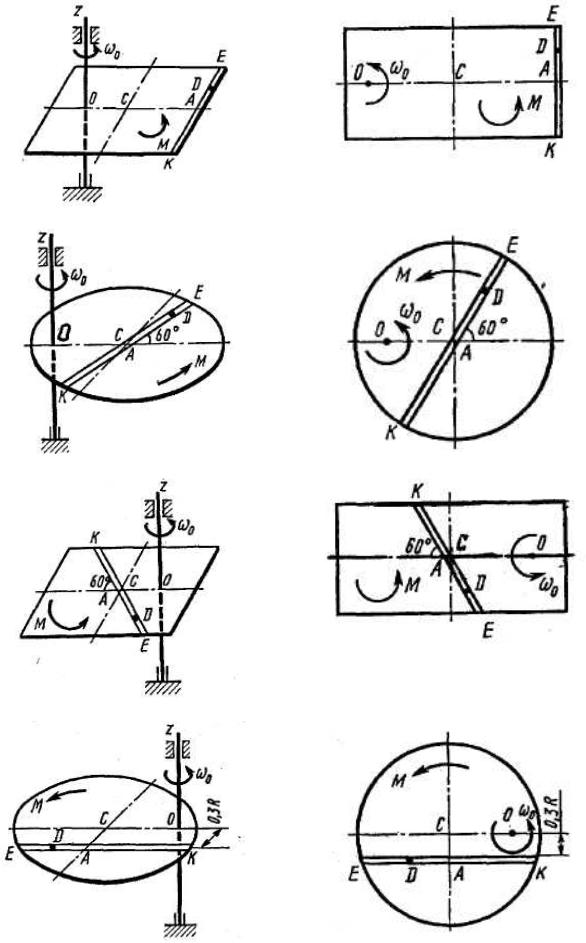
Рис. Д3.6 |
Рис. Д3.6а |
Рис. Д3.7 |
Рис. Д3.7а |
Рис. Д3.8 |
Рис. Д3.8а |
Рис. Д3.9 |
Рис. Д3.9а |
85

Теорема об изменении кинетического момента механической системы
(краткие сведения из теории)
Основные понятия
Количество движения (импульс) точки – это вектор, равный mV , где m – масса точки, V – абсолютная скорость точки.
Момент количества движения точки относительно какой-либо оси z mz (mV ) определяется так же, как момент силы относительно оси z mz (F ) ; в частности, mz (mV ) = 0 если вектор V параллелен z или прямая, на которой
расположен вектор V , пересекает ось z.
Кинетический момент системы K z относительно какой-либо оси z равен
(алгебраической) сумме моментов количеств движения точек относительно этой оси:
|
|
|
|
K z = åmz (mkVk ) . |
|
||
Кинетический момент вращающегося твердого тела |
относительно |
||
(неподвижной) оси вращения z равен |
|
||
K z = J z ω, |
(1) |
||
где ω – угловая скорость тела, |
|
||
J z = åmk hk2 – |
|
||
– момент инерции тела относительно оси z; здесь mk – масса точки тела, hk –
расстояние от этой точки до оси z.
Момент инерции тела зависит от формы тела и положения оси z. Значения J z для однородных тел простой формы (кольцо, стержень, диск,
прямоугольник, цилиндр и т. д.) приводятся в справочниках по механике; значения J z , необходимые для решения данной задачи, приведены ниже в
указаниях к решению.
Если задан радиус инерции ρ тела, то J z = Mρ2 , где M – масса тела. Теорема Гюйгенса (теорема о моментах инерции относительно
параллельных осей): J Az = JCz + Md 2 ; где JCz |
– |
момент |
инерции тела |
относительно оси, проходящей через центр масс, |
J Az |
– момент инерции тела |
|
относительно оси Az, параллельной оси Cz, M – |
масса тела, |
d – расстояние |
|
между осями Az и Cz. |
|
|
|
Теорема об изменении кинетического момента системы относительно неподвижной оси
Формулировка: производная по времени от кинетического момента системы относительно неподвижной оси z равна (алгебраической) сумме моментов внешних сил относительно этой оси; математическая запись:
86

|
dK z |
= åmz ( |
Fke ) . |
|
(2) |
||
|
|
|
|||||
|
dt |
|
|
||||
Частный случай (закон сохранения K z ) |
|
|
|||||
Если внешние силы таковы, что åmz ( |
Fke ) = 0 , |
то K z |
= const , то есть |
||||
K z (t) = K z (0) . |
|
|
|||||
Дифференциальное уравнение вращательного движения твердого тела |
|||||||
Для вращающегося твердого тела, подставляя (1) в |
(2) и |
учитывая, что |
|||||
J z = const , найдем |
|
|
|||||
J z ε = åmz ( |
Fke ) – |
|
|
||||
– дифференциальное уравнение вращательного движения твердого тела; здесь
ε = ω& – угловое ускорение тела.
Указания. Задача ДЗ – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент Kz системы
относительно оси z определяется как алгебраическая сумма кинетического момента платформы и момента количества движения груза. При этом следует учесть, что количество движения груза равно произведению его массы на
абсолютную скорость Vабс , которая складывается из относительной Vотн и
|
|
пер скоростей, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
переносной V |
т.е. Vабс = Vотн +Vпер . Поэтому и количество |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
движения этого груза mV |
абс |
равно mVабс = mVотн + mVпер . Тогда для вычисле- |
|||||||||||||||
ния момента количества движения груза D mz (mVабс ) можно воспользоваться
теоремой |
|
|
|
|
|
|
|
|
|
||||||
Вариньона (статика): mz (mV |
абс ) = mz (mVотн ) + mz (mVпер ); |
эти |
|||||||||||||
моменты |
вычисляются так же, как моменты сил. |
Подробнее ход решения |
|||||||||||||
разъяснен в примере Д3. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
При решении задачи полезно изобразить на вспомогательном чертеже |
|||||||||||||||
вид платформы сверху (с конца оси z ), как это сделано на рис. Д3.0а-Д3.9а. |
|
||||||||||||||
Момент инерции однородной пластины массы m относительно оси Cz , |
|||||||||||||||
перпендикулярной пластине и проходящей через ее центр масс C , равен: |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
= |
m (a2 |
+ a2 ) |
|
|||
для прямоугольной пластины со сторонами a и a |
2 |
J |
Cz |
1 |
2 |
|
; |
||||||||
|
|
|
|||||||||||||
|
1 |
|
|
|
12 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
для круглой пластины радиуса R |
|
|
|
JCz |
= |
m R2 |
. |
|
|
||||||
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
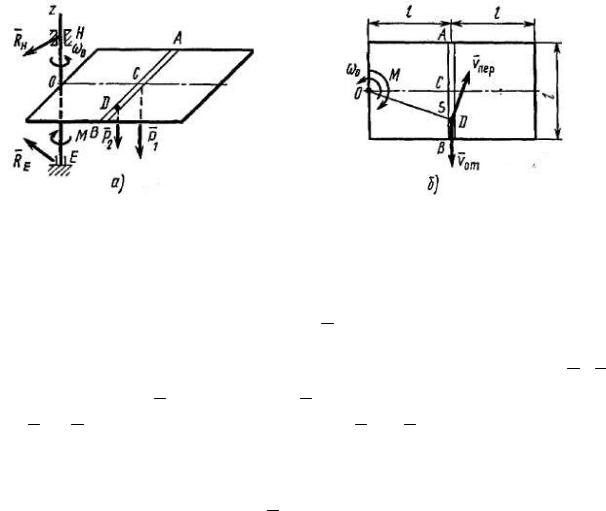
Пример ДЗ. Однородная горизонтальная платформа (прямоугольная со сторонами 2l и l ), имеющая массу m1, жестко скреплена с вертикальным
валом и вращается вместе с ним вокруг оси z с угловой скоростью ω0 (рис. ДЗа). В момент времени t0 = 0 на вал начинает действовать пара сил с вращающим моментом M = −kt (на рис. Д3 отрицательный знак M уже учтен в
показанных противоположных направлениях M и |
ω0 ); одновременно груз |
D |
массой m2 , находящийся в желобе AB в точке |
C , начинает двигаться |
по |
желобу (под действием внутренних сил) по закону s = CD = F (t). |
|
|
Дано: m1 = 16 кг, m2 = 10 кг, l = 0,5м, ω0 = 2 с-1, s = 0,4 t2 (s – в метрах, |
t |
|
– в секундах), k = 6 H ×м/с. |
|
|
Определить: w = f (t) – закон изменения угловой скорости платформы.
Рис. Д3
Решение. Рассмотрим механическую систему, состоящую из платформы и груза D . Для определения угловой скорости ω применим теорему об изменении кинетического момента системы относительно оси z:
dKz |
= åmz ( |
Fke ). |
(1) |
|
|||
dt |
|
||
Изобразим действующие на систему внешние силы: силы тяжести P1, P2 , реакции подпятника RE , подшипника RH и вращающий момент M . Так как силы P1 и P2 параллельны оси z , а реакции RE и RH эту ось пересекают, то
их моменты относительно оси z равны нулю. Тогда, считая для момента положительным направление ω0 (т.е. против хода часовой стрелки), получаем
åmz (Fke ) = M = − kt ,
иуравнение (1) принимает вид:
dKz |
= − kt. |
(2) |
|
dt |
|||
|
|
||
|
88 |
|

Умножая обе части этого уравнения на dt и интегрируя, получим |
|
||||
K |
z |
= − |
k t2 |
+ C . |
(3) |
|
|||||
|
2 |
1 |
|
||
|
|
|
|
||
Для рассматриваемой механической системы |
|
||||
|
Kz = Kzпл + KzD , |
(4) |
|||
где Kzпл и KzD – кинетические моменты относительно оси z платформы и груза D соответственно.
Поскольку платформа вращается вокруг оси z, то ее кинетический момент равен произведению момента инерции относительно оси z на угловую скорость:
|
|
|
|
Kzпл = J z w. |
|
|
|
(5) |
Значение момента инерции платформы относительно оси z найдем по |
||||||||
теореме Гюйгенса: |
|
|
|
|
|
|
|
|
J |
z |
= J |
Cz |
+ m ×(OC)2 = J |
Cz |
+ m l 2 |
, |
(6) |
|
|
1 |
1 |
|
|
|||
где JCz – момент инерции платформы относительно оси Cz, параллельной оси z и проходящей через центр масс платформы C .
Момент инерции JCz относительно оси, проходящей через центр масс платформы перпендикулярно ее плоскости, равен:
J |
Cz |
= m [(2l)2 + l 2 ]/12 = 5m l2 |
/12. |
||
|
1 |
|
1 |
|
|
Тогда |
|
|
|
|
|
J |
z |
= 5 m l 2 |
/12 + m l 2 |
=17m l 2 /12. |
|
|
1 |
1 |
1 |
|
|
Следовательно, |
|
|
|
|
|
|
|
K пл = (17m l2 |
/12) w. |
(7) |
|
|
|
z |
1 |
|
|
Для определения |
|
KzD обратимся к рис. Д3б и рассмотрим движение |
|||
груза D как сложное, |
считая |
его движение по |
платформе относительным |
||
движением, а вращение самой платформы вокруг оси z – переносным
движением. Тогда абсолютная скорость груза |
|
|
|
|
|
|
|
|
|
|
|||||||
|
VD = Vотн + Vпер , |
и по теореме |
|||||||||||||||
Вариньона, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K D = m |
|
|
|
|
) + m |
|
|
|
|
(8) |
|||||||
z |
(m V |
|
z |
(m V ). |
|||||||||||||
z |
2 отн |
|
|
2 пер |
|
||||||||||||
Так как груз D движется по закону s = CD = 0,4t2 , то
υотн = s& = 0,8t .
Изображаем вектор Vотн на рис. Д3б с учетом знака s& (при s& < 0 направление Vотн было бы противоположным).
89

Затем, учитывая направление угловой скорости ω , изображаем вектор переносной скорости Vпер (Vпер ^OD) . Модуль переносной скорости равен
Vпер = w×OD .
Тогда равенство (8) примет вид:
|
|
|
K zD = - m2Vотн ×OC + m2Vпер ×OD = -m2 ×0,8t ×l + m2 w(OD)2 . |
(9) |
||||||
Но на рис. Д3б видно, что |
|
|
|
|||||||
|
|
|
|
|
|
OD2 = l2 + s2 = l2 + 0,16t4 , |
|
|||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K D = - m × 0,8t × l + m w(l2 + 0,16t4 ) . |
(10) |
|||||
|
|
|
|
|
|
z |
2 |
|
2 |
|
Подставляя Kzпл и KzD |
|
из (7) и (10) в равенство (4), получим с учетом данных |
||||||||
задачи: |
|
|
|
|
|
|
|
|
|
|
K |
z |
= |
17 |
m l2 w + m |
|
w(l2 |
+ 0,16t4 ) - m |
|
× 0,8t × l = (8,17 +1,6t4 )w - 4t . |
(11) |
|
|
|
||||||||
|
12 |
1 |
2 |
|
|
2 |
|
|
||
Тогда уравнение (3), где k = 6, принимает вид |
|
|||||||||
|
|
|
|
|
|
|
(8,17 +1,6t4 )w - 4t = -3t2 + C . |
(12) |
||
|
|
|
|
|
|
|
|
|
1 |
|
Постоянную интегрирования определяем из начального условия: при |
t = 0 |
|||||||||
ω = ω0 = 2 с-1, откуда получаем |
|
|
|
|||||||
|
|
|
|
|
|
C |
= (8,17 +1,6t4 )w =16,34 . |
|
||
|
|
|
|
|
|
1 |
|
|
0 |
|
При этом значении C1 из уравнения (12) находим искомую зависимость w от t.
Ответ:
w = 16,34 + 4t - 3t2 , 8,17 +1,6t4
где t – в секундах, w – в с-1.
Задача Д4 (тема: “Теорема об изменении кинетической энергии системы”)
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного
блока) 5 (рис. Д4.0-Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром (диском), массу блока 4 – равномерно распределенной по ободу.
90
