
1. Логарифм ұғымы. Логарифмдік функция
1.1. ЛОГАРИФМ ТҮСІНІГІ ЖӘНЕ ЛОГАРИФМНІҢ НЕГІЗГІ ҚАСИЕТТЕРІ
Логарифм түсінігі
Анықтама. b оң санының а (а>0, a≠1) негізі бойынша логарифмі деп а санының b-ға тең дәреже көрсеткішін айтады.
а
негізі бар b
санының логарифмін
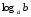 символымен белгілейді.
символымен белгілейді.
Егер
(а>0,
a≠1,
b
>0) болса, онда
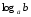 - олb-ны
алу үшін а
санының қандай да бір дәрежесі болады.
- олb-ны
алу үшін а
санының қандай да бір дәрежесі болады.
Сондықтан
 тепе-теңдігілогарифмнің
негізгі тепе-теңдігі
деп аталады. Мысалы,
тепе-теңдігілогарифмнің
негізгі тепе-теңдігі
деп аталады. Мысалы,
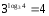 ,
,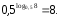
Ондық
логарифмдерді белгілеу үшін арнайы
жазу қолданылған:
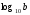 орнына (мұндағыb-кез-келген
оң сан)
орнына (мұндағыb-кез-келген
оң сан)
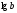 деп
жазады.
деп
жазады.
Логарифмнің қасиеттері.
1.
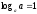 дәлелдеу:
дәлелдеу:
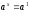
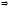
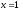
2.
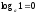 дәлелдеу:
дәлелдеу:
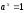
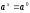
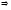
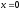
3.
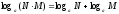
дәлелдеу:
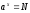
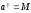
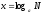
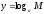


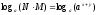
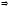
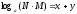
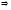
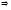

4.
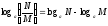
дәлелдеу:
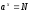

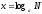
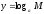
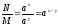
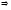
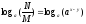
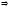
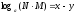
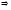
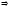
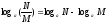
5.

дәлелдеу:
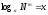
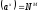
6.
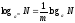
7.

8.
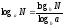
Көбейтудің, бөлудің және дәреженің логарифмдері туралы теоремалар.
1°.
Екі не одан да көп оң сандардың
көбейтіндісінің логарифмі олардың
әрбіреулерінің логарифмдерінің
қосындысына тең, яғни
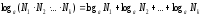 ,
мұндағыа>0,
a≠1,
,
мұндағыа>0,
a≠1,
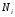 >0.
>0.
2°.Оң сандардың алымының бөліміне қатынасының логарифмі оның бөлінгішінің логарифмінен бөлгішінің логарифмін азайтқанға тең, яғни
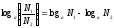 ,
мұндағы а>0,
a≠1,
,
мұндағы а>0,
a≠1,
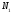 >0,
>0,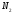 >0.
>0.
3°. Дәреженің логарифмі оның негізінің логарифмінің осы дәреже көрсеткішіне көбейтіндісіне тең, яғни
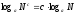 ,
мұндағы
,
мұндағы
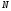 >0,а>0,
a≠1.
>0,а>0,
a≠1.
Ескерту.
Егер
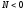 ,
алс-жұп
сан болса, онда
,
алс-жұп
сан болса, онда
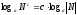 ,формуласы
орындалады, мұндағыа>0,
a≠1.
,формуласы
орындалады, мұндағыа>0,
a≠1.
4°.
b
негізі бар логарифмнен a
негізі
бар логарифмге көшу формуласы
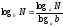 түрінде болады, мұндағы
түрінде болады, мұндағы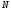 >0,а>0,
a≠1,
b>0,
b≠1.
>0,а>0,
a≠1,
b>0,
b≠1.
5°.
Егер
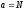 болса, онда формула
болса, онда формула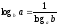 түрінде болады, мұндағыа>0,
a≠1,
b>0,
b≠1.
түрінде болады, мұндағыа>0,
a≠1,
b>0,
b≠1.
6°.
Егер логарифмнің негізін және логарифм
астындағы санды нөлден өзгеше бірдей
дәрежеге келтірсе, онда логарифмнің
мәні өзгереді, яғни
 ,
мұндағы
,
мұндағы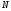 >0,а>0,
a≠1.
>0,а>0,
a≠1.
Логарифмдік функция, оның қасиеті және графигі
1°.Логарифмдік және көрсеткіштік функциялар бір негізге ие болғанда бір-біріне кері функциялар болады.
2°.1(а)
–суретінде
а>0
болғандағы
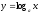 функциясының графигі көрсетілген, ал
1(б) –суретінде
функциясының графигі көрсетілген, ал
1(б) –суретінде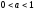 болғандағы
болғандағы функциясы көрсетілген.
функциясы көрсетілген.
y
y
a)
б)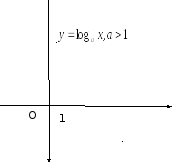

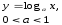
x
x
3°.
а>1
болғандағы
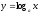 функциясының қасиеті:
функциясының қасиеті:
а)
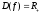 ;
;
б)
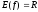 ;
;
в)
функция өспелі;
г)
егер
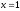 болса, онда
болса, онда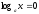 ;
;
д)
егер
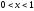 болса, онда
болса, онда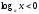 ;
е)
егер
;
е)
егер
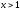 болса, онда
болса, онда ;
;
Логарифмдеу және потенцирлеу
1°. Логарифмдеу – айнымалысы бар өрнектің логарифмі айнымалылардың логарифмдерінің қосындысына немесе айырмасына келтірілетін түрлендіру.
2°.
Логарифмдердің қосындысы
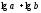 мен қосындының логарифмін
мен қосындының логарифмін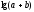 қатаң айыра білу керек. Логарифмдердің
қосындысы көбейтіндінің логарифміне
тең, яғни
қатаң айыра білу керек. Логарифмдердің
қосындысы көбейтіндінің логарифміне
тең, яғни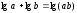 ,
ал қосындының логарифміне
,
ал қосындының логарифміне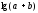 формула
жоқ[4].
формула
жоқ[4].
3°. Потенцирлеу – логарифмдеуге кері түрлендіру.
Логарифмдерді салыстыру.
Егер
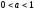 және
және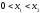 болса, онда
болса, онда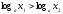 -
теңсіздік таңбасы өзгереді.
-
теңсіздік таңбасы өзгереді.
Егер
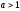 және
және болса, онда
болса, онда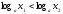 -
теңсіздік таңбасы өзгермейді.
-
теңсіздік таңбасы өзгермейді.
Егер
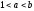 және
және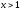 болса, онда
болса, онда
Егер
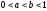 және
және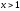 болса, онда
болса, онда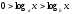
Егер
 және
және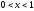 болса, онда
болса, онда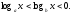
Егер
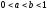 және
және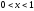 болса, онда
болса, онда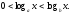
Логарифмдік теңдеулер
Логарифмдік теңдеулерді шешуде көп жағдайда логарифмді көбейтудің, бөлудің, дәреженің, түбірдің қасиеттері қолданады.
Сол қасиеттерді атап өтейік:
1°.
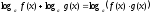
2°.
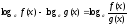
3°.
 егер
егер
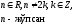
1°-3° формулаларындағы барлық логарифмдер а>0, a≠1 бірдей негізіне ие.
1.
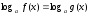 түріндегі
және осы түрге келтірілетін теңдеулерді
шешу.
түріндегі
және осы түрге келтірілетін теңдеулерді
шешу.
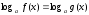 (1)
түріндегі және осы түрге келтірілетін
теңдеулерді келесі әдістермен шешуге
болады:
(1)
түріндегі және осы түрге келтірілетін
теңдеулерді келесі әдістермен шешуге
болады:
1-әдіс.
(1) теңдеуінің салдары болатын
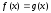 (2)
теңдеуін
(1) теңдеуіне алмастыра отырып, оның
түбірлерін тексеріп, шешу керек. Егер
(1) теңдеуінің өзі кейбір логарифмдік
теңдеудің салдары болса, онда түбірлерді
тексеру (1) теңдеуіне алмастыру арқылы
емес, сол кейбір логарифмдік теңдеуге
алмастыру арқылы тексеріледі.
(2)
теңдеуін
(1) теңдеуіне алмастыра отырып, оның
түбірлерін тексеріп, шешу керек. Егер
(1) теңдеуінің өзі кейбір логарифмдік
теңдеудің салдары болса, онда түбірлерді
тексеру (1) теңдеуіне алмастыру арқылы
емес, сол кейбір логарифмдік теңдеуге
алмастыру арқылы тексеріледі.
2-әдіс.
(2) теңдеуін шешіп, оның түбірлерін не
(1) теңдеуінің анықталу облысы болатын
 (3) теңсіздіктер жүйесіне, не (3) жүйесінің
шешімі болатын теңсіздігіне алмастыра
отырып шешу керек. Егер (1) теңдеуінің
өзі кейбір логарифмдік теңдеудің салдары
болса, онда түбірлерді тексеру (1)
теңдеуінің емес, анықталу облысы
берілетін теңсіздікке алмастыру арқылы
тексеріледі.
(3) теңсіздіктер жүйесіне, не (3) жүйесінің
шешімі болатын теңсіздігіне алмастыра
отырып шешу керек. Егер (1) теңдеуінің
өзі кейбір логарифмдік теңдеудің салдары
болса, онда түбірлерді тексеру (1)
теңдеуінің емес, анықталу облысы
берілетін теңсіздікке алмастыру арқылы
тексеріледі.
3-әдіс.
Бұл әдісте (1) теңдеуінің анықталу облысы
(1) теңдеуін шешу барысында қарастырылады.
Бұл әдісті қолдану арқылы (2) теңдеуінен
және (3) теңсіздігінен құрастырылған
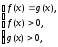 аралас жүйесін шешеміз.
аралас жүйесін шешеміз.
Бұл аралас жүйе (1) теңдеуіне тепе-тең болады. Егер (1) теңдеуінің өзі кейбір логарифмдік теңдеудің салдары болса, онда бұл теңдеуге тепе-тең аралас жүйесіне (2) теңдеуі ғана емес, (1) теңдеуінің емес, берілген теңдеудің анықталу облысы берілетін теңсіздіктері де кіреді.
Логарифмдік
теңдеулерді шешуде үш негізгі әдіс
қолданылады: потенцирлеу әдісі, яғни,
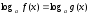 теңдеуінен
салдары болатын
теңдеуінен
салдары болатын
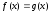 теңдеуіне
көшу; жаңа айнымалыларды енгізу әдісі;
логарифмдеу әдісі, яғни,
теңдеуіне
көшу; жаңа айнымалыларды енгізу әдісі;
логарифмдеу әдісі, яғни,
 теңдеуінен
теңдеуінен
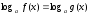 теңдеуіне
көшу.
теңдеуіне
көшу.
2.
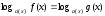 (4)
түріндегі және осы түрге келтірілетін
теңдеулерді шешу
(4)
түріндегі және осы түрге келтірілетін
теңдеулерді шешу
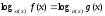 түріндегі
және осы түрге келтірілетін теңдеулерді
шешу (1) теңдеуін шешуде қолданылатын
үш әдістің кез-келгені қолданыла алады.
(1) теңдеуінің анықталу облысы жазылатын
теңсіздіктеріне
түріндегі
және осы түрге келтірілетін теңдеулерді
шешу (1) теңдеуін шешуде қолданылатын
үш әдістің кез-келгені қолданыла алады.
(1) теңдеуінің анықталу облысы жазылатын
теңсіздіктеріне
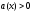 және
және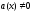 шарттарын қосуды ескеру керек.
шарттарын қосуды ескеру керек.
Сондықтан,
(4) түріндегі теңдеуді екінші не үшінші
әдіспен шешуде (2) теңдеуінің түбірлерінен
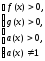 жүйесіне қанағаттандыратын түбірлер
ғана алынады.
жүйесіне қанағаттандыратын түбірлер
ғана алынады.
3. Әр түрлі логарифмдік теңдеулер
1-мысал.
Теңдеуді шеш:
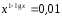 .
.
Шешуі.
Анықталу облысы
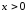 .Бұл
облыста теңдеудің екі жағындағы өрнек
оң мәндер қабылдайды, яғни бұл теңдеулердің
логарифмі болады. екі жағынан да ондық
логарифм аламыз:
.Бұл
облыста теңдеудің екі жағындағы өрнек
оң мәндер қабылдайды, яғни бұл теңдеулердің
логарифмі болады. екі жағынан да ондық
логарифм аламыз:
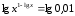 немесе
немесе
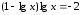 .
Енді
.
Енді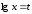 деп алып келесі квадраттық теңдеуді
аламыз:
деп алып келесі квадраттық теңдеуді
аламыз: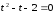 ,
мұндағы
,
мұндағы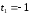 ,
,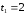 .
Бұдан берілген есеп келесі шешімдер
жиына келді:
.
Бұдан берілген есеп келесі шешімдер
жиына келді: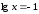 ;
;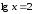 ;
Енді
;
Енді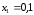 ;
; екенін анықтаймыз.
екенін анықтаймыз.
Тексеру.
табылған
х-тің
екі шешімі де теңдеудің анықталу
облысында жататындықтан
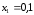 және
және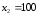 -
теңдеудің түбірлері[2].
-
теңдеудің түбірлері[2].
Логарифмдік теңсіздіктер
1. Айнымалысы логарифмнің астында болатын теңсіздікті логарифмдік теңсіздік деп атайды.
Мысалы,
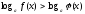 ,
,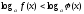 теңсіздіктері логарифмдік теңсіздіктер,
мұндағы
теңсіздіктері логарифмдік теңсіздіктер,
мұндағы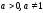 .
.
2.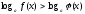 теңсіздігі
теңсіздігі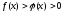 теңсіздігіне тепе-тең болады, сонда тек
сонда, егер
теңсіздігіне тепе-тең болады, сонда тек
сонда, егер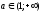 болады және
болады және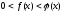 теңсіздігіне тепе-тең болады, егер
теңсіздігіне тепе-тең болады, егер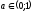 .
.
3. Логарифмдік теңсіздіктерді шешуде жалпы теңсіздіктердің қасиеттерін, логарифмдік функцияның монотондығының қасиеттерін және оның анықталу облысын ескерген жөн.
4.
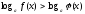 (5) түріндегі логарифмдік теңсіздіктерді
шешу келесі екі теоремаға негізделген,
мұндағы
(5) түріндегі логарифмдік теңсіздіктерді
шешу келесі екі теоремаға негізделген,
мұндағы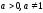 :
:
1-
теорема. Егер
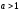 болса, онда (5) теңсіздігі келесі
теңсіздікке тепе-тең болады:
болса, онда (5) теңсіздігі келесі
теңсіздікке тепе-тең болады: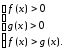 (6)
(6)
2-теорема.
Егер
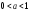 болса, онда (1) теңсіздігі келесі
теңсіздікке тепе-тең болады:
болса, онда (1) теңсіздігі келесі
теңсіздікке тепе-тең болады: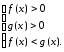 (7)
(7)
Логарифмдік теңсіздіктерді шешудің сызбасы
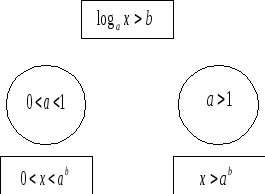
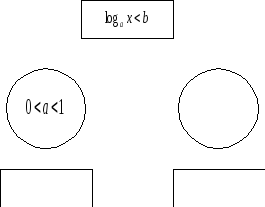
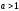
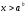
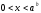
2-мысал.Теңсіздікті
шешіңіз:
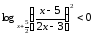 .
.
Шешуі:
Теңсіздікті келесі түрде жазып аламыз:
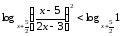
Берілген
логарифмдердің
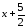 негізіне қарап бұл теңсіздіктерді
келесі теңсіздіктер жүйесіне тепе тең
болады деп айта аламыз:
негізіне қарап бұл теңсіздіктерді
келесі теңсіздіктер жүйесіне тепе тең
болады деп айта аламыз:
1)
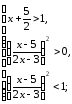 2)
2)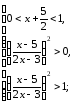
немесе
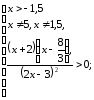
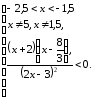
Бұл
жиынның шешімі – (-2;-1,5)
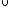 (
(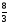 ;5)
;5) (5;
(5; )
осы берілген теңсіздіктің шешімі
болады[2].
)
осы берілген теңсіздіктің шешімі
болады[2].
