Примеры

















































































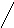
а)

б)

Рис.2.11.1. Гамильтонов граф (а) и его гамильтонов цикл (б)

a



b



c



a



b



c





d



d



e



e

a)

б)

Рис.2.11.2. Полугамильтонов граф (а) и один из его

полугамильтоновых путей (б)

Теоремы

В отличие от эйлеровых графов, неизвестна теорема, которая бы полностью характеризовала гамильтоновы графы. Известны лишь теоремы с достаточными, но не необходимыми условиями.

Теорема Оре

Е

Теорема Дирака

сли deg(v_i) + deg(v_j)  n, n=|V|, для каждой пары несвязных вершин v_i и v_j , тогда граф G будет гамильтоновым.

Если в графе G с n вершинами (n  3) для любой вершины v_i выполняется неравенство

deg(v_i)  n/2 ,

то граф G – гамильтонов.

Пример

4



3



2



1



n=8,

deg(v_i)=3,

неравенство Дирака 3 8/2 =4 не выполняется, следовательно граф негамильтонов.

Однако существует гамильтонов цикл: (1,2,3,4,5,6,7,8,1)



8



7



6



5

Рис.2.11.2. Иллюстрация теоремы Дирака

Класс сложности

Проблема нахождения гамильтонова цикла в графе является частным случаем проблемы путешествующего купца (см. взвешенные графы), когда расстояния между двумя вершинами, соединенных ребром, равно 1 и равно бесконечности в других случаях.

Проблемы нахождения гамильтоновых циклов и гамильтоновых путей являются NP-полными. Однако существуют типы графов, всегда содержащие гамильтонов путь (например, турнир (tournament)).

Алгоритмы

Существует огромная литература по поиску гамильтоновых путей и циклов.

2.12. Понятие “почти все” графы

Определения

Пусть G(n)- множество всех графов на множестве вершинV={1,2,…,n}.Пусть Р - некоторое свойство, которым каждый граф изG(n) может обладать или нет.

Пусть Gp(n)-множество тех графов изG(n), которые обладают свойством Р.

Говорят, что почти все графы обладают свойством Р, если

lim=1

^n-∞

и почти нет графов со свойством Р, если

lim=0

^n-∞

Теоремы

Теорема 1

Почти нет эйлеровых графов.

Теорема 2

Почти все графы связанные.

Теорема 3

Почти все графы гамильтоновы.

Теорема 4

Диаметры почти всех графов равны 2.

2.13. Планарные графы

Определения

П

Теорема

усть задан графG=(V,E). Пусть каждой вершинеviизVсопоставлена точка а_iв некотором евклидовом пространстве, причем а_i≠а_jприi≠j. Пусть каждому ребруe=(v_i,v_j) изEсопоставлена непрерывная криваяL, соединяющая точки а_iиa_j и не проходящая через другие точкиa_k. Тогда если все кривые, сопоставленные ребрам графа, не имеют общих точек, кроме концевых, то это множество точек и кривых называетсягеометрической реализацией графа G.

Каждый конечный граф Gможно реализовать в трехмерном евклидовом пространстве (без пересечения ребер).

Пример

Рис.2.13.1. Укладывание К₃,₃на торе.

Определения

Граф называется планарным, если существует его планарная реализация, то есть имеется геометрическая реализация на плоскости (без пересечения ребер).

Примеры

Планарные графы:

• все деревья;

• все графы циклы;

• все графы колесо;

• некоторые полные графы: K₀,K₁,K₂,K₃,K₄;

• некоторые завершенные

двудольные графы:K_1,n;K_n,2

Не планарные графы:

• K₅;

• K_3,3;

• C₃ C₃

Замечание

Планарность графа часто легче доказать, чем не планарность:

• для того, чтобы доказать планарность графа, достаточно найти его графическое изображение на плоскости без пересечения ребер;

• для того, чтобы доказать не планарность графа, надо доказать, что все возможные графические изображения графа не планарны.

Определение

Планарное представление графа является картой. Карта делит плоскость на области.

Одна из областей всегда неограничена (является частью бесконечной плоскости). Эта область называется внешней.

Пример

R₆– остальная часть бесконечной плоскости

R₄

R₂

R₃

R₁

R₅

Рис.2.13.2. Граф, его карта и области (R₁–R₆)

Теорема Эйлера

Для любого связного графа G, являющегося плоским, справедливо соотношение:

n – m + r = 2,

где n – число вершин, m – число ребер, r – количество областей графа.

Пример





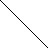
Область 1 - внешняя

Формула Эйлера = n-m+r = 4-6+4 = 2

Грань 3

Область 3

Область 2

Грань 2

Грань 4

Область 4

Рис.2.13.3. Пример планарного графа

Замечание

1. Формула Эйлера позволяет доказать не планарность некоторых графов:

• -полносвязный граф К₅не планарен;

• -двудольный граф К₃,₃не планарен.

2

Теорема

. С графомK_3,3связана следующая старинная задача: Есть три колодца и три дома. Хозяева домов в большой вражде. Можно ли проложить дорожки от каждого дома к каждому колодцу, чтобы они не пересекались?

Планарный граф с числом вершин n3 имеетm3n-6 ребер.

Теорема

Каждый планарный граф G=(V,E) имеет минимальную степень вершин не более пяти, т.е.

(G)  5

Определение

Максимальным планарным графом явялется такой планарный граф, добавление к которому любого нового ребра:

• делает граф планарным;

• или такая операция невозможна, как в случае с полными графами.

Теорема

Максимальный планарный граф с числом вершин nимеетm=3n-6 ребер.

Определение

Подразбиением графа G=(V,E) является любой граф, полученный из G заменой его ребер путем, длиной ко крайней мере один.

Теорема Куратовского

Граф является планарным тогда и только тогда, когда он не содержит в качестве подразбиения ни граф К₅ , ни граф К₃,₃ .

Определение

Операция стягивания в графе G – удаление ребра и отождествление его концевых вершин.

Теорема Вагнера

Граф планарен тогда, когда он не содержит подграфов, стягиваемых к К₅ или К₃,₃ .

Класс сложности

Проблема планарности графа относится к Р-классу.

Имеется несколько алгоритмов, определяющий планарен ли граф за линейное время (основаны, как правило, на теоремах Куратовского и Вагнера).

Алгоритм определения планарности гамильтонова графа (метод цикла)

1. В графе определяется гамильтонов цикл С;

2. Перечисляются оставшиеся ребра графа и делятся на два раздельных множества А и В, где:

• А-множество ребер, которые могут быть нарисованы внутри цикла С без пересечения;

• В -множество ребер, которые могут быть нарисованы вне цикла С без пересечения.

Пример

2

1

8

3

7

4

6

5

Рис.2.13.4.Гамильтонов граф.

Ш

1

аг 1. Находим гамильтонов цикл С:

2

{1,2,3,4,5,6,7,8,1}

8

3

7

4

6

5

Шаг 2.Начинаем перечисление ребер:

{8,2}

{7,2}

{7,5}

{5,2}

{

1

2

4,2}

8

3

4

7

5

6

.

Шаг 3.

{1,3}- пересекается с ребрами А

{8,3}- пересекается с ребрами А

{7,4}- пересекается с ребрами А

1

2

8

3

4

7

Граф планарен

5

6