4. Проблема путешествующего купца

(проблеме коммивояжера)

Определение

Старинная задача звучит так:

Для заданного числа городов, сети дорог и известной стоимости путешествия из одного города в другой найти самый дешевый маршрут однократного посещения каждого города с обязательным возвратом в город-начало путешествия.

Эквивалентная формулировка проблемы коммивояжера в теории графов (орграфов):

Во взвешенном графе (орграфе) найти гамильтонов цикл наименьшего веса.

Класс сложности

Проблема коммивояжера относится к классу NP-тяжелых.

Точные алгоритмы

Известны точные алгоритмы решения проблемы коммивояжера:

• Разные алгоритмы ветвей и границ, применяемые к расчету проблемы коммивояжера с 40-60 вершинами;

• Специальные улучшения техники линейного программирования доводят число вершин до 120-300.

В 2001 году было найдено точное решение проблемы коммивояжера для 15112 немецких городов для одной из задач специальной библиотеки TSPLIB. Решение получено по алгоритму, использующему специальный вариант линейного программирования. Решение проводилось сетью из 100 процессоров. Общее время вычислений эквивалентно 22,6 годам для одного процессораAlpha500 мГц.

Эвристические алгоритмы

Известны различные эвристические алгоритмы решения проблемы коммивояжера, которые «быстро» находят «хорошие» решения с «высокой» точностью. Современные методы могут решить проблемы чрезвычайно большой размерности (миллионы вершин) за приемлемое время; решения отличаются, вероятно, на 2-3% от оптимального решения.

Проблема коммивояжера является пробным камнем, «оселком» для многих общих эвристических алгоритмов.

Особенно интересны алгоритмы, «подсмотренные» у природы:

• Генетические алгоритмы (geneticalgorithms);

• Эволюционное программирование (evolutionprogramming);

• Нейро-сетевые вычисления (neuralnetworkcomputing);

• ДНК-вычисления (DNA-computing);

• Клеточные автоматы (cellblarautomata);

• Муравьиные алгоритмы (antcolonyalgorithms).

Все достаточно точные эвристические алгоритмы для задач большой размерности очень сложны и могут быть реализованы только на компьютерах.

Простой графический алгоритм

Этот эвристический алгоритм находит верхнюю и нижнюю границу веса гамильтонова цикла во взвешенном полносвязном графе. Очевидно, что чем ближе будут верхняя и нижняя граница, тем точнее будет решение.

Алгоритм нахождения верхней границы проблемы путешествующего купца:

1. Начать с конечного множества вершин числом 3 и более, соединенных попарно взвешенными рёбрами меньшего веса.

2. Выбрать любую вершину и найти другую вершину, соединенную с выбранной вершиной ребром наименьшего веса.

3. Найти вершину, которая связана с общими вершинами, идентифицированными на шаге (2), ребром с наименьшим весом. Нарисовать эти три вершины и три ребра, их соединяющего, в виде цикла.

4. Найти вершину вне цикла, которая соединена с любой вершиной цикла ребром наименьшего веса. Зарисовать его вместе с вершиной. Обозначить эту новую вершину v_n, а вершину цикла, к которой через ребро подсоединенаv_n, черезv_k. Кроме того, обозначитьv_k-1вершину, предшествующуюv_k, а черезv_k+1– вершину, последующую после вершиныv_k.

Если для весов ребер выполняется условие:

W(v_k-1,v_n) -W(v_k-1,v_k)W(v_n,v_k+1) -W(v_k,v_k+1),

то в существующем цикле заменить ребро {v_k-1,v_k} на два ребра {v_k-1,v_n} и{v_n,v_k} с вершинойv_nмежду ними.

Если вышеуказанное условие не выполняется, то в существующем цикле заменяем ребро {v_k,v_k+1} на два ребра {v_k,v_n} и{v_n,v_k+1} с вершинойv_nмежду ними.

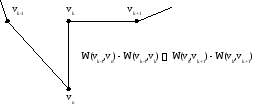
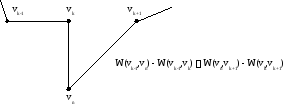
5. Повторить шаг 4 до тех пор, пока не образуется цикл, затем стоп. Полученный цикл является верхней границей решения проблемы путешествующего купца.

Пример

Применим данный алгоритм к полносвязному графу:

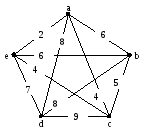
7

1. Начальная вершина – а. Ребро наименьшего веса, соединяющее а с другими вершинами – {a,e}.

2. Ребро наименьшего веса, соединяющее вершину а еще с одной вершиной – ребро {a,c}.

3. Формируем цикл

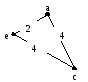
4. Ребро наименьшего веса вне цикла, инцидентное к одной из вершин (a,c,e) – ребро {b,c}.

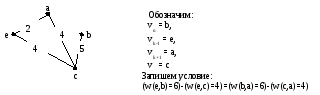
5. Вставляем ребра {c,b} и {a,b} с вершинойbмежду вершинамиaиc, а ребро {a,c}убираем:

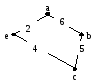
6. Ребро наименьшего веса вне цикла, инцидентное к одной из вершин {a,b,c,e} – ребро {e,d}.

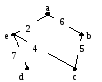
Обозначим:

v_n=d,

v_k-1 = a,

v_k+1 = e,

v_k=c

Запишем условие:

(w(a,d)=8)-(w(a,e)=2)< (w(d,c)=9)-(w(e,c)=4)

7. Вставляем ребра {e,d}и {d,c} между вершинамиeиc, а ребро {c,t}убираем: