2.9.2. Независимое множество вершин

Определения

Независимое множество вершинSесть такое подмножество вершин графаG, что любые две вершины в нем не смежны (никакая пара вершин не соединена ребром).

Среди всех возможных независимых множеств S_iвыделяют наибольшее –максимальное независимое множество вершин.

Пример

Независимые множества вершин

S₁={1,3}S₂={4,6}

S₃={1,4} S₄={3,6}

S₅={1,3,7} S₆={2,7,8}

S₇={2,4,8} S₈={2,5,7,8}

4



3



2



1





6



8



7



5

Максимальное независимое множество вершин

S₈ ={2,5,7,8}

Рис.2.9.2. Независимые множества вершин

Меры

• (G) –число независимости, определяемое числом вершин максимального независимого множества вершин.

Класс сложности

Проблема нахождения независимого множества вершин является NP-полной, а проблема нахождения максимального независимого множества вершин –NP-тяжелой.

Точные решения

Как и в случае проблемы нахождения максимальной клики существуют точные алгоритмы решения, однако они имеют экспоненциальную сложность. Точные решения удается получить для графов с числом вершин менее 500.

Эвристические алгоритмы

Относятся к тем же группам, что и для проблемы нахождения максимальной клики.

Жадный алгоритм

Введем следующее обозначение:

S_i– независимое множество вершин графаG=(V,E).

1. Начальное условие S_i:=0;

2. Если граф не пустой, то случайны образом выбираем вершину v_iс наименьшей степенью;

3. S_i:= S_i  v_i ;

4. Удалить вершину v_iи все инцидентные к ней вершины. Перейти к п.2.

Пример

4



3



2



1



Начальное условие:

S_i:=0



6



8



7



5

Шаг 1. Определяем степени вершин:deg₁=3;deg₂=3;deg₃=3;deg₄=3;deg₅=3;deg₆=5;deg₇=2;deg₈=2.

Имеется две вершины (7 и8) с одинаковой минимальной степенью. Выбираем вершину 8.

S_i:={8}

У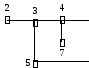даляем вершину 8 и все инцидентные ей вершины (вершины 1 и 6). Получаем подграф

Шаг 2.Определяем степени вершин подграфа, полученного на предыдущем шаге:deg₂=1;deg₃=3;deg₄=3;deg₅=2;deg₇=1.

Имеется две вершины минимальной степени – вершины 2 и 7. Выбираем вершину 2.

S_i:={2,8}

Удаляем вершину 2 и инцидентную ей вершину 3. Получаем подграф

4





7

5 

Шаг 3. Определяем степени вершин подграфа, полученного на предыдущем шаге:deg₄=3;deg₅=2;deg₇=1.

Вершина 7 имеет наименьшую степень.

S_i:={2,7,8}

Удаляем вершину 7 и инцидентную ей вершину 4. Получаем подграф, состоящий из одной вершины 5.

S_i:={2,5,7,8}

Граф пустой, алгоритм стоп.

Полученное множество независимых вершин совпало с максимальным (см.рис.2.9.2), однако это будет не во всех случаях, т.к. алгоритм – жадный.

2 Определения .9.3. Паросочетание графа

Паросочетанием MграфаG=(V,E) является такое подмножество реберE, что никакие два ребра в М не инцидентны любой вершинеvV(иными словами, в М нет двух ребер, имеющих общую вершину).

Вершина vVбудетМ-покрытой, если она инцидентна ребру в М, в противном случае вершина будетМ-непокрытой.

Паросочетание М граф Gбудетсовершенным, если все вершины графа будут М-покрыты.

Среди всех возможных паросочетаний графа выделяют два особых вида:

• максимальное (maximal) паросочетаное- паросчетание М в граф, не содержащееся ни в одном другом паросочетании;

• наибольшее сочетание- паросочетание наибольшего размера среди всех паросочетаний графаG.

Очевидно:

1. в графе могут быть несколько паросочетаний одного наибольшего размера;

2. максимальное паросочетание наибольшее паросочетание.

Меры

• (G) –число паросочетаний, определяемое числом ребер наибольшего паросочетания графа.

• def(G) –дефецит графа- задаваемое числом М-непокрытых вершин графа (если паросочетание является совершенным, тоdef(G)=0).

Класс сложности

Нахождение паросочетания графа относится к NP-полному классу, а проблема определения наибольшего паросочетания –NP-тяжелая.

Точные решения

Точное решение проблемы нахождения наибольшего паросочетания известно (например, используется метод целочисленного линейного программирования), однако время решения проблемы растет экспоненциально с ростом размерности графа.

Алгоритмы для частных типов графов

Наиболее разработанное направление – паросочетания для двудольных графов.

Ниже рассматриваются два подхода:

• сведение к задаче определения максимального потокав сети;

• метод, основанный на поиске дополняющих путей в графе.

Метод максимального пути

Известно приведение проблемы нахождения числа паросочетаний двудольного графа к проблеме нахождения максимального потока в сети, а последняя проблема решается в полиномиальное время.

Это приведение достаточно простое. Для заданного двудольного графа G=(V,E) с двумя подмножествами вершинLиR,V=LR, строится сетьG`=(V`,E`):

1. к графу G=(V,E) добавляется две новые вершины стока и истокаsиt, т.е.V`=V{s,t}.

2. дуги (направленные линии) графа G` задаются следующим образом:E`={{s,u}:L}{{u,v}E:uL,vR}{{v,t}:vR}.

3. Всем дугам, инцидентным sиt, присваивается единичная емкость, а для всех остальных дуг емкость принимается равной бесконечности.

Пример

L

R

●

●

●

●

●

L

R

s

t

емк.=∞

●

●

●

●

●

емк.=1

емк.=1

Рис.2.9.3. Приведение двудольного графа сети

Теорема

Значение наибольшего s-t потока в G` равно числу наибольшего паросочетания в G.

Алгоритм

Наибольший s-tпоток можно найти с помощью алгоритма Форда-Фалкерсона.

Дополняющие пути

Путь P=v₀,v₁,v₂, …,v_kв графеGявляетсяМ-чередующимся, если он содержит поочередно ребра из паросочетания М и ребра вне его (вE/М).

Пусть P=v₀,v₁,v₂, …,v_kбудет простым М-чередующимся путем. Р будетМ-дополняющим путем, еслиv₀иv_kне являются вершинами в паросочетании (они являютсяМ-свободными).

Пример

v_k-1

М-свободная вершина

v₀

v₁

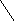
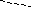
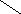
v_k

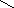
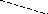
М-свободная вершина

Рис.2.9.4. М-дополняющий путь

Теорема существования

М является наибольшим паросочетанием тогда и только тогда, когда по отношениюк М в графе нет М-дополняющих путей.

Алгоритмы

Эта теорема лежит в основании почти всех известных алгоритмов определения наибольшего паросочетания в произвольном графе. Основная идея этих алгоритмов:

• начав с заданного или нулевого паросочетания, попытаться найти М-дополняющий путь по отношению к данному паросочетанию.

• Использовать эти пути для увеличения паросочетания до тех пор, пока имееются М-дополняющие пути.

Заметим, что число графа с общем случае растет экспоненциально с ростом размера графа. Поэтому потребовались эффективные алгоритмы поиска дополняющих путей.

Для двудольных графов одним из самых эффективных и популярных алгоритмов поиска наибольшего паросочетания является алгоритм Хопкрофта-Карпа (Hopcroft-Karp), исполняемый за О(n⁴) (n– число вершин графа).

Пример

12

 11

12

 11

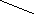
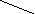
1

 6

1

 6

2

 7

2

 7

3

 8

3

 8

4

 9

4

 9

5

 10

5

 10

Наибольшее паросочетание

{{1,11},{3,10},{4,8}, {5,6}}

Рис.2.9.5. Наибольшее паросочетание, найденное алгоритмом Хоплкофта-Карпа

2.9.4. Вершинное покрытие

Определения

Вершинным покрытием S графа G=(V,E) является подмножеством вершин V, которое инцидентно ко всем ребрам негорафа, т.е. для каждого ребра {u,v}E для uS или vS.

Минимальным вершинным покрытием графаG=(V,E) называется вершинное покрытие минимальной мощностиS`.

Пример

v₂



v₁



Вершинное покрытие

и минимальное вершинное покрытие

S`={v₁, v₄}



v₃



v₄

Рис.2.9.4. Вершинное покрытие

Меры

• (G) –число вершинного покрытияграфа. Является числом вершин минимального вершинного покрытия этого графа.

Класс сложности

Нахождение вершинного покрытия относится к NP-полному классу, а проблема определения минимального вершинного покрытия –NP-полная.

Точное решение

Известны точные решения проблемы минимального вершинного покрытия методом целочисленного программирования или методом ветвей и границ, при этом время расчета растет экспоненциально с увеличением размера графа.

Жадный алгоритм

И

Алгоритм G1

меется большое число жадных алгоритмов для вычисления «приблизительно» минимального вершинного покрытия. Среди них есть два алгоритма, дающих наилучшее приближение к оптимуму.

1. Начальное значение множества вершинного покрытия S:=0;

2. Выбрать любое ребро {u,v};

3. S:=S  {u,v};

4. Удалить вершины uиv, а также все инцидентные к ним ребра и все изолированные вершины.

5. Повторить 2 до тех пор, пока в графе есть ребра.

С

Пример

ложность этого алгоритма –O(n+m), гдеn–число вершин иm– число ребер графа.

e



c



b



Начальное значение

S:=0



a



d



f



g

Шаг 1.Выбираем ребро {e,d};

S:={e,d};

c



b



Удаляем вершиныeиdи все инцидентные к ним ребра и изолированные вершины. Получаем подграф



a

Шаг 2.Выбираем ребро {b,c};

S:={b,c,d,e};

Удаляем все инцидентные ребра и изолированные вершины. Подграф пуст – алгоритм стоп.

Полученное вершинное покрытие неминимально. Минимальным покрытием будет S`={b,d,e}.

Алгоритм G1

1. Вычислить максимальное или даже наибольшее паросочетание М графа G.

2. Взять вершины максимального или наибольшего паросочетания в качестве вершинного покрытия графа G.

Замечание

Аппроксимационное отношение алгоритмов G₁иG₂равно 2.

2.9.5. Реберное покрытие

Определения

Реберным покрытиемназывается подмножество реберU` графаG=(V,E),U`E, такое, что всякая вершина графаGинцидентна ребру изU`.

Минимальное реберное покрытие- минимальное среди всех возможных подмножеств реберных покрытий.

Пример

Рис.2.9.7. Реберное покрытие

Меры

• (G) –число реберного покрытия.Равно размеру |U`| минимального реберного покрытия.

Класс сложности

Проблема нахождения реберного покрытия относится к NP-полным, а вычисление числа реберного покрытия – кNP-тяжелым.

2.9.6. Теоремы о подструктурах графа

Теорема 1 (Идентичности Галлаи-GallaiIdtntities)

Пусть для любого графа G=(V,E) будут

n=|V|,

(G) – число независимости,

(G) – число реберного покрытия,

(G)– число вершинного покрытия,

(G) – число паросочетания,

тогда

• (G) +(G) =n

• (G) +(G) =n, если графGне имеет изолированных вершин.

Теорема 2

Справедливы следующие утверждения:

1. Минимальное реберное покрытие будет минимальным тогда и только тогда, когда оно содержит наибольшее паросочетание.

2. Максимальное паросочетание является наименьшим тогда и только тогда, когда оно содержится в минимальном реберном покрытии.

Теорема 3

Для любого графа G=(V,E) справедливо следующее неравенство

(G)  (G)  2(G).

Теорема 3 (Konig`s Minimax Theorem)

Если G=(V,E) является двудольным графом, то

(G)(G).

7. Доминирующее множество вершин

Определения

Доминирующим множеством (вершин) графаG=(V,E) является подмножествоV’Vтакое, что любая вершина, не находящаяся вV', соединяется по крайней мере одним ребром в вершинами изV’.

Меры

γ(G) –доминантное числографа .Является числом вершин самого меньшего доминирующего множества графа.

Класс сложности

Проблема нахождения наименьшего доминирующего множества относится к NP-полным, а нахождение доминирующего числа –NP-тяжелая задача.

Замечания

Доминирующие множества тесно связаны с независимыми множествами: максимальное независимое множество в графе необходимо является доминирующим множеством. Однако, доминирующее множество может и не быть независимым.

Если S– связное доминирующее множество, то можно сформировать каркасное дерево графаG, в которомSформирует множество вершин дерева, не принадлежащим листьям (степени 1). ЕслиT– каркасное дерево графа с тремя и более вершинами, то не листовые вершины дереваTформируют связное доминирующее множество. Таким образом, нахождение минимального связного доминирующего множества эквивалентно нахождению каркасного дерева с максимально возможным числом листьев.