
шпорки к экзамену за 2й семестр.(Новоселов,Ершов)
.doc
Система векторов a1, a2,…am называется линейно зависимой, если хотя бы один из е векторов может быть представлен в виде линейной комбинации остальных. Система называется линейно независимой, если ни один из ее векторов не может быть представлен в виде линейной комбинации остальных векторов. Теорема. Для того, чтобы система векторов была линейно зависимой, необходимо и достаточно, чтобы существовал такой набор чисел μ1a1 + μ2a2+ …+ μmam=0 Необходимость. Пусть система линейно зависима. Тогда какой-либо вектор, например a1,можно представить в виде линейной комбинации остальных: a1=λ2a2+ λ3a3+…+λmam Отсюда
следует,
что
– Достаточность. Пусть существует набор чисел μ1, μ2,…, μm, в котором, например μ1ǂ 0 и для которого выполняется равенство. Тогда
Т.к. вектор a1 представлен в виде комбинации остальных, что означает линейную зависимость системы векторов. Из
доказательства теоремы следует, что
система линейно независима тогда и
только тогда, когда равенство – |
2.В каком случае вектор b можно назвать линейной комбинацией векторов a1 … an ? Вектором называется упорядоченный набор чисел. Числа в векторе с учетом их расположения по номеру в наборе называются компонентами вектора. Число компонент вектора называется его размерностью.
В-р
8) Матрица А=ai,j, i,j=1,2,3. Разложите определитель матрицы А по элементам второго столбца?
a11 a12 a13 А= a21 a22 a23 a31 a32 a33
1 2 3 4 5 6 = -2* 4 6 + 5*1 3 – 8* 1 3= 7 8 9 7 9 7 9 4 6 |
4.Дайте определение матрицы, обратной квадратной матрице А. Какое условие является необходимым и достаточным условием существования обратной матрицы? Пусть задана кв. матрица А.Если сущ-т матрица В, такая что А*В=Е,то гов что матрица В явл обратной по отношению к мат А: В=А-1, А*А-1=Е. Свойства: 1)Обратная и исходная матрицы перестановочны и матрица,обратная обратной, совпадает с исходной: А*А-1=А-1*А=Е. 2)Единственность матрицы: если для данной матрицы обратная мат сущ-т,то она только одна. Как выяснить явл ли кв. матрица обратной? Пусть исход матрица А имеет вид: а11 а12 а13 А= а21 а22 а23 а31 а32 а33 Предпол что имеется какая-то мат В, В=(хij)=А-1,кот явл обратной по отношению к исходной мат-це А. Тогда должно выполняться: а11 а12 .. а1n x11 x12 .. x1n 10….0 а21 а22 .. а2n * x21 x22 .. x2n = 010...0 …………… ………….. ……. а31 а32 .. а3n xm1 xm2 .. xmn 000001 Это матричное ур-е можно переписать в виде системы n2 линейных ур-й с n2 неизвестными. 3)Квадратная матрица обратима тогда и только тогда, когда она является невырожденной.
|
||||||||||||||||||||
|
5.СЛАУ решается методом Жордана- Гаусса. Каким образом в процессе решения убедиться в том, что СЛАУ: 1)не имеет решения?2)имеет уравнение, являющееся линейной комбинацией каких-либо других уравнений системы?Суть метода состоит в том, что за счёт элементарных преобразований, за конечное число шагов система приводится к так называемому, предпочитаемому или каноническому виду, кот легко исслед-ся и решается. Выбирается разрешающее ур-е, в кот выбирается неизвестная, коэф-т при кот отличен от нуля (разреш-ая неизвестная), а коэф-т при ней назыв разрешающий коэф-т. Путём элем-х преобразований разреш-ая неизвестная искл-ся из всех урав-й системы кроме разрешающей. Берётся след ур-е и след разреш-ая перем-ая отличная от первой, далее путём элем-х преобр-й она искл-ся из всех ур-й системы кроме разрешающей и т.д. Пример: а11х1+а12х2+а1nхn=b1 – разреш урав-е а110 аm1х1-разреш перем-ая нужно искл х1 из всех ур-й кроме разрешающего. Нужно 1-е ур-е умножить на (-а21/а11)= -а21х1- а12*а21/а11*х2 -…- а21*а1n/а11*хn=-b1*а21/а11 + 2 ур-е системы В рез-те преобр-й возможны след.случаи: 1) в процессе реш-я появл равенства 0*х1+0-х2+…+0-хn=bi вi0 при появл такого равенства пишем что сис-ма несовместна. 2) левая и правая части i ур-я обращ-ся в 0, т.е.0=0 данное ур-е явл линейной комбинацией ур-й вход-х в эту систему, в этом случае это ур-е исключается из всей системы 3) После того как будут получены решения системы, либо будет доказана её несовместность, система будет приведена к следующему виду: х1 + q1,m+1*xm+1 + … + q1n*хn=h1 х2 + q2,m+1*xm+1 + … + q2n*хn=h2 . . . . . . . . . . . . . . . хm + qm,m+1*xm+1 + … + qmn*хn=hm В этом случае говорят, что СЛАУ приведена к предпочитаемому или каноническому виду. |
7)дайте определения:
В качестве разрешающей неизвестной можно принять любую неизвестную, при которой есть хоть один положительный коэффициент, а затем в качестве разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему среди отношений свободных членов уравнений к соответствующим положительным коэффициентам при выбранной неизвестной в этих уравнениях. Неизвестные типа X1,X2, …, Xm называют базисными , неизвестные Xm+1, X m+2, Xn – свободные. Так как значения свободных неизвестных можно найти бесконечно много решений системы, называемых ее частными решениями, т.е. в этом случае система является совместной и неопределенной. Выражения базисных неизвестных через свободные вида
X1=h1-g1,m+1 - …- g1nxn ,
Xm = gm,m+1xm+1 - … - gmnxn
естественно назвать общим решением СЛАУ. Среди частных решений системы выделяются базисное , отвечающее нулевым значениям свободных неизвестных :
X1 = h1, x2 = h2, …, xm = hm, xm+1 = 0, …,Xn = 0 |
9) Дайте определение ранга матрицы размером m*n. Определите ранг матрицы (матрица задана). Рангом системы n-мерных в-ров называется максимальное число линейно независимых в-ров этой системы. ранг системы единичных в-ров равен n. Ранг системы в-ров не изменяется, если она подвергается элементарным преобразованиям:
У матрицы размером mxn можно рассматривать строки как n-мерные в-ры, а столбцы как m-мерные в-ры. Ранг системы строк – строчный ранг. Ранг системы столбцов – столбцовый ранг. Таким образом, в прямоугольной матрице они всегда равны. Ранг матрицы – максимальное число линейно независимых рядов.
|
||||||||||||||||||||
|
6)По каким правилам при нахождении неотрицательных решений СЛАУ выбирается разрешающая неизвестная и разрешающее уравнение? Решение
( Если правые части всех уравнений полученных систем окажутся неотрицательными, то соответствующие базисные решения также будут неотрицательными. Следовательно, чтобы получить неотрицательные базисные решения СЛАУ, надо научиться вести процесс исключения неизвестных так, чтобы свободные члены всех уравнений на всех этапах этого процесса оставались неотрицательными. Для этого следует руководствоваться следующими правилами: 1)Если в СЛАУ имеются отрицательные свободные члены, то все такие уравнения необходимо умножить на (-1); 2) В качестве разрешающей неизвестной можно принять любую неизвестную, при которой есть хоть один положительный коэффициент, а затем в качестве разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему среди отношений свободных членов уравнений к соответствующим положительным коэффициентам при выбранной неизвестной в этих уравнениях. Может случиться, что указанное минимальное отношение достигается при нескольких значениях индекса. Тогда любое из соответствующих им уравнений можно принять за разрешающее. Принято говорить в этом случае, что рассматриваемая СЛАУ является вырожденной. СЛАУ не будет иметь ни одного неотрицательного решения, если в процессе симплексных преобразований в ней появится уравнение, в котором свободный член строго положителен, а среди коэффициентов при неизвестных нет ни одного положительного. Преобразования системы в соответствии с этими правилами называются симплекс-преобразованиями системы. |
10) Дайте определения:
Решением СЛАУ называется такая система чисел к1,к2,…кn, которые при подстановке обращает каждое из уравнений системы в верное тождество. В этом случае, когда система имеет решение, она называется совместной, в противном случае противоречивой или несовместной. Совместная система называется определенной или неопределенной в зависимости от того, имеет ли она одно или несколько решений. Две СЛАУ с одинаковым числом неизвестных называются эквивалентными или равносильными, если они имеют одни и те же решения, либо вообще не имеет решений. При этом число уравнений в равносильных системах может быть различным. Те преобразования, которые переводят СЛАУ в эквивалентную ей систему
|
12)Единичная матрица: определение, формулы для элементов. Матрица – это прямоугольная таблица чисел, содержащая m строк и n столбцов. a11 а12 …а1n А= a21 а22 …а2n или кратко А=(aij) ………….. am1 аm2 …аmn Если т=п, то матрица называется квадратной матрицей n-го порядка. Кв. матрица наз треугольной, если все ее элементы, стоящие над или под главной диагональю, равны нулю. Кв. матрица называется диагональной, если все ее эл-ты, стоящие на главной диагонали, отличны от нуля, а остальные равны нулю. Диагональная матрица наз единичной, если у нее по главной диагонали стоят 1. Единичную матрицу принято обозначать буквой Е:
|
||||||||||||||||||||
|
11)Действия над матрицами: сумма, произведение, транспорирование. Свойства и формулы для расчета элементов. Матрицей размера mxn наз таблица чисел, кот расположена в m-строках и n-столбцах a11 а12 …а1n А= a21 а22 …а2n или кратко А=(aij) ………….. am1 аm2 …аmn Если т= п, то матрица называется квадратной матрицей n-го порядка. Кв. матрица наз треугольной, если все ее элементы, стоящие над или под главной диагональю, равны нулю. Кв. матрица называется диагональной, если все ее эл-ты, стоящие на главной диагонали, отличны от нуля, а остальные равны нулю. Диагональная матрица наз единичной, если аii=1, i=1,...,п. Транспонированной матрицей наз матрица, строки кот.заменены столбцами. Единичную матрицу принято обозначать буквой Е:
.
С 2)(АВ)' = В'А' ; 3) (А + В)' = А' + В'. Произведением матрицы А размера т х п на матрицу В размера n х k наз матрица С размера т х k, эл-ты кот сij равны скалярному произведению i-й строки матрицы А на j-й столбец матрицы В, т.е роизведение матриц обозначается С = АВ. Скалярное произведение векторов а и b можно представить как произведение вектора-строки (матрицы-строки) а на вектор-столбец (матрицу-столбец) b': (a, b) = ab'.Для операции произведения матриц справедливы следующие свойства: 1)A(BС) = (АВ)С; 2)(А+В)С=АС+ВС; 3)A(B+С)=AB+AC; 4) λАВ) = (λА)В. 4) λАВ) = (λА)В. К
a11 a12 /A/ = a21 a22 = a11A11 + a12A12=a11a22-a12a21
|
13)Обратная матрица: определение, свойства, условие существования. Пусть задана квадратная матрица А. Если существует матрица В, такая что А*В=Е, то говорят что матрица В является обратной по отношению к матрице А: В=А-1, А*А-1=Е. Свойства: 1)Обратная и исходная матрицы перестановочны и матрица, обратная обратной, совпадает с исходной: А*А-1=А-1*А=Е. 2)Единственность матрицы: если для данной матрицы обратная мат сущ-т,то она только одна. Только квадратная матрица может иметь обратную. Для нахождения обратной матрицы можно использовать следующий алгоритм:
|
14) Постановка линейной производственной задачи, смысл переменных, векторов и матриц, допустимый и оптимальный план, математическая модель. Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему линейных алгебраических уравнений или неравенств и среди всех неотрицательных решений найти то решение, при котором линейная однородная функция принимает наибольшее или наименьшее значение. Изучение методов исследования и решения математических задач указанного типа составляет содержание раздела математики, кот. принято называть линейным программированием. Предположим,
что предприятие выпускает n видов
продукции при использовании m видов
ресурсов. Известны: технологическая
матрица расходов i-го вида ресурса на
единицу j-го вида продукции – А=(аij),
где i=
Известны
прибыль, полученная предприятием от
производства и реализации продукции
j-го вида. Требуется составить план
производства продукции: x
= (x1,
x2,
x3,...xn),
при котором предприятие получит
наибольшую прибыль. Суммарная прибыль
предприятия
Любое неотрицательное значение системы называют допустимым, а допустимое решение, при котором целевая ф-я принимает наименьшее значение – оптимальным решением задачи ЛП. Ограничения по ресурсам записываются в виде: а11x1 + a12x2 + … a1nxn ≤ b1 а21x1 + a22x2 + … a2nxn ≤ b2 . . . . . аm1x1 + am2x2 + … amnxn ≤ bm. где bi-запас ресурса iго вида, x1≥0, x2≥0, ...xn≥0.
Математическая
модель задачи выглядит следующим
образом: найти производственную
программу (x1,
x2,
x3,
x4),
максимизирующую прибыль z
=
|
||||||||||||||||||||
|
15)Постановка общей задачи математического программирования. Задачу линейного программирования нередко формулируют как задачу минимизации или макси-мизации линейной формы L=c1x1+c2x2+...cnxn (1) при ограничениях x1≥0, x2≥0, ...xn≥0 и ∑ aijxj≤bi, i=1,2,...m1, ∑ aijxj=bi, i= m1+1, m1+2,...m2, ∑ aijxj≥bi, i= m2+1, m2+2,...m. Такую запись называют общей задачей линейного программирования. Обозначим через А матрицу системы линейных уравнений: а11x1 + a12x2 + … a1nxn = b1 а21x1 + a22x2 + … a2nxn = b2 (2) А = . . . . . аm1x1 + am2x2 + … amnxn = bm.
Через X и B – матрицы-столбцы (векторы) неизвестных и свободных членов:
а также введем в рассмотрение n-мерный вектор C = (с1 … сn), компонентами которого служат коэффициенты линейной формы (1), и n-мерный нуль-вектор 0(0, 0, …, 0). Тогда линейную форму можно рассматривать как скалярное произведение L=CX (3), систему линейных уравнений (2) заменить одним матричным уравнением AX=B (4), а условия x1≥0, x2≥0, ...xn≥0 записать в виде X≥0 (5). Поэтому часто основную задачу линейного программирования кратко записывают как задачу минимизации линейной формы (3) при линейных ограничениях (4) и (5). |
17)Многошаговые процессы решений в экономике. Динамическое программирование.Параметр состояния и функция состояния. Принцип оптимальности и рекуррентные соотношения. Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге. Принцип искать всегда оптимальное продолжение процесса относительно того состояния, которое достигнуто в данный момент, принято называть принципом оптимальности. Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления. |
19) Основные понятия в теории графов: дуги, вершины в ориентированном и неориентированном графе. Примеры применения теории графов на практике. Графом называется пара объектов, состоящая из множества точек и множества отрезков, соединяющих некоторые (может быть, все) из этих точек. Упомянутые точ-ки называются вершинами графа. Если отрезки, соединяющие вершины графа, имеют направления, то граф называ-ется ориентированным, а сами отрезки — дугами. Если же отрезки не имеют направ-ления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами. Смешанным называется граф, в котором содержатся как ориентированные, так и неориентированные отрезки. Ориентированный граф часто называют сетью. Обозначим
вершины графа
Две дуги графа (два ребра) называются смежными, если они различны и имеют общую вершину. Две вершины графа называются смежными, если существует дуга (ребро), соединяющая их. Говорят, что дуга исходит из вершины Xi, если Xi является ее началом. Дуга заходит в вершину Xj если Xj является ее концом. Говорят, что в графе данная дуга инцидентна данной вершине, если эта вершина является началом или концом данной дуги. Путь в ориентированном графе — это последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей. Путь, в котором ни одна вершина не встречается дважды, называется элементарным. Путь, в котором ни одна дуга не встречается дважды, называется простым, в противном случае — составным. Конечный путь, у которого конечная вершина совпадает с начальной, называется контуром. Контур, образованный одной дугой, называется петлей. Ориентированный граф называется симметрическим, если любые две смежные вершины его соединены двумя противоположно ориентированными дугами. Ориентированный граф называется антисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют. |
||||||||||||||||||||
|
20) Экономический смысл двойственной задачи к модели оптимального планирования производства. Математическая модель задачи определения расчетных оценок ресурсов. Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание. В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях. В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач. Если система ограничений исходной задачи состоит из неравенств и на все переменные хj наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач. Пусть исходная задача имеет вид: найти наибольшее значение функции
п Правило составления двойственных задач 1.
Каждому ограничению исходной задачи
ставится в соответствие двойственная
переменная yi,
где
2.
Составляется целевая функция
3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:
4. Переменные yi в двойственной задаче также неотрицательны, т.е.
Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным. В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.
|
16) Вектор-градиент, линия уровня, область допустимых решений в задаче ЛП. Геометрическая интерпретация задачи линейного программирования. Графическим методом решаются задачи ЛП с 2-мя переменными. Процесс решения происходит в 2 этапа. На первом этапе строится множество допустимых решений задачи. Допустимое решение – любой в-р, удовлетворяющий всем решениям задачи. Если первый этап закончился успешно, ищется оптимальное решение, которое представляет собой допустимое решение с наибольшим в задаче на максимум и с наименьшим в задаче на минимум значением целевой функции. Рассмотрим I-ый этап. Каждое ограничение типа рав-ва задает на плоскости прямую, а каждое линейное ограничение типа нерав-ва – полуплоскость. Для того, чтобы нарисовать полуплоскость сначала рисуют прямую, являющуюся ее границей. Для этого нерав-во превращают в рав-во и получают уравнение границы. Любая прямая однозначно задается любыми 2-мя точками, лежащими на ней. для того, чтобы найти такие точки одной из переменных придают произвольное значение, а значение другой переменной вычисляют из уравнения. Проще всего искать пересечение прямой с осями, при этом значение соответствующей переменной считается равной 0. После того, как граница полуплоскости построена надо выбрать одну полуплоскость из двух возможных. Для этого берется произвольная точка, не лежащая на границе полуплоскости. Лучше всего брать начало координат. Если координаты выбранной точки удовлетворяют нерав-ву, то выбирается полуплоскость, содержащая эту точку. Если же не удовлетворяют, то выбирается противоположная полуплоскость, не содержащая данной точки. Множество допустимых решений – это пересечение всех прямых, соответствующих линейным ограничениям типа рав-ва и всех полуплоскостей, соответствующих ограничениям типа нерав-ва. Если множ-во допустимых решений не пусто, то переходим ко II-му этапу. Выберем произвольное допустимое решение. Нарисуем из выбранного решения градиент целевой ф-ии. Для линейной функции градиент – это в-р, состоящий из коэффициентов этой ф-ии. Он показывает направление увеличения ф-ии. Через выбранное решение проводим линию уровня целевой ф-ии. Для линейной ф-ии линия уровня – это прямая, перпендикулярная градиенту. На линии уровня значение ф-ии постоянно. В задаче на max двигаем линию уровня параллельно самой себе в направлении градиента до последнего пересечения со множеством допустимых решений. В задаче на min линию уровня двигаем в направлении, противоположном направлению градиента. Возможны два случая: 1. последнее пересечение линии уровня со множ-вом доп. решений существует. Это пересечение и является множ-вом оптимальных решений. Для нахождения компонентов оптимальных решений составляем СЛАУ из уравнений границ, на пересечении которых лежит множ-во оптимальных решений, после чего решаем эту СЛАУ. 2. перемещать линию уровня во множ-ве доп. решений можно неограниченно. В этом случае оптимальных решений задача не имеет из-за неограниченности значений целевой ф-ии. С геометрической точки зрения вершина многоугольника – это точка пересечения двух смежных его сторон, а вершина многогранника – точка пересечения трех смежных его граней. Сторонами (гранями) служили границы ограничений задачи. Задача ЛП состоит в отыскании таких точек многоугольника решений, координаты которого обеспечивали бы линейной ф-ии минимальное или максимальное значение. С геометрической точки зрения вершина многоугольника – это точка пересечения двух смежных его сторон, а вершина многогранника – точка пересечения трех смежных его граней |
В экономике и управлении часто встречаются ситуации, в которых сталкиваются две или более стороны, преследующие различные цели, причем результат, полученный каждой из сторон при реализации определенной стратегии зависит от действий других сторон. Такие ситуации называются конфликтными. Например: аукцион, спортивные состязания, парламентские выборы (при наличии нескольких кандидатов), карточная игра. Рассмотрим конфликт двух участников с противоположными интересами. Математической моделью такого конфликта является игра с нулевой суммой. Участники игры называются игроками. Стратегией игрока называется осознанный выбор одного из множества возможных вариантов его действий. Рассмотрим конечные игры, в которых множества стратегий игроков конечны; стратегии первого игрока пронумеруем от 1 до m, а стратегии второго игрока — от 1 до n. Если первый игрок выбрал свою i-ю стратегию, а второй игрок — свою j-ю стратегию, то результатом такого совместного выбора будет платеж второго игрока первому. Таким образом, игра с нулевой суммой однозначно определяется матрицей, которая называется платежной. Строки этой матрицы соответствуют стратегиям первого игрока, а столбцы — стратегиям второго игрока. Игра происходит партиями. Партия игры состоит в том, что игроки одновременно называют свой выбор: первый игрок называет некторый номер строки матрицы, а второй — некоторый номер столбца этой матрицы. После этого происходит «расплата». Пусть, например, первый игрок назвал номер i, а второй — j. Тогда второй игрок платит первому сумму. На этом партия игры заканчивается. Если aij>0, то это означает, что при выборе первым игроком i-й стратегии, а вторым — j-й стратегии выигрывает первый игрок. Цель каждого игрока — выиграть как можно большую сумму в результате большого числа партий. Стратегия называется чистой, если выбор игрока неизменен от партии к партии.
При
любой стратегии первого игрока, второй
игрок будет выбирать стратегию
обеспечивающий ему наибольший выигрыш,
поэтому с точки зрения первого игрока
надо выбирать такую стратегию, при
которой второй игрок, действуя разумно
заплатит наибольшую сумму. Такая
стратегия первого игрока называется
максиминной,
а величина
Аналогично
(с точки зрения второго игрока)
определяется верхняя
цена игры
В общем случае имеет место неравенство α≤β, если же α=β, то говорят, что игра имеет седловую точку, общее значение и β называется при этом ценой игры. При этом стратегии игроков, соответствующие седловой точке, называются оптимальными чистыми стратегиями, так как эти стратегии являются наиболее выгодными сразу для обоих игроков.
Смешанной
стратегией первого
игрока называется вектор
Пусть
игроки – Первый и Второй, играют в
матричную игру с матрицей
Если игроки применяют свои смешанные стратегии P (p1, p2,…pm )и Q (q1, q2,…qn) соответственно, Выигрыш первого: выигрыш aij Вероятность pi qj.
То
есть первый игрок с вероятностью pi
gj.
выигрывает
aij..
Математическое
ожидание выигрыша первого игрока
равно М(P,Q)=
И это равно математическому ожиданию проигрыша второго игрока.
Пусть
Предположим
сначала, что игроки озабочены только
максимизацией среднего дохода за
партию игры – обычная цель в таких
играх. Тогда игроки будут играть со
своими оптимальными
стратегиями:
Пара
(P*,Q*)
– решение игры. Математическое
ожидание с. в.
|
||||||||||||||||||||
|
22)Сформулировать и доказать критерий оптимальности решения задачи линейного программирования при отыскании минимума линейной функции симплексным методом. В частном случае общей задачи ЛП система уравнений имеет предпочитаемый вид, при этом правые части всех уравнений неотрицательны. Допустим необходимо минимизировать целевую функцию L=c1x1+c2x2+...cnxn (1), при условиях:
x2 + g2,m+1 xm+1 + ... + g2nxn = h2, (2) ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm и xj≥0, j = 1,2,...n (3). Для решения такой задачи применяется симплексный метод линейного программирования. Одним из допустимых решений задачи ЛП будет базисное неотрицательное решение системы (2): x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (4), ему соответствует значение целевой ф-ии равное:
L0=c1h1+c2h2+...cmhm+cm+1*0+...+cn*0
=
Надо исследовать, является ли базисное неотрицательное решение (4) оптимальным,т.е. является ли значение (5) наименьшим из всех возможных значений целевой ф-ии (1), отвечающих различным неотрицательным решениям системы (2). Учитывая, что система уравнений (2) имеет предпочитаемый вид, находим для нее общее решение: xi=hi-gi,m+1xm+1-...-ginxn, i=1,2,...,m (6). Если свободным неизвестным придавать какие-нибудь неотрицательные значения, то будем получать различные решения системы (2), среди которых нас интересуют только неотрицательные. Подставляя их компоненты в линейную форму (1), можно подсчитать соответствующие значения целевой функции. Очевидно, чтобы легче было следить за поведением целевой функции, целесообразно выразить ее только через свободные неизвестные. Если переписать выражение (1) в виде:
-
L+c1x1+c2x2+...cmxm+
cm+1xm+1+...+cnxn=0
(7). Для того чтобы исключить базисные
неизвестные из этого уравнения,
достаточно умножить первое уравнение
системы (2) на c1,
второе на c2
и т.д., сложить полученные произведения
и из результата вычесть уравнение
(7). Получим L+∆m+1xm+1+...+∆nxn=L0
(8), где ∆j
= c1g1j
+ c2g2j
+ ... + cmgmj
- cj
, j=1,2,...n
(9) или ∆j
= zj
- cj,
zj= Из выражения следует, что базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (2) является оптимальным решением задачи ЛП Базисное решение является оптимальным решением задачи ЛП тогда и только тогда, когда в уравнении среди коэффициентов при неизвестных нет ни одного положительного, т. е. условие оптимальности имеет вид ∆j≤0 , j=1,2,…,n. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения. Очевидно, оптимальных решений будет еще больше, если среди коэффициентов при свободных неизвестных в уравнении (8) окажется несколько нулевых. |
21) Сформулировать и доказать критерий оптимальности решения задачи линейного программирования при отыскании максимума линейной функции симплексным методом. Все дв. оценки ≥ 0. Но дв. оценки – это взятые с противоположным знаком коэффициенты выражения ц.ф. через свободные неизвестные. Значит, сами эти коэффициенты ≤ 0. Поэтому, как только любая из свободных неизвестных примет положительное значение – целевая функция уменьшается. А это и означает, что она максимальна при нулевых значениях св.неизвестных, т.е. для данного базисного решения. + 22 вопрос, тока min меняем на max
34.В каком случае процесс решения задачи ЛП симплекс-методом является конечным. Один шаг симплекс-метода состоит в работе с конкретным базисным решением и заключается в следующем: 1)вычисляется симплекс-разности для всех свободных переменных: cj-cBqj , j=m+1, m+n; 2)определяется максимальная симплекс-разность cs –cBqs =max (cj- cBqj ) m+1≤j≤m+n (если разность положительна,переходим к след пункту,если нет то алгоритм закончен) 3)в базис вводится переменная Хs, а выводится переменная Xr, для которой
Эти шаги повторяются до тех пор,пока на некотором шаге все симплекс-разности станут неположительными.Тогда оптимальное решение получено. |
23)В каком случае базисное оптимальное решение задачи линейного программирования будет ее единственным оптимальным решением? Ответ обосновать В частном случае общей задачи ЛП система уравнений имеет предпочитаемый вид, при этом правые части всех уравнений неотрицательны. Допустим необходимо минимизировать целевую функцию L=c1x1+c2x2+...cnxn (1), при условиях:
x2 + g2,m+1 xm+1 + ... + g2nxn = h2, (2) ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm и xj≥0, j = 1,2,...n (3). Для решения такой задачи применяется симплексный метод линейного программирования. Из выражения L=L0-∆m+1xm+1-...-∆nxn (1) следует, что базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (2) является оптимальным решением задачи ЛП Базисное решение является единственным оптимальным решением задачи ЛП тогда и только тогда, когда в уравнении среди коэффициентов при неизвестных нет ни одного положительного, т. е. условие оптимальности имеет вид ∆j≤0 , j=1,2,…,n. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения. Очевидно, оптимальных решений будет еще больше, если среди коэффициентов при свободных неизвестных в уравнении (1) окажется несколько нулевых. Если есть хотя бы одна свободная неизвестная, такая что коэффициент ∆j при ней в последнем уравнении системы
положителен, а в первых m уравнениях той же системы среди коэффициентов g1j, g2j, …gmj при ней нет ни одного положительного, то задача линейного программирования неразрешима в силу неограниченности линейной формы L=c1x1+c2x2+...cnxn на множестве неотрицательных решений системы ограничений
|
||||||||||||||||||||
|
26) В каком случае при решении задачи линейного программирования симплекс-методом значения линейной функции двух последовательных планов могут совпасть? П0 Х0 Х3 Х5 Х7 β Х1 1 -1 0 0 Х5 * 0 -3 1 0 Х7 0 -4 0 1 1240 -10 -10/3
1240 – β • * ≠ 0 Значения линейной функции двух последовательных планов могут совпадать, если среди базисного плана есть 0 – вырожденный план
|
25) В каком случае задача оптимального производственного планирования не имеет оптимального плана? «задача оптимального производственного планирования» - «линейного производства» («≤», max).
О Х1 300 1 -1 0 0
Х5 250 0 -3 1 0 0 Х7 0 -4 0 1 -4 1 -10
250 = - 3Х3+Х5 Х5=250 + 3Х3 |
31.Правила выбора ключевого столбца и строки при решении задачи ЛП симплексным методом, последствия неправильного выбора. 1)Ключевой столбец выбираем по минимальной двойственной оценке 2)Потом считается столбец альфа3)По минимальной альфа выбираем ключевую строку
32.Введение балансовых переменных в систему ограничений задачи ЛП: цель и правило введения. “балансовые”=”дополнительные”-чтобы приравнять неравенство в равенство. Правило: ≤ +Х7 ≥ -Х7
|
||||||||||||||||||||
|
24)Доказать, что в случае отсутствия вырождения в задаче линейного программирования на нахождение минимума линейной функции преобразования по симплекс-методу приводят к конечной последовательности монотонно убывающих значений линейной функции.
В
частном случае общей задачи ЛП система
уравнений имеет предпочитаемый вид,
при этом правые части всех уравнений
неотрицательны.Для того чтобы при
последовательном исключении неизвестных
для приведения СЛАУ к предпочитаемому
виду или перехода от одного предпочитаемого
вида к другому свободные члены всех
уравнений системы оставались
неотрицательными, необходимо
руководствоваться следующими правилами
выбора разрешающей неизвестной и
разрешающего уравнения. В качестве
разрешающей неизвестной можно принять
любую неизвестную, при которой есть
хоть один положительный коэффициент,
а затем в качества разрешающего
уравнения следует взять то уравнение,
которое соответствует наименьшему
среди отношений свободных членов
уравнений к соответствующим положительным
коэффициентам при выбранной неизвестной
в этих уравнениях. СЛАУ подвергается
симплексным преобразованиям, если
процесс исключения неизвестных
осуществляется в соответствии с
указанными правилами выбора разрешающей
неизвестной и разрешающего уравнения.Может
случиться, что указанное минимальное
отношение достигается при нескольких
значениях индекса i.
Тогда любое из соответствующих им
уравнений можно принять за разрешающее.
Принято говорить в этом случае, что
рассматриваемая СЛАУ является
вырожденной. Вырожденной
СЛАУ называют
такую систему, у которой в какой-либо
предпочитаемой форме хотя бы один
свободный член ранен нулю.Остается
заметить, что СЛАУ не будет иметь ни
одного неотрицательного решения, если
в процессе симплексных преобразований
в ней появится уравнение, в котором
свободный член строго положителен, а
среди коэффициентов при неизвестных
нет ни одного положительного.Если
в процессе решения задачи ЛП
симплекс-методом найдется хотя бы
одна свободная неизвестная xj
такая, что ∆j>0,
а коэффициенты
30)Для задачи линейного программирования … получить выражение целевой функции z через свободные переменные общего решения системы ограничений.
C3 П3 Н0 Х1 Х2 Х3 Х4 Х5 Х6 Х7 3 Х2 1
0 Х6 1
5 Х3 1 -z+1400 Двойственные оценки Коэффициент выражения ц.ф-и через свободные переменные – это двойственные оценки (с точностью до знака) Правило: столбец С3 * столбец матрицы, а затем вычетается верхнее значение наверху. Док-во: правила вычисления двойственных оценок. Без ограничений общности, базисными стали Х1, Х2, Х3.
C3П3 Н0 Х1 Х2 Х3 Х4 Х5 Х6 Х7
Х1 1 S
Х2 1
Х3 1 Двойственные оценки
F = CX= C1X1+ C2X2= C1*X1 + C2*X2= C1(H-SX2) + C2( H2) = C1H + (-C1S + C2)X2= Z0+(-C1S + C2)X2=Z0-(C1S- C2)X2=Z Z= Z0-(C1S- C2)X2 40=X1+ 7X4+2X1 H=X1+SX2→X1=H-SX2 |
27) Сформулировать и доказать условие неограниченности целевой функции на множестве допустимых решений при решении задачи линейного программирования симплекс-методом. В частном случае общей задачи ЛП система уравнений имеет предпочитаемый вид, при этом правые части всех уравнений неотрицательны. Д x1 + g1,m+1xm+1 + ... + g1nxn = h1, x2 + g2,m+1 xm+1 + ... + g2nxn = h2, (2) ... ... ... ... xm + gm,m+1 xm+1 + ... + gmnxn = hm и xj≥0, j = 1,2,...n (3). Для решения такой задачи применяется симплексный метод линейного программирования. Из выражения L=L0-∆m+1xm+1-...-∆nxn (1) следует, что базисное решение x1=h1, x2=h2,...xm=hm, xm+1=0,...xn=0 (2) является оптимальным решением задачи ЛП Базисное решение является единственным оптимальным решением задачи ЛП тогда и только тогда, когда в уравнении среди коэффициентов при неизвестных нет ни одного положительного, т. е. условие оптимальности имеет вид ∆j≤0 , j=1,2,…,n. Если же хотя бы один из коэффициентов при свободных неизвестных равен нулю, то будут и небазисные оптимальные решения. Очевидно, оптимальных решений будет еще больше, если среди коэффициентов при свободных неизвестных в уравнении (1) окажется несколько нулевых. Если есть хотя бы одна свободная неизвестная, такая что коэффициент ∆j при ней в последнем уравнении системы
положителен, а в первых m уравнениях той же системы среди коэффициентов g1j, g2j, …gmj при ней нет ни одного положительного, то задача линейного программирования неразрешима в силу неограниченности линейной формы L=c1x1+c2x2+...cnxn на множестве неотрицательных решений системы ограничений |
28)сформулировать теорему связи решений исходной и вспомогательной задач при решении задачи линейного программирования методом искусственного базиса: Метод искусственного базиса применяется к решению задач линейного программирования в общем случае, когда система ограничений не имеет предпочитаемого вида. Пусть
требуется минимизировать
К данной задаче ЛП непосредственно нельзя применить симплексный метод, т.к. система (2) не имеет предпочитаемого вида, хотя правые части всех ее уравнений можно считать неотрицательными. Поэтому к левой части каждого уравнения системы (2) добавим по одной искусственной неотрицательной неизвестной и образуем следующую систему m линейных уравнений с n+m неизвестными:
где
Очевидно,
в системе (4) неизвестные
Для
решения вспомогательной задачи можно
применить симплексный метод, так как
система (4) имеет предпочитаемый вид,
искусственные неизвестные Если Smin<0, то исходная задача не имеет решения ввиду противоречивости условий (2) и (3). Действительно, если допустить, что система уравнений (2) имеет неотрицательное решение (α1,α2,...,αn), то вспомогательная задача будет иметь решение (α1,α2,...,αn,0,0,…,0) для которого S=0, что противоречит предположению. Если же S=0, то возможна дальнейшая минимизация. |
||||||||||||||||||||
|
33.Применение искусственных базисных неизвестных к решению основной задачи ЛП. Условие противоречивости системы условий исходной задачи. Метод искусственного базиса применяется к решению задач линейного программирования в общем случае, когда система ограничений не имеет предпочитаемого вида.
Пусть
требуется минимизировать
К данной задаче ЛП непосредственно нельзя применить симплексный метод, т.к. система (2) не имеет предпочитаемого вида, хотя правые части всех ее уравнений можно считать неотрицательными. Поэтому к левой части каждого уравнения системы (2) добавим по одной искусственной неотрицательной неизвестной и образуем следующую систему m линейных уравнений с n+m неизвестными:
где
Очевидно,
в системе (4) неизвестные
Для
решения вспомогательной задачи можно
применить симплексный метод, так как
система (4) имеет предпочитаемый вид,
искусственные неизвестные Если Smin<0, то исходная задача не имеет решения ввиду противоречивости условий (2) и (3). Действительно, если допустить, что система уравнений (2) имеет неотрицательное решение (α1,α2,...,αn), то вспомогательная задача будет иметь решение (α1,α2,...,αn,0,0,…,0) для которого S=0, что противоречит предположению. Если же S=0, то возможна дальнейшая минимизация |
56)Записать алгоритм решения транспортной задачи (перечислить по порядку этапы решения). Обосновать конечность метода потенциалов решения транспортной задачи.
Конечность метода потенциалов – метод потенциалов всегда приводит к оптимальному плану |
35.В каких задачах находится симплекс-метод? В задачах линейного программирования.Для задач,связанных с принятием решений в экономике,характерна ситуация,когда требуется достичь некоторой цели при ограниченных ресурсах.Если функция цели линейно зависит от переменных (размеров видов деятельности или производственных процессов) и расходы ресурсов также линейно зависят от переменных,то такая задача принятия решений сводится к задаче линейного программирования(ЛП).
36.Что представляет собой симплексная таблица Симплекс-таблица составляется из коэффициентов при x1, x2, x3, x4 и чисел, стоящих в правых частях уравнений-ограничений задачи: в первой строке записываются элементы уравнения (А), во второй - (В). В последней строке симплекс-таблицы записываются коэффициенты и правая часть целевой функции (С). Таким образом, симплекс-таблица содержит две строки коэффициентов (по числу ограничений задачи) и строку коэффициентов целевой функции. Число столбцов в симплекс-таблице равно числу переменных задачи плюс один столбец правых частей (b):
37.Запишите симметричную пару двойственных задач линейного программирования. Прямая задача имеет ограничение ≤, целевая функция максимальна Двойственная ≥,цифровая функция минимальна 2х1+3х2+8х3≥50 y1 4х1-7х2+9х3≤ у2 F=100х1+200х2+300х3=>max Х1,2,3≥0
2у1+4у2≥100 3у1-7у2≥200 8у1+9у2≥300 G=50у1+60у2=>min
|
||||||||||||||||||||
|
38.Двойственные (расчетные) оценки ресурсов. Симметричная пара двойственных задач ЛП. Несимметричная пара двойственных задач ЛП, правила составления двойственной задачи для данной задачи ЛП со смешанными ограничениями. Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание. В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях. В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач. Если система ограничений исходной задачи состоит из неравенств и на все переменные хj наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач. Пусть исходная задача имеет вид: найти наибольшее значение функции
при ограничениях:
Правило составления двойственных задач 1.
Каждому ограничению исходной задачи
ставится в соответствие двойственная
переменная yi,
где
2.
Составляется целевая функция
4. Переменные yi в двойственной задаче также неотрицательны, т.е.
Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку. |
39.Матричная запись пары двойственных задач ЛП (симметричная пара задач с ограничениями-неравенствами и нессиметричная пара,где в одной из задач ограничения имеют вид равенств) Прямая Двойствен AX≤И A*Y≥C х≥0 Y≥0 F=CX=>max G=B*Y=>min
Если среди неравенств есть 1 равенство,то нессиметричная пара. 2х1+3х2+8х3≤50 у1 4х1-7х2+9х3=60 у2
44.Вторая основная теорема двойственности (о дополняющей нежесткости) и ее экономическое истолкование.
Для
того чтобы допустимые решения исходной
Т.е. если какое-либо нер-во системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна быть равна 0. Если же какая-либо компонента оптимального решения положительна, то соотв-ее ей ограничение в двойственной задаче должно быть обращено в точное равенство.
Другими
словами: 1)если хj0>0,то
Если по оптимальному плану расход i-того ресурса < его запасов, то оценка этого ресурса=0. Если же оценка>0, то расход этого ресурса равен его запасу. Таким образом, дефицитный (полностью используемый по оптимальному плану) ресурс имеет положительную оценку в двойственной задаче, а недефицитный – нулевую оценку. С точки зрения пр-ва: если оценка ресурсов, расходуемых по j-ой технологии больше цены продукта, то j-ая технология не применяется (xj=0). Если же по некот. плану j-ая технология применяется (xj>0), то оценка ресурсов, расходуемых по данной технологии, равна цене продукта. Эта т-ма вместе с еще 2-мя теоремами и образует так называемую т-ию двойственности ЛП |
40,41,42.Основное неравенство теории двойственности ЛП. Малая теорема двойственности и ее экономическое содержание. Теорема о достаточном условии оптимальности решений пары двойственных задач ЛП.
Для
любых допустимых решений
Малая теорема двойственности: Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них.
Теорема
о достаточном условии оптимальности
решений пары двойственных задач: Если
Согласно этой теореме, план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.
43.Первая основная теорема двойственности и ее экономическое истолкование. Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание. Если
одна из двойственных задач имеет
оптимальное решение, то двойственная
ей задача также имеет оптимальное
решение, причем экстремумы целевых
функций равны, т.е.
Если одна из двойственных задач не имеет оптимального решения, то другая задача также не имеет оптимального решения, причем если одна из задач не имеет оптимального решения из-за неограниченности целевой функции, то другая из-за несовместности системы ограничений. Связь между задачами двойственной пары глубже, чем указано в формулировке теоремы. Оказывается, что симплексный метод, примененный к одной из задач, автоматически приводит к решению другой задачи. Экон.смысл: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения минимальных оценок ресурсов, причем цена продукта, полученного при реализации оптимального плана, совпадает с суммарной оценкой имеющихся ресурсов. Совпадение значений целевых функций для соответствующих решений пары двойственных задач является достаточным условием оптимальности этих решений. Эта т-ма вместе с еще 2-мя теоремами и образует так называемую т-ию двойственности ЛП.
46.В чем состоит условие устойчивости двойственных оценок? Область устойчивости двойственных оценок B=>B+T, область устойчивости-множество значений (t1,t2) на двумерной плоскости. -A2T≤Hопт T =t1 t2 Hопт=A2B Hопт=A2(B+T)=0 A2B+A2T≥0 -A2T≤ Hопт |
||||||||||||||||||||
|
45.Третья основная теорема двойственности (об оценках влияния ресурсов на выпуск продукции) и ее экономическое содержание (без доказательства). Перераспределение ресурсов между предприятиями фирмы с помощью двойственных оценок ресурсов.
Значения
переменных yi0
в оптимальном решении двойственной
задачи представляют собой оценки
влияния свободных членов (правых
частей bi)
системы
ограничений исходной задачи на величину
максимума целевой функции:
Экон.смысл:
двойственная оценка ресурса – это
приращение прибыли, приходящейся на
единицу приращения этого ресурса.
Здесь речь
идет лишь о достаточно малых приращениях
ресурсов, так как изменение величины
Эта т-ма вместе с еще 2-мя теоремами и образует так называемую т-ию двойственности ЛП. Из 2-ой и 3-ей теорем следует, что часть ресурсов, у которых двойственные оценки будут отличны от 0, необходимо будет пополнять для продолжения выпуска продукции. Недостающие ресурсы должны быть пополнены, причем в оптимальном количестве. |
48) Постановка и математическая модель транспортной задачи, число базисных неизвестных. Записать основные свойства этой модели. Сначала рассмотрим случай,когда суммарные запасы продукции поставщиков = суммарным запросам потребителей: ∑ai=∑bj Транспортная задача,в которой выполняется это условие,называется сбалансированной,закрытой или замкнутой.В этом случае удовлетворение запросов всех потребителей возможно,если от каждого поставщика вывозится вся продукция , а каждому потребителю продукция доставляется в количестве, соответствующем его запросам.Очевидно,что математической моделью закрытой транспортной задачи будет следующая задача ЛП: m n L=∑ ∑ cijxij->min i=1 j=1 ∑xij=ai, i=1,…1m, j=1 ∑xij=bj, j=1,…,n, i=1 xij≥0, i=1,…,m; j=1,…,n. Отметим 2 важных свойства задачи (1.2)-(1.5): 1)задача всегда имеет решение 2)ранг матрицы коэффициентов системы уравнений (1.6),(1.4) равен m+n-1. |
47.Условие сохранения структуры производственной программы и двойственных оценок ресурсов при изменении объемов ресурсов. Задача о «расшивке узких мест производства», ее математическая модель и решение. Двойственная оценка ресурса — это приращение прибыли, приходящееся на единицу приращения этого ресурса. Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта. В задаче планирования производства находится оптимальный план пр-ва и узкие места пр-ва, т.е. те ресурсы кот. используются полностью, а потому называются дефицитными. Расшивка «узких мест» пр-ва подразумевает заказ дополнительно дефицитных ресурсов. Пусть T(t1,t2,…,tm) - вектор дополнительных объемов ресурсов, (В+Т) – вектор новых объемов ресурсов. Прирост прибыли, приходящийся на ti единиц i-го ресурса, будет равен уiti, где уi- двойственная оценка этого ресурса. Cледует иметь ввиду, что найденными двойственными оценками ресурсов мы можем пользоваться только при таких изменениях объемов ресурсов и, соответственно, компонент оптимального плана, когда сохраняется структура плана производства и остаются постоянными двойственные оценки ресурсов. Условие устойчивости двойственных оценок, как видно из соотношения Q-1B=H, характеризуется неравенством: H+Q-1T≥0 Составить план расшивки узких мест пр-ва означает указать сколько единиц каждого из дефицитных ресурсов нужно дополнительно заказать, чтобы суммарный прирост прибыли был максимальным. Т.о. проблема расшивки «узких мест» представляет собой задачу линейного программирования: найти план расшивки T(t1, t2,…, tm), максимизирующий суммарный прирост прибыли: w = y* T, при условиях H+Q-1T>=0 и T>=0. |
||||||||||||||||||||
|
51.Методы построения первого базисного решения транспортной задачи. Транспортная задача формулируется следующим образом. Продукт, сосредоточенный в m пунктах производства в кол-ве a1, a2,...,am единиц, необходимо распределить между n пунктами потребления, которым необходимо b1,b2,..,bn единиц. Стоимость перевозки единицы продукта из i-го пункта пр-ва в j-ый пункт потр-ия равна cij. Необходимо составить план перевозок, при кот. запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах пр-ва и общие транспортные расходы по доставке были бы минимальны. Первое базисное допустимое решение легко построить по правилу северо-западного угла. В соответствии с этим правилом, заполнение транспортной таблицы начинается с левой верхней клетки и состоит из однотипных шагов, на каждом из которых из рассмотрения исключается один поставщик или один потребитель:
После этого рассматривается левая верхняя клетка среди тех, которые остаются после вычеркивания строк, соответствующих поставщикам, весь запас продукта у которых уже распределен по потребителям, и столбцов, соответствующих потребителям, запросы которых уже удовлетворены.
Каждому
поставщику ставится в соответствие
потенциал
pi,
а каждому потребителю — потенциал
qi.
При этом каждой клетке соответствует
некоторая оценка:
Один из потенциалов можно выбрать произвольно, так как в системе одно уравнение линейно зависит от остальных. Обычно полагают p1=0. Остальные потенциалы вычисляются из условия, что для базисных клеток ∆ij=0.
Затем
вычисляются оценки всех свободных
клеток. Если хотя бы одна из оценок
строго положительна, то базисное
допустимое решение, содержащееся в
данной транспортной таблице, не
является оптимальным. Выбирается
свободная клетка (r,
s),
соответствующая наибольшей положительной
оценке
Для выбранной свободной клетки строится цикл пересчета — замкнутая ломаная, одна из вершин которой находится в данной свободной клетке, а все остальные — в занятых клетках, соседние звенья взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы. Так производится перераспределение поставок вдоль цикла пересчета, при котором происходит такой переход к новому базисному допустимому решению. |
49.Постановка и математическая модель транспортной задачи,в которой суммарные запасы продукции меньше суммарныхъ запросов на нее.Записать правила сведения такой модели к замкнутой задаче и записать полученную замкнутую модель транспортной задачи. Правило:Если суммарная мощность меньше суммарного спроса,то вводится фиктивный поставщик,его мощность=тому чего не хватает.В таблице вводится доп. строка,затраты считаются 0. 50. Постановка и математическая модель транспортной задачи,в которой суммарные запасы продукции больше суммарныхъ запросов на нее.Записать правила сведения такой модели к замкнутой задаче и записать полученную замкнутую модель транспортной задачи. Правило:Если суммарная мощность меньше суммарного спроса,то вводится фиктивный потребитель,его мощность=тому чего не хватает.В таблице вводится доп. строка,затраты считаются 0
54.правило расчета потенциалов поставщиков и потребителей в транспортной задаче.Расчет оценочных коэффициентов для свободных клеток транспортной задачи.Условие оптимальности базисного решения. Ui+Vj=Cij Задается начальный потенциал,потом по кружкам вычисляют. Условие: Базисное решение в транспортной задаче- определ вариант распределенных базисных поставок,число кружков=m+n-1.Кружки должны образовывать вычеркиваемую комбинацию. Условие-хар-ки свободных клеток должны быть положительными.
|
52.Записать правила построения первого базисного решения замкнутой транспортной задачи по методу минимального элемента в матрице тарифов(издержек). При построении первого базисного решения по этому методу первой заполняется клетка с минимальным значением Сij и в нее заносится максимально возможное значение Хij. Далее по тем же правилам, что и в методе “северо-западного угла”, исключается один из участников (всегда только 1), находится минимальный из оставшихся элементов Сij и в соответствующую клетку записывается максимально возможное для этой клетки значение Хij. Процесс продолжается до получения базисного решения. При этом заполненными окажутся (m+n-1) клеток. Замечание.Базисность допустимых решений, получаемых с помощью указанных выше методов,обеспечивается автоматически в случае выполнения следующих рекомендаций: 1)при заполнении очередной клетки необходимо присваивать соответствующей переменной максимально возможное значение 2)после заполнения очередной клетки исключается из дальнейшего рассмотрения один и только один участник
|
||||||||||||||||||||
|
53.Записать математическую модель замкнутой транспортной задачи, составить двойственную к ней задачу и записать условия второй основной теоремы двойственности для получения пары взаимодвойственных задач ЛП. Сначала рассмотрим случай,когда суммарные запасы продукции поставщиков = суммарным запросам потребителей:
∑ai=∑bj Транспортная задача,в которой выполняется это условие,называется сбалансированной,закрытой или замкнутой.В этом случае удовлетворение запросов всех потребителей возможно,если от каждого поставщика вывозится вся продукция , а каждому потребителю продукция доставляется в количестве, соответствующем его запросам.Очевидно,что математической моделью закрытой транспортной задачи будет следующая задача ЛП: m n L=∑ ∑ cijxij->min i=1 j=1 ∑xij=ai, i=1,…1m, j=1 ∑xij=bj, j=1,…,n, i=1
xij≥0, i=1,…,m; j=1,…,n.
Отметим 2 важных свойства задачи (1.2)-(1.5): 1)задача всегда имеет решение 2)ранг матрицы коэффициентов системы уравнений (1.6),(1.4) равен m+n-1. Задача,двойственная к транспортной задаче. Пусть дана закрытая транспортная задача,математическая модель которой имеет вид (1.2)-(1.5).Составим двойственную задачу.Обозначим переменные двойственной задачи,соответствующие уравнениям (1.3) через Pi (i=1,...,m),а переменные, соответствующие уравнениям (1.4)-через Qj(j+1,…,n). Тогда задача,двойственная к задаче (1.2)-(1.5), примет вид m m ∑aipi+∑bjqi->max i=1 j=1 pi+qj≤cij, i=1,…,m; j=1,..,n.
Задача (1.6),(1.7)содержит(mn) неравенств (1.7) относительно (m+n) неизвестных Pi и Qj ,которые могут принимать значения любого знака. Из второй основной теоремы двойственности получаем,что допустимое решение Хij (i=1,…,m; j=1,…,n) задачи (1.2)-(1.5) и допустим решение Pi(i=1,…,m) и Qj (j=1,…,n) задачи (1.6)-(1.7) будут оптимальными решениями соответствующих задач тогда и только тогда,когда они будут удовлетворять следующим условиям: n pi(∑xij-ai)=0,i=1,…,m j=1 m qj(∑xij-bj)=0,j=1,…,n i=1 xij(pi+qj-cij)=0, i=1,..,m; j=1,..,n
Отметим что для нашей нессиметричной пары взаимодвойственных задач условия (1.8) и (1.9) выполняются для любых допустимых решений задачи (1.2-1.5),поэтому условия (1.8-1.9) не накладывают никаких ограничений на Pi и Qj.Также на консультации разбирали(смотрите тетрадь) |
57.Объяснить смысл перевозок от фиктивного поставщика или к фиктивному потребителю в оптимальном решении транспортной задачи. Для сведения открытой задачи к закрытой вводятся фиктивные пункты производства или потребления. Если суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, вводится фиктивный потребитель, у которого объем потребления равен разнице между объемом производства и объемом потребления; если же суммарные запасы продукта у поставщиков строго больше, чем суммарные запросы потребителей, то вводится фиктивный поставщик.
Обозначим
через хij
количество груза, планируемого к
перевозке от i-го
поставщика j-му
потребителю. При наличии баланса
производства и потребления
Х
= (хij),
минимизирующий
общую стоимость всех перевозок
пункта
производства вывозится весь продукт:
|
55.Записать определение цикла пересчета в транспортной таблице. Использование цикла пересчета для получения нового(улучшенного) базисного решения. Циклом пересчета,соответствующим данной свободной клетке транспортной задачи,называется замкнутая ломаная линия,одна вершина которой лежит в этой свободной клетке, а остальные вершины- в занятых базисных клетках транспортной таблицы. Полученная ломаная должна удовлетворять следующим условиям: а)ее звенья параллельны строкам или столбцам таблицы; б)в каждой вершине ломаной под прямым углом сходятся два ее звена. Доказано,что для любой свободной клетки транспортной таблицы существует единственный цикл пересчета, который может быть представлен и самопересекающейся ломаной,но точки ее самопересечения по определению цикла пересчета не являются его вершинами. Построим цикл пересчета для выделенной нами клетки (i0,j0). Запишем в клетку с номером (i0,j0) знак “+”,в соседнюю клетку с номером (i0,j1)-знак “-“.Так, двигаясь вдоль цикла пересчета, будем в вершинах цикла поочередно ставить знаки “+” или знаки “-”.Очевидно, что число вершин цикла пересчета всегда четно. Поэтому не имеет значения, в какую из двух соседних клеток был осуществлен переход из клетки с номером(i0,j0).Изменим теперь поставки в вершинах цикла пересчета в соответствии со знаками , находящимися в этих вершинах, на величину w.Тогда поставки примут значение xi0+w, xi0j1-w, xi1j1-w,…,xikjk-w, xikj0-w. Присвоим величине w значение, равное Хisjs-w окажется равной 0. Соответствующую неизвестную Хisjs переводим в разряд свободных, а клетка с номером (is,js) остается пустой.В итоге будет получено новое базисное решение,которое исследуется на оптимальность тем же методом. Покажем,что в новом базисном решении значение целевой функции-суммарные транспортные расходы-не возрастает по сравнению с ее значением для старого базисного решения.Найдем приращение DL целевой функции.Так как изменение поставок на величину w происходит только в вершинах цикла пересчета,то, представим величину DL в виде |
||||||||||||||||||||
|
58.Что такое целочисленное линейное программирование? Допустимое множество задачи ЦЛП. К задачам ЦЛП относят задачи с линейной целевой функцией и линейными ограничениями, в которых на все переменные наложены условия целочисленности. 59.Что такое параметрическое линейное программирование?Где может находиться параметр? Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров. Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, что-бы в результате решения иметь наилучшие планы для любого варианта исходных данных. С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения. Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ. Коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.). |
|
60. Что такое многокритериальная задача. Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (стоимость, надежность и т.п.) Математически такая задача содержит область допустимых решений, которая может иметь любую природу, и несколько целевых функций, значение которых должно максимизироваться или минимизироваться в данной области. Максимизация и минимизация целевых функций легко сводятся друг к другу умножением на -1, поэтому, не нарушая общности, можно считать, что данная задача имеет вид:
F x € D x - ? , где D- область допустимых значений
|
||||||||||||||||||||
|
61. Что такое рекорд в методе ветвей и границ. Рекорд- это такое оптимальное значение целевой функции на частичной задачи, которое позволяет оставшиеся части более не рассматривать. 62. Приведите пример задачи целочисленного линейного программирования Решить задачу ЦЛП: f(x1,x2)= 2x1+3x2 → max, 5x1+7x2 ≤ 35, 4x1+9x2 ≤ 36, x1, x2 ≥ 0, x1,x2 - целые Задачу решить можно методом прямого перебора. Организуем 2 цикла: 1-й по x1 от 0 до 9, 2-й, встроенный в первый, - по x2 от 0 до 5. Оператор тела цикла проверяет, удовлетворяет ли точка (x1, x2) обоим неравенствам, вычисляется значении функции f(x1, x2) и сравнивается с запомненным наилучшим решением. 63. Приведите пример задачи параметрического линейного программирования Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров. Рассмотрим задачу минимизации L(X, λ) = λX1 - λX2 - λX3 + λX4 при условиях 3X1 - 3X2 - X3 + X4 ≥ 5; 2X1 - 2X2 + X3 - X4 ≤ 3; Xk ≥ 0, k = 1 ... 4; -∞ < λ < ∞.
|
66. Что такое решение, оптимальное по Парето в многокритериальной задаче. Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето. 67. Объясните, почему метод ВИГ принадлежит к методам отсечения? Вообще, отсечение- отбрасывание части допустимой области. Применяется это тогда, когда нужно найти целочисленное решение. Метод ВИГ принадлежит к методам отсечения потому, что при решении задачи этим методом, допустимая область делится на части и при решении задачи для каждой отдельной части, мы оставшиеся части временно не учитываем( т.е. отсекаем).
68. Почему нельзя решать задачу целочисленного ЛП, решив ее сначала как обычную задачу ЛП без учета целочисленности, а затем округлив полученное решение? 1) Потому что не известно в какую сторону округлять( в большую или в меньшую) 2) Можно выйти за пределы допустимой области 3) Оптимальное целочисленное решение может быть не в соседней точке, а через одну, две, десять и т.д.
69. Что такое решение, оптимальное по Парето, в многокритериальной оптимизации? Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (стоимость, надежность и т.п.) Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето. Общий вид задачи многокритериальной оптимизации: fi(x) → max (i=1,2,…,n), x € D x- ? |
64. Приведите пример многокритериальной задачи z1= 4x1+10x2 → max z2=x1+x2 →max
x1, x2 € Z x1, x2 ≥0
x1,
x2
- ?
65. Сформулируйте условие окончания ветвления при решении задач методом ВИГ. Основная идея метода «ветвей и границ» состоит в разбиении множества допустимых решений на подмножества, которые, в свою очередь, разбиваются на подмножества и т.д. При этом среди возникающих подмножеств могут быть такие, которые не содержат допустимых решений или заведомо не содержат оптимальных решений. Если это удается определить на некотором этапе с помощью тех или иных оценок, то такие подмножества исключаются из дальнейшего рассмотрения. В результате решение находится частичным перебором. Критерии окончания ветвления: В задаче на максимум в начале решения граничное значение целевой функции, или рекорд, полается равным - ∞ . 1. Получена задача, не имеющая решения. Это становится все более вероятным с увеличением глубины ветвления, когда все большее число ограничений вида xi ≤ [{xi0] , или xi ≥ [{xi0] +1 добавляется к уже существующим ограничениям( так, что все более вероятным становится несовместимость системы ограничений получаемых задач). 2. Если находится новое целочисленное решение, то оно сравнивается с рекордом; если прежний рекорд превзойден, то запоминается новый рекорд, в противном случае остается старый. 3. Получаемое оптимальное нецелочисленное решение задачи на какой-то стадии ветвления сравнивается с рекордом; если это значение меньше, чем рекорд, то ветвление задачи прекращается, так как нет возможности побить рекорд. Непобитый рекорд дает оптимальное решение исходной задачи ЦЛП. 70. Описать метод ветвей и границ Основная идея метода «ветвей и границ» состоит в разбиении множества допустимых решений на подмножества, которые, в свою очередь, разбиваются на подмножества и т.д. При этом среди возникающих подмножеств могут быть такие, которые не содержат допустимых решений или заведомо не содержат оптимальных решений. Если это удается определить на некотором этапе с помощью тех или иных оценок, то такие подмножества исключаются из дальнейшего рассмотрения. В результате решение находится частичным перебором.
|
||||||||||||||||||||
|
71. Метод динамического программирования, функция состояния, уравнение Беллмана Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге. В основе динамического программирования лежат 2 принципа: Первый- принцип оптимальности Беллмана: каковы бы ни были начальное состояние системы и принятое решение, все последующие решения на остальных шагах должны составлять оптимальную стратегию относительно состояния, возникающего в результате первого решения. Второй- принцип вложения: природа задачи, допускающая использование метода динамического программирования, не меняется при изменении числа шагов. Структура процессов, исследуемых методом динамического программирования, должна удовлетворять следующим условиям:
Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления. |
72. Составить математическую модель и записать функциональное уравнение Беллмана (рекуррентное соотношение), расшифровать все переменные и функции, входящие в него для следующей задачи. F(x1, x2, x3, x4) =f1(x1) + f2(x2) + f3(x3) + f4(x4) x1+x2+x3+x4= Z(700) gk= max( fk(xk) + gk-1 (Z-xk)) F= g4(Z) xk= 0, 100, 200, 300, 400
g3(400) =105 |
77. В чем отличие «условий неопределенности» от «вероятностных условий». Что такое полная неопределенность и частичная неопределенность? Принять, выработать решение в условиях определенности- это фактически найти экстремум известной функции при установленных ограничениях. Когда же некоторые существенные обстоятельства принятия решений известны не полностью не полностью или случайны, то говорят, что решение принимается в условиях неопределенности. Иными словами, неопределенность- это отрицание определенности. Не все случайное можно измерить вероятностью. Неопределенность- более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик, отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Иначе говоря, уникальные единичные случайные явления связаны с неопределенностью, а массовые случайные явления обязательно допускают некоторые закономерности вероятностного характере. Предположим, что в рассматриваемой схеме известны вероятности pj того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью
|
||||||||||||||||||||
|
79. Как по платежной матрице составить матрицу рисков? П 5 2 8 4 Q= 2 3 4 12 8 5 3 10 1 4 2 8 Составим матрицу рисков. Имеем q1= max{qi1}=8, q2=5, q3=8, q4=12 С 3 3 0 8 R= 6 2 4 0 0 0 5 2 7 1 6 4
80. Как рекомендуется принять решение по «Вальду» Правило крайнего пессимизма. Рассматривая i-е решение, будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход ai
= minj{qij}.Но
теперь среди ai
выберем
i0-е
решение с наибольшим aij.
Итак, правило Вальда рекомендует
принять i0-е
решение, такое, что
81. Как рекомендуется принимать решение «по Сэвиджу»? Правило
минимального риска. При применении
этого правила анализируется матрица
рисков R=||
rij
||.
Рассматривавая i-е
решение, будем полагать, что на самом
деле складывается ситуация максимального
риска bi=
max{rij}.
Но теперь выберем i0-е
решение с наименьшим bi0.
Итак, Правило Севиджа рекомендует
принять i0-е
решение, такое, что
|
78. Что такое платежная матрица и матрица рисков, экономический смысл платежной матрицы Предположим, что ЛПР рассматривает несколько (i=1,…,m) возможных решений. Ситуация неопределенная, понятно лишь, что наличествует какой-то из вариантов j=1,…,n. Если будет принято i-е решение в j-й ситуации, то фирма, возглавляемая ЛПР, получит доход qij. Матрица Q=|| qij || называется матрицей последствий( возможных решений). Какое же решение нужно принять ЛПР? В ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме? Допустим, мы хотим оценить риск, который несет в себе i-е решение. Нам неизвестна реальная ситуация. Но если бы мы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход, в j-й ситуации было бы принято решение, дающее доход qj= max{qij}. Значит, принимая i-е решение, мы рискуем получить не qj, а только qij и недобрать rij=qj-qi. Матрица R=|| rij || называется матрицей рисков. |
82. Как рекомендуется принимать решение «по Гурвицу»? Взвешивающее
пессимистический и оптимистический
подходы к ситуации. Принимая i-е
решение, при котором достигается max
выбирается из субъективных соображений. Если ג →1, то правило Гурвица приблежается к правилу Вальда, при ג →0 правило Гурвица приблежается к правилу «розового оптимизма». 83. Что такое правило «розового оптимизма»? ( 0 6 5 2 ) ( 6 2 8 22) ( 9 4 3 32) ( -6 -4 -12 10) ЛПР считает, что для него сложится самая благоприятная ситуация, т.е. он получит самый большой доход в результате своей деятельности ci = max qij. Теперь выберем решение i0 с наибольшим ci0. Итак, правило “розового оптимизма рекомендует принять решение i0 такое, что ci0 = max (max qij). Так, в вышеуказанном примере имеем с1 = 6, с2 = 22, с3 = 32, с4 = 10. Теперь из чисел 6, 22, 32, 10 берем максимальное. Это — 32. Значит, правило “розового оптимизма” рекомендует 3-е решение.
84. Как находится риск финансовой операции как среднее квадратическое? Существует ещё одно понимание риска. Рассмотрим какую-либо операцию, доход которой есть случайная величина Q. Как мы знаем средний ожидаемый доход- математическое ожидание случайной величины MQ а вот среднее квадратическое отклонение (СКО) σQ=√DQ- это мера разброса возможных значений дохода вокруг среднего ожидаемого дохода mQ. Напомним что DQ=M(Q-MQ)².среднее квадратичное отклонение дохода от операции r1=√DQi в данном случае и будет служить определение меры риска. |
||||||||||||||||||||
|
85. Что такое доминирование финансовых операций? При расчете средних доходов и рисков, получаем средние ожидаемые доходы и риски и строим на графике( Q= q откладываем по горизонтали, а риск r- по вертикали.) Получили четыре точки. Чем правее расположена точка ( q, r), тем более доходной операции она соответствует, чем выше расположена точка- тем с большим риском связана эта операция. Значит нужно выбирать точку правее и ниже. Точка (q’, r’) доминирует точку (q, r) если q’ ≥ q и r’≤ r и хотя бы одно из этих неравенств строгое. Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек( операций) наз. множеством, оптимальным по Парето. 86. Что такое взвешивающая формула? Если из рассмотренных операций необходимо выбрать лучшую, то ее надо обязательно выбирать из операций, оптимальных по Парето. Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу. Для пар (q, r) данная формула дает одно число, по которому и определяют лучшую операцию. Пример использования взвешивающей формулы( пример задачи 10.3 стр 425 :-) ) : Пусть взвешивающая формула есть Φ(q, r)= q-r Вычисляем, получаем Φ(Q1)= 4.83-1.77= 3.064 ; Φ(Q2)= 0.6; Φ(Q3)= 4.7; Φ(Q4)= 0.27 и лучшей операцией оказывается третья. |
87. Каков экономический смысл среднего ожидаемого дохода финансовой операции? Формула для его расчета
При
многократном повторении всей ситуации,
котор. применяется в этой операции,
доход будет примерное равен рассчитанному
среднему.
88. Как рекомендуется принимать решение по критерию наибольшего среднего ожидаемого дохода? Правило максимизации среднего ожидаемого дохода.
Д qi1 … qin p1 … pn
Математическое ожидание MQi есть средний ожидаемый доход. Рассматриваемое правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход. |
89. Верхняя и нижняя цена игры в матричной игре в чистых стратегиях, их нахождение. Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока, очевидно, есть m чистых стратегий, у второго – n. При анализе игр противник считается сильным, т.е. разумным. Рассмотрим описанную конфликтную ситуацию с точки зрения первого игрока. Если мы( первый игрок) выбираем свою i-ю стратегию (i-ю строку матрицы А), то второй игрок, будучи разумным, выберет такую стратегию j, которая обеспечит ему наибольший выигрыш ( а нам наименьший), т.е. он выберет такой столбец j матрицы А, в котором платеж aij( второго игрока первому) минимален. Переберем все наши стратегии i= 1,2,,..,m и выберм ту из них, при которой второй игрок, действуя максимально разумно, заплатит нам наибольшую сумму. Величина α = maxi=1,2,…n minj=1,2,…m aij называется нижней ценой игры, а соответствующая ей стратегия первого игрока- максиминной. Аналогичный рассуждения( но уже с точки зрения второго игрока) определяют верхнюю цену игры β = minj=1,2,…n maxi=1,2,…m aij и соответствующую ей минимаксную стратегию второго игрока. По своему определению нижняя цена игры α представляет собой максимальный гарантированный выигрыш первого игрока( т.е. применяя свою максиминную стратегию, первый игрок обеспечивает себе выигрыш, не меньший α), а верхняя цена- величину, противоположную минимальному гарантированному проигрышу второго игрок( т.е. применяя свою минимаксную стратегию, второй игрок гарантивует, что он не проиграет больше, чем β ,или, иначе, выиграет не меньше , чем (-β)). 90. Оптимальные стратегии в матричной игре в чистых стратегиях, условие их существования, седловая точка матрицы. Если α= β, то говорят, что игра имеет седловую точку в чистых стратегиях. Общее значение α и β называется ценой игры и обозначается v= α= β . При этом стратегии игроков, соответствующие седлововой точке, называются оптимальными чистыми стратегиями, так как эти стратегии являются наиболее выгодными сразу для обоих игроков, обеспечивая первому игроку гарантированный выигрыш не менее v, а второму игроку- гарантированный проигрыш не более (-v), и отклоняться игрокам от этих стратегий невыгодно. |




 аждой
квадратной матрице А n-го
порядка можно поставить в соответствие
некоторое число, называемое определителем,
или детерминантом, n-го
порядка и обозначаемое det
A,
/A/
или
аждой
квадратной матрице А n-го
порядка можно поставить в соответствие
некоторое число, называемое определителем,
или детерминантом, n-го
порядка и обозначаемое det
A,
/A/
или
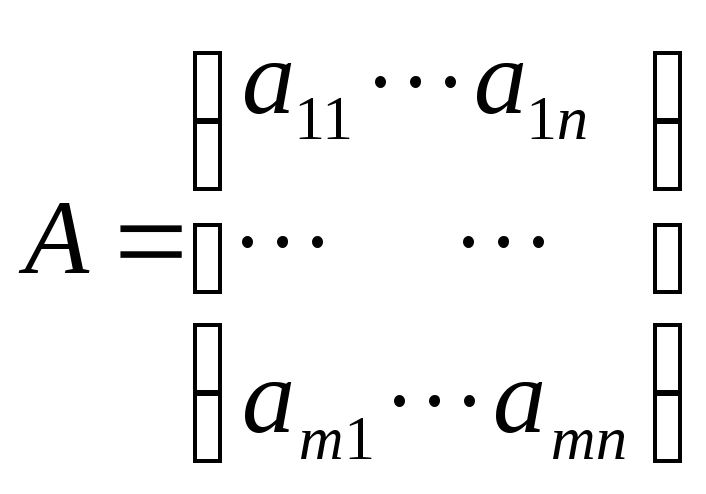 ,
,
 ,
,
 ри
ограничениях:
ри
ограничениях:



 (2)
(2) x1
+ g1,m+1xm+1
+
... + g1nxn
= h1,
x1
+ g1,m+1xm+1
+
... + g1nxn
= h1,
 x1
+ g1,m+1xm+1
+
... + g1nxn
= h1,
x1
+ g1,m+1xm+1
+
... + g1nxn
= h1,
 тсутствие
оптимального решения – неограниченность
целевой функции.
Х3
Х5
Х7
тсутствие
оптимального решения – неограниченность
целевой функции.
Х3
Х5
Х7 опустим
необходимо минимизировать целевую
функцию L=c1x1+c2x2+...cnxn
(1), при условиях:
опустим
необходимо минимизировать целевую
функцию L=c1x1+c2x2+...cnxn
(1), при условиях:
 (2)
(2) (4)
(4) (5)
(5) (2)
(2) (4)
(4) (5)
(5)

 3.
Составляется система ограничений
двойственной задачи, при этом матрица
из коэффициентов системы ограничений
исходной задачи транспонируется, знак
неравенства меняется на противоположный,
свободными членами будут являться
коэффициенты из целевой функции
исходной задачи:
3.
Составляется система ограничений
двойственной задачи, при этом матрица
из коэффициентов системы ограничений
исходной задачи транспонируется, знак
неравенства меняется на противоположный,
свободными членами будут являться
коэффициенты из целевой функции
исходной задачи: (2)
(2) i(x)
→max
(i= 1,2,…, n)
i(x)
→max
(i= 1,2,…, n) x1+2x2
≤
40
x1+2x2
≤
40
 усть
матрица последствий есть
усть
матрица последствий есть
 ледовательно,
матрица рисков
ледовательно,
матрица рисков
 Q1=∑Qi
* pi
,
p-
вероятность, q-
доходность
Q1=∑Qi
* pi
,
p-
вероятность, q-
доходность оход,
получаемый фирмой при реализации i-го
решения, является случайной величиной
Qi
с рядом распределения
оход,
получаемый фирмой при реализации i-го
решения, является случайной величиной
Qi
с рядом распределения