
- •Курсовая работа по дисциплине «Прикладная математика»
- •1. Линейная производственная задача
- •2. Двойственная задача
- •3. Задача о «расшивке узких мест производства»
- •4. Транспортная задача линейного программирования
- •5. Динамическое программирование. Распределение капитальных вложений
- •6. Матричная игра как модель конкуренции и сотрудничества
- •Найду решение игры в смешанных стратегиях.
- •Использованная литература:
Государственное образовательное учреждение
высшего профессионального образования
Государственный Университет Управления
Кафедра прикладной математики
Курсовая работа по дисциплине «Прикладная математика»
|
Выполнила |
Васильева Екатерина Игоревна |
|
Институт |
Бизнеса в Строительстве и Управления Проектом |
|
Специальность |
Менеджмент организации |
|
Вариант |
третий |
|
Отделение |
в/о |
|
Курс |
II |
|
Группа |
I |
|
Руководитель |
Багров А.П. |
|
Дата сдачи на проверку |
|
|
Дата защиты |
|
|
Оценка |
|
|
Подпись руководителя |
|
Москва 2004 г.
|
Оглавление | |
|
|
Стр. |
|
1. Линейная производственная задача……………………………..…… |
2 |
|
2. Двойственная задача………………………………………………..…. |
10 |
|
3. Задача о «расшивке узких мест производства»…………………..…. |
13 |
|
4. Транспортная задача линейного программирования……………...... рования………………………….. |
15 |
|
5. Динамическое программирование. Распределение капитальных вложений………………………………………………………..…………………………….. |
19 |
|
6. Матричная игра как модель конкуренции и сотрудничества…….… |
22 |
|
7. Матричная модель производственной программы предприятия…………………………………………………………………… |
26 |
|
8. Использованная литература…………………………………………... .…………………………………………….. |
28 |
|
|
|
1. Линейная производственная задача
Предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известны технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли.
Технологическая матрица A, в которой каждый элемент aij означает необходимое количество i-го ресурса для выпуска j-го вида продукции:


Вектор B объемов ресурсов, каждый элемент которого biозначает предельное количество i-го ресурса для выпуска всего объема продукции:


В ектор
удельной прибыли C, элементы которого
cj
означают прибыль от производства единицы
продукции j-го вида:
ектор
удельной прибыли C, элементы которого
cj
означают прибыль от производства единицы
продукции j-го вида:
С = ( 48 15 11 32 )
Количество каждого из товаров задаётся с помощью производственной программы:
 ,
где
,
где
x1, x2, x3, x4 - кол-во 1-ой, 2-ой, 3-ей и 4-ой продукции соответственно.
Технологическая матрица затрат показывает какое количество ресурсов требуется для производства 1 единицы продукции. Каждому виду продукции соответствует столбец в технологической матрице затрат А. Каждая строка матрицы А соответствует одному из видов ресурсов. Чтобы получить расход каждого ресурса при заданной производственной программе перемножим матрицу А и вектор производственной программы X:

Каждый элемент полученного вектора равен расходу соответствующего ресурса при заданной производственной программе, т.е. при x1, x2, x3, x4. Так как матрица А указывает на необходимое количество определённого ресурса для производства 1 единицы продукции, то умножая это число на общее количество продукции данного вида я получаю расход данного ресурса для производства заданного количества определённого вида продукции. Сложив расход ресурса по всем видам продукции, я получаю общий расход ресурса.
Вектор В указывает на располагаемое количество ресурсов. Каждый элемент соответствует одному виду ресурса.
Вектор С указывает на прибыль от продажи 1 единицы продукции каждого вида. Каждый элемент вектора соответствует одному виду продукции. Чтобы найти прибыль от каждого вида продукции следует помножить вектор производственной программу X на вектор удельной прибыли С:


С ложив
элементы полученного вектора я получаю
совокупную прибыль от продажи всей
продукции при заданном векторе
производственной программы X. Так как
x1,
x2,
x3,
x4
– неизвестные запишем полученное
выражение в виде функции:
ложив
элементы полученного вектора я получаю
совокупную прибыль от продажи всей
продукции при заданном векторе
производственной программы X. Так как
x1,
x2,
x3,
x4
– неизвестные запишем полученное
выражение в виде функции:
Z = 48x1 + 15x2 + 11x3 + 32x4
Для достижения максимальной прибыли требуется найти максимум полученной функции Z. При этом x1, x2, x3, x4 по смыслу 0. Учитывая условия ограничения по ресурсам, получаю задачу на условный экстремум:
Z
 =48x1
+ 15x2
+ 11x3
+ 32x4
max
=48x1
+ 15x2
+ 11x3
+ 32x4
max


x 1
0, x2
0, x3
0,
x4
0,
x5
0,
x6
0,
x7
0
1
0, x2
0, x3
0,
x4
0,
x5
0,
x6
0,
x7
0
Для ее решения систему неравенств при помощи дополнительных неизвестных х5, х6, х7 заменю системой линейных алгебраических уравнений
Z
 =48x1
+ 15x2
+ 11x3
+ 32x4
max
=48x1
+ 15x2
+ 11x3
+ 32x4
max
x 1
0, x2
0, x3
0,
x4
0,
x5
0,
x6
0,
x7
0
1
0, x2
0, x3
0,
x4
0,
x5
0,
x6
0,
x7
0
где дополнительные переменные имеют смысл остатков соответствующих ресурсов, а именно
х5 – остаток ресурса 1-го вида,
х6 – остаток ресурса 2-го вида,
х7 – остаток ресурса 3-го вида.
Решаю полученную задачу симплексным методом (методом направленного перебора базисных допустимых решений):
Я воспользуюсь тем, что правые части всех
уравнений системы (6) неотрицательны, а
сама система имеет предпочитаемый вид
– дополнительные переменные являются
базисными. Приравняв к нулю свободные
переменныеx1,
x2,
x3,
x4
получаю базисное неотрицательное
решение
воспользуюсь тем, что правые части всех
уравнений системы (6) неотрицательны, а
сама система имеет предпочитаемый вид
– дополнительные переменные являются
базисными. Приравняв к нулю свободные
переменныеx1,
x2,
x3,
x4
получаю базисное неотрицательное
решение
x1=0, x2=0, x3=0, x4=0, x5=0, x6=0, x7=0
п ервые
компоненты которого определяют
производственную программу
ервые
компоненты которого определяют
производственную программу
x1=0, x2=0, x3=0, x4=0
Из выражения (3) видно, что наиболее выгодно начинать производить продукцию 1-го вида. Чем больше выпуск этой продукции, тем больше прибыль. Я выясню, до каких пор мои ресурсы позволяют увеличить выпуск этой продукции.
Общее решение для системы уравнений (6)
X 5
= 116 - 4x1
- 2x2
- 3x3
- x4
5
= 116 - 4x1
- 2x2
- 3x3
- x4
X6 = 94 - 2x1 - 3x3 - 2x4
X7 = 196 - 4x1 - x2 - 5x4
Я пока сохраняю в общем решении x2=0, x3=0, x4=0 и увеличиваю только x1. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств

Я даюx1
наименьшее значение
x1=
29, которое оно может принять при нулевых
значениях других свободных неизвестных,
и подставлю его в (10). Получаю для системы
уравнений (6) частное неотрицательное
решение
даюx1
наименьшее значение
x1=
29, которое оно может принять при нулевых
значениях других свободных неизвестных,
и подставлю его в (10). Получаю для системы
уравнений (6) частное неотрицательное
решение
x1=29, x2=0, x3=0, x4=0, x5=0, x6=36, x7=80
Э то
решение является новымбазисным
неотрицательным
решением системы алгебраических
уравнений (6), для получения которого
достаточно было принять в системе (6)
неизвестную x1
за разрешающую и
перейти к новому предпочитаемому виду
этой системы, сохранив правые части
уравнений неотрицательными, для чего
за разрешающее уравнение я обязана
принять первое, т.к.
то
решение является новымбазисным
неотрицательным
решением системы алгебраических
уравнений (6), для получения которого
достаточно было принять в системе (6)
неизвестную x1
за разрешающую и
перейти к новому предпочитаемому виду
этой системы, сохранив правые части
уравнений неотрицательными, для чего
за разрешающее уравнение я обязана
принять первое, т.к.
а разрешающим элементом будет a11 = 4.
Применяя известные формулы исключения, получаю для системы уравнений (6) новый предпочитаемый эквивалент

П риравняв
к нулю свободные переменныеx2,
x3,
x4,
x5
получаем базисное неотрицательное
решение, совпадающее с (11), причем первые
четыре компоненты его определяют новую
производственную программу
риравняв
к нулю свободные переменныеx2,
x3,
x4,
x5
получаем базисное неотрицательное
решение, совпадающее с (11), причем первые
четыре компоненты его определяют новую
производственную программу
x1=116/4, x2=0, x3=0, x4=0, x5=0
Я исследую, является ли эта программа наилучшей, т.е. обеспечивает ли она наибольшую прибыль. Для этого я выражу функцию прибыли (3) через новые свободные переменные x2, x3, x4, x5. Из уравнения системы (12) выражаю базисную переменную x1 через свободные и подставляю в (3).
Z = 1392 + 48 (116/4 - 1/2 x2 – 3/4 x3- 1/4 x4 – 1/4 x5) + 15x2 + 11x3 + 32 x4
Z = 1392 –
24 x2 –
36 x3 –
12 x4 –
12 x5 +
15 x2 +
11 x3 +
32 x4
= 1392 –
24 x2 –
36 x3 –
12 x4 –
12 x5 +
15 x2 +
11 x3 +
32 x4
Z = 1392 - 9 x2 - 25 x3 + 20 x4 - 12 x5
И з
этого выражения видно, что программа
(13) не является оптимальной и что прибыль
будет расти наиболее быстро при увеличении
количестваx4четвертой продукции. Поэтому я принимаюx4 в системе (12) за
разрешающую неизвестную, нахожу
разрешающее уравнение по
з
этого выражения видно, что программа
(13) не является оптимальной и что прибыль
будет расти наиболее быстро при увеличении
количестваx4четвертой продукции. Поэтому я принимаюx4 в системе (12) за
разрешающую неизвестную, нахожу
разрешающее уравнение по

и исключаю x4 из всех уравнений системы (12), кроме 3-го уравнения. Получаю следующий предпочитаемый эквивалент системы условий, который определит для системы (6) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого мне придется выразить функцию (14) через новые свободные переменные, удалив оттуда переменнуюx4, ставшую базисной.
Я обращаю внимание на то, что эти удаления
можно выполнить очень просто. Я представлю
соотношение (3) в виде уравнения
обращаю внимание на то, что эти удаления
можно выполнить очень просто. Я представлю
соотношение (3) в виде уравнения
- 48 x1 – 15 x2 – 11 x3 – 32 x4 = 0 - Z
и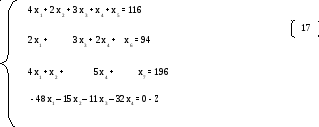 припишу его к системе (6). Получается
вспомогательная система уравнений
припишу его к системе (6). Получается
вспомогательная система уравнений
x 1
– в системе (6)
разрешающая неизвестная, этой переменной
в последнем уравнении системы (17) отвечает
наименьший отрицательный коэффициент
1 =
- 48.
1
– в системе (6)
разрешающая неизвестная, этой переменной
в последнем уравнении системы (17) отвечает
наименьший отрицательный коэффициент
1 =
- 48.
a 11
= 4 – разрешающий
элемент. Т.к. я исключила неизвестную
переменную x1 из
всех уравнений системы (6), кроме 1-го, и
из функции (3), очевидно стало видно, что
достаточно умножить 1-е уравнение системы
(17) на 12 и прибавить к 4-му; получу
11
= 4 – разрешающий
элемент. Т.к. я исключила неизвестную
переменную x1 из
всех уравнений системы (6), кроме 1-го, и
из функции (3), очевидно стало видно, что
достаточно умножить 1-е уравнение системы
(17) на 12 и прибавить к 4-му; получу
9 x2 + 25 x3 - 20 x4 + 12 x5 = 1392 - Z
Таким образом, я преобразовала вспомогательную систему уравнений (17) к виду


П ервые
3-и уравнения этой системы представляют
некоторый предпочитаемый эквивалент
(12) системы уравнений (6) и определяют
базисное неотрицательное решение (11) и
производственную программу (13), а из
последнего уравнения системы (19)
получается выражение (14) функции цели
через свободные переменные. Очевидно,
если имеется хотя бы один отрицательный
коэффициент j
при какой-нибудь
переменной xj
в последнем уравнении системы (19), то
производственная программа не является
наилучшей и можно далее продолжать
процесс ее улучшения. С помощью (14) я
выяснила, что следует начинать производить
продукцию 4-го вида, т.е. фактически я
нашла в последнем уравнении системы
(19) наименьший отрицательный коэффициент
ервые
3-и уравнения этой системы представляют
некоторый предпочитаемый эквивалент
(12) системы уравнений (6) и определяют
базисное неотрицательное решение (11) и
производственную программу (13), а из
последнего уравнения системы (19)
получается выражение (14) функции цели
через свободные переменные. Очевидно,
если имеется хотя бы один отрицательный
коэффициент j
при какой-нибудь
переменной xj
в последнем уравнении системы (19), то
производственная программа не является
наилучшей и можно далее продолжать
процесс ее улучшения. С помощью (14) я
выяснила, что следует начинать производить
продукцию 4-го вида, т.е. фактически я
нашла в последнем уравнении системы
(19) наименьший отрицательный коэффициент
m

 in
(j
0) =
-
20
= 1
in
(j
0) =
-
20
= 1
и решила перевести свободную переменную x3 в число базисных, для чего, согласно (15) определила разрешающее уравнение и указала разрешающий элемент
a24 = 4
Преобразую всю вспомогательную систему (19) по формулам исключения. Эта система преобразуется к виду


П ервые
3-и системы уравнения (20) представляют
некоторый предпочитаемый эквивалент
системы уравнений (6) и определяют
базисное неотрицательное решение
системы условий рассматриваемой задачи
ервые
3-и системы уравнения (20) представляют
некоторый предпочитаемый эквивалент
системы уравнений (6) и определяют
базисное неотрицательное решение
системы условий рассматриваемой задачи
x1=24, x2=0, x3=0, x4=80, x5=0, x6=6, x7=0,
т .е.
определяют производственную программу
.е.
определяют производственную программу
x1=24, x2=0, x3=0, x4=80
и остатки ресурсов:
п ервого
видаx5=0
ервого
видаx5=0
второго вида x6=6
третьего вида x7=0
В последнем уравнении системы (20) среди
коэффициентов при неизвестных в левой
части уравнения нет ни одного
отрицательного. Если из этого уравнения
выразить функцию целиZ
через остальные неотрицательные
переменные
последнем уравнении системы (20) среди
коэффициентов при неизвестных в левой
части уравнения нет ни одного
отрицательного. Если из этого уравнения
выразить функцию целиZ
через остальные неотрицательные
переменные
Z = 1792 - 4 x2 - 10 x3 - 7 x5 - 5 x7,
т
 о
становиться совершенно очевидным (в
силу того, что всеxj
0), что прибыль будет
наибольшей тогда, когда
о
становиться совершенно очевидным (в
силу того, что всеxj
0), что прибыль будет
наибольшей тогда, когда
x2=0, x3=0, x5=0, x7=0.
Э то
означает, что производственная программа
(22) является наилучшей и обеспечивает
предприятию наибольшую прибыль
то
означает, что производственная программа
(22) является наилучшей и обеспечивает
предприятию наибольшую прибыль
Zmax=1792
|
С |
Базис |
Н |
48 |
15 |
11 |
32 |
0 |
0 |
0 |
Пояснения
|
|
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 | ||||
|
0 0 0
|
X5 X6 X7 Z0-Z |
116 94 196 0-Z |
4 2 4 -48 |
2 0 1 -15 |
3 3 0 -11 |
1 2 5 -32 |
1 0 0 0 |
0 1 0 0 |
0 0 1 0 |
j
|
|
0 0 48 |
X6 X7 X1 Z0-Z |
36 80 116/4 1392-Z |
0 0 1 0 |
-1 -1 1/2 9 |
3/2 -3 3/4 25 |
3/2 4 1/4 -20 |
-1/2 -1 1/4 12 |
1 0 0 0 |
0 1 0 0 |
min (116/4:1/4, 36:3/2, 80:4)= 80/4
min = -20 |
|
32 0 48 |
X4 X6 X1 Z0-Z |
20 6 24 1792-Z |
0 0 1 0 |
-1/4 - 5/8 9/16 4 |
-3/4 21/8 15/16 10 |
1 0 0 0 |
-1/4 - 1/8 5/16 7 |
0 1 0 0 |
1/4 - 3/8 -1/16 5 |
все
j
|
Проверим получившийся результат.
В оспользуюсь
тем, что в оптимальной производственной
программеx2 = 0 иx3 = 0.Предположу,
что вторую и третью продукции я не
намеревалась выпускать с самого начала.
Рассмотрю задачу с оставшимися двумя
переменными.Математическая
модель будет выглядеть следующим
образом:
оспользуюсь
тем, что в оптимальной производственной
программеx2 = 0 иx3 = 0.Предположу,
что вторую и третью продукции я не
намеревалась выпускать с самого начала.
Рассмотрю задачу с оставшимися двумя
переменными.Математическая
модель будет выглядеть следующим
образом:
X (x1, x4) - ?
Z = 48x1
+ 32x4
max
= 48x1
+ 32x4
max
4 x1+ 1x4116
2 x1+ 2x494
4 x1+ 5x4196
x1 0, x4 0
Следует при этом обратить внимание на то, что последовательно улучшение программы
(
 x1=0,
x4=0)
(x1=116/4,
x4=0)
(x1=24,
x4=20)
x1=0,
x4=0)
(x1=116/4,
x4=0)
(x1=24,
x4=20)
на графике означает движение от одной вершины многогранника допускаемых решений к другой вершине по связывающей их стороне многоугольника.
Графическое решение этой задачи представлено на Рис. 1.
Из графика видно, что результаты совпадают.
Обращенный базис, отвечающий оптимальной производственной программе, содержится в последней симплексной таблице:
О бращенный
базисQ-1
бращенный
базисQ-1
-1/4 0 1/4
Q-1= - 1/8 1 - 3/8
5/16 0 -1/16
х5 х6 х7
Для того, чтобы убедиться в правильности полученного решения, следует проверить отношение Н = Q-1 * В:
Самопроверка.

 -1/4•116+0•94+1/4•196
20
-1/4•116+0•94+1/4•196
20
Q-1 •B= -1/8•116+1•94-3/8•196 = 6 =H
5/16•116+0•94-1/16•196 24

 = 1,n
= 1,n
