§ 3.6. The First Remarkable Limit and Its Generalization

The following limit exists and equals 1:

.

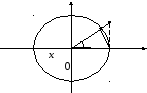
Proof. Take the circle centered at the origin of an arbitrary radius R. Clearly,

у М В А х	. Let us find the areas: , ,

. Substituting them into the inequalities and reducing by , we obtain

.

Let us divide these inequalities by sin x>0:

.

Replacing the ratios in the inequalities by the reciprocals and reversing the signs, we obtain

, or ,

whence

.

By Theorem IV, (3), the required limit exists:

.

Example:

(1) ,

2) .

3.6.1 The first generalized remarkable limit. The first remarkable limit can be generalized, namely, written in the more general form

(4)

In this formula, (х) is an infinitesimal; it is very important that the argument of the sine and the denominator must be absolutely identical.

Examples.

(1) ,

(2) .

§ 3.7. The Second Remarkable Limit

Consider the limit

. (5)

Theorem. The limit (5) exists and equals a number е between 2 and 3.

Scheme of the proof. Consider the value for a particular n. Decomposing it by the Binomial theorem, we see that this value increases with n.

After analyzing each term in the decomposition and using a geometric series, we show that this quantity is never larger than 3, i.e., b) the sequence is bounded. Theorem V of bounded increasing functions implies the existence of limit (5). See popular text-books for more details.

Consider the limit of the function

, (*)

where х is a real number.

Find a large number n for which n<x<n+1, we transform the expression and add 1:

, .

We raise the larger term to a larger power, the middle term to a middle power, and the smaller term to a lower power:

.

Let us find the limits of each term in the inequalities on by using (5):

,

.

Thus, the inequalities take the form , which cannot be true. This implies that the inequalities, and ( * ).

Now, let us prove that

. (**)

We use the substitution

, , ,

It yields limit (*), which was found above.

The following relation also holds:

,

this is proved by using the substitution x=–(t+1).

The number е satisfies the inequalities 2<e<3, e is an abbreviation for exponentials, i.e., «outer»; it is sometimes denoted by e=exp and approximately equals e2,71828.

y=e^x is the exponential function.

The formula

,

for changing the base of a logarithm implies a formula for the natural logarithm:

.

Examples. Find the following limits by using the second remarkable limit:

(1) ,

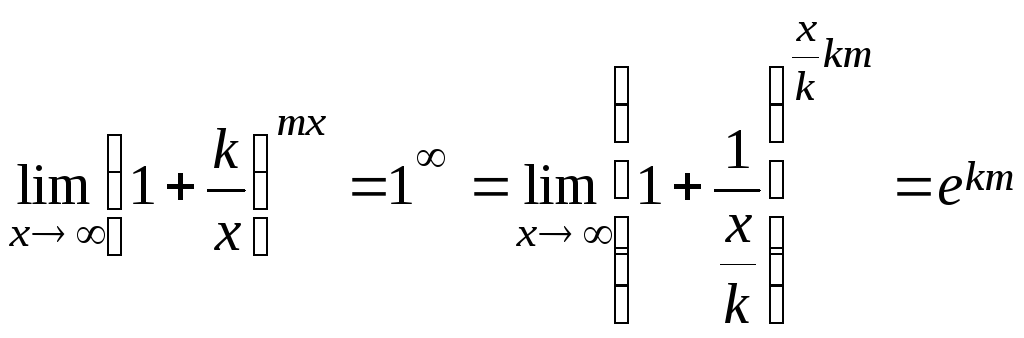(2)

(we separate out 1 parentheses)

.

§ 3.8. The Second Generalized Remarkable Limit

The second remarkable limit (*) and its modification (**) can be generalized, i.e., written in the more general forms

and

. (6)

In these formulas, (х) is an infinitesimal and N(x) is an infinitude. It is very important that in these formulas, N(x) and (х) are absolutely identical in the denominators and exponents.

For example,

(1) ,

(2) .

(3)